Essays, Posts & Presentations

1 Circuit Economy

Lester Telser

Author

Lester Telser

Title

1 Circuit Economy

Description

The more homogenous the productive enterprises in a economy the bigger the total output

1. Introduction

Few transactions in an economy resemble those that take place on an organized exchange, Yet the latter dominates what is taught in beginning economics. This explains mistaken views about the economy held by many ‘free market’ proponents. Their image of the economy distorts reality. Not exempt from these critical remarks are even some famous economists, Carl Menger, F. Y. Edgeworth and notably Friedrich A. Hayek whose influential The Road to Serfdom heads the list. My essay uses circuits to understand the actual economy as a correction to these mistaken views.

A circuit is a geometric entity in an economy regarded as a polygon with m vertexes. Its vertexes represent the individuals in an economy. The m-polygon is the framework for many networks made of related circuits. Their vertexes are connected by one-way way arrows. The arrows represent relations between the individuals who form circuits for their various purposes. An individual may belong to many circuits.

This formal structure is amenable to a mathematical apparatus that produces new results applicable to an economy. The following pentagon and its arrows can better illustrate than can a verbal description some properties of a circuit core model.

Out[]=

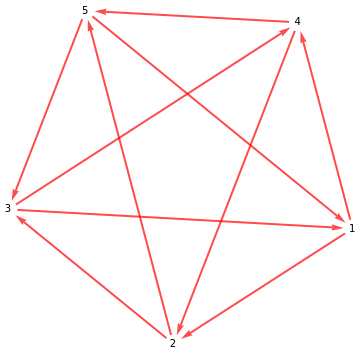
Graph of Pentagon

Next are 10 one-way arrows in the pentagon that connect selected vertexes.

Out[]=

{12,14,23,25,31,34,42,45,51,53}

They form 12 simple circuits. There are 5 circuits with 3 arrows in each, 5 circuits with 4 arrows in each and 2 circuits each with 5 arrows. The latter two 5 circuits include all 10 arrows.

Out[]//MatrixForm=

{34,45,53}

{23,34,42}

{14,45,51}

{12,25,51}

{12,23,31}

{25,53,34,42}

{14,45,53,31}

{14,42,25,51}

{14,42,23,31}

{12,25,53,31}

{14,42,25,53,31}

{12,23,34,45,51}

The model contains simple and super circuits, the former are either independent or are inside the latter. A simple circuit is made of one-way arrows each used only once. It has at least 3 one-way arrows and at most m. A tournament with m contestants offers an application of a circuit model. Contestants are represented by the vertexes of an m-polygon. Entries in the matrix mXm T[m] record the results of the contests. If contestant i beats contestant j, then entry (i,j) in the matrix equals 1 and entry (j,i) equals -1since contestant j loses to contestant i. The diagonal entries are 0. In a fair tournament the sum of the row and column entries are 0. Because a fair tournament contains the maximum number of simple circuits, it is the candidate I prefer for my circuit models.

A remarkable algebra, I call the Nöther algebra, has a collection of special matrics that represent an arrow in a circuit. These matrices multiplied together in the order specified by their relative order in the circuit represent the circuits that become manageable by virtue of the algebra.

A circuit model of an economy unveils a surprising paradox. It describes an economy by a collection of related circuits with production functions linear in the logs of their inputs and outputs. For each circuit and given the means of inputs, total outputs are bigger, the closer together their inputs. Total output of every circuit would be maximal when all their inputs were equally productive. This result applies especially within circuits. It does not follow there is a tendency toward a uniform distribution of circuit values.

2. Structure of a Simple Circuit Made of One-Way Arrows

An arrow in a fair odd m-polygon is described by a pair of integers [i,j], the source vertex i and destination vertex j. An arrow has another description owing to its position in a simple circuit. A simple s-circuit has s arrows arranged in a prescribed relative order. Each arrow in the circuit has an mXm arrow-matric G[i,j] whose terms all equal 0 except the term in row i, column j equals 1. Super circuits have similar collections of these matrices that describe their structure manageably.

Let θ[s,m] denote a simple s-circuit with s 1-way arrows whose coordinates are selected non zero terms from the mXm adjacency matrix A[m]. The adjacency matrix A[m] is a submatrix of the nonnegative terms in the tournament matrix T[m]. In A[m] arrow a[i,j] connects vertex i to vertex j, i



j.(1) θ[s,m] = {a[

], a[

], … , a[

s-1

]} .Each arrow a[

] has a Nöther matric denoted G[i,j]. Let H[s,m] denote the circuit-matric for θ[s,m]. Nöther algebra says(2) H[s,m]=

∏G[i,j]

, a[i,j] ∈ θ[s,m]H[s,m] is a diagonal matric. Its diagonal term is the product of its arrow-matrics in the prescribed relative order of the circuit arrows. Its only non zero term is in row [

], column [

] of H[s,m].

Let1+

i,j

denotethevalueofarrowa[i,j].Thevalueofthe3-circuit,V[θ],is(3)V[θ]=(1+

)(1+

)=1+

3. Maximum Maximorum

A famous theorem now enters the story with an important result for a circuit core model. The Theorem says that the arithmetic mean of a finite sample of positive numbers is greater than or equal to the geometric mean of this numbers. This result also holds for weighted means as follows.

∑

i=1

≥

∏

i=1

,1≥

>0,

∑

i=1

=1,&

>0.

Iuseasimplerlesscumbersomeformwith

=1/n.Thismakes'unweighted'means.

Theorem. If

> 0, then (Π

1/n

)

≤ (Σ

)/n =

.Proof. The maximum of Π

.(1) Π

≤

implies(2) (Π

1/n

)

≤

(Σ

)/n 

Let

denote the value of arrow i in an n-circuit of a fair m-polygon. Each

≥1

. The value of circuit θ, V(θ), is (3) V(θ) = Π

.Equation (2) says the geometric mean, GM(θ), does not exceed the arithmetic mean, AM(θ), of the arrow values.(4) GM(θ) = V(θ)

1/n

≤ (Σ

)/n = AM(θ)The gap between the two is minimal for that circuit where the return to each person equals the arithmetic mean.

The arithmetic mean of the value of the arrows in a circuit exceeds the geometric mean of their values unless

=ρ. Given the mean, the geometric mean varies inversely with the dispersion of its terms. The closer together are

i,j

, the closer is the geometric mean to the arithmetic mean. Given the arithmetic mean, the more nearly equal are the (1+

i,j

) in the circuit, the bigger the circuit value. This becomes important later.

4. Implications for a Core

For

≥ 0,(1)

(1+

) <

(1+

).The subscript identifies the arrow’s owner. Let

denote the return to owner i, i = 1, 2, … , n, n = m(m-1)/2.Let V(θ) in (2) denote the value of circuit θ .(2) V(θ) =

(1 +

).The core constraint is inequality (3)(3)

∑

iϵθ

≥ V(θ)If

=1+

, then the minimal payoff acceptable to owner i cannot satisfy (3) because of inequality (1). Therefore, the core constraints are not feasible. Changing to logs eliminates this obstacle. Instead of

, the owner of vertex i gets log

. The log of the value replaces the value. Instead of (3), we now have(4)

∑

iϵθ

log

≥ log V(γ) = log

iϵθ

(1 +

∑

iϵθ

log(1+

)

.Log

can satisfy (4) with equality even if some

=0. Arrows with ρ = 0 are unproductive so their value =1 and log 1 = 0.

The usual obstacle to a non empty core is conflict between the global optimum and a local optimum. The global optimum does not ensure that everyone is better off since there can be alternatives that the global optimum cannot dominate. This can happen in a circuit core model only when arrow contributions depend on circuit membership.Lemma. If the productivity of an arrow were the same in every circuit, then the optimal partition would satisfy all the core constraints in logs, 3.4 (5)- (7). When arrow productivity depends on circuit, the core could be empty.

Core constraints must reckon with the fact that the value of the s-circuit,

v[θ(s)]is

∏

i=1

x[i]&

1/s

∏

i=1

x[i]

≤

∑

1=1

x[i]s=

,sothat

∏

i=1

x[i]≤

∑

i=1

x[i]s

]

There is equality if and only if x[i] equals the arithmetic mean. The circuit value depends on the dispersion of the contributions of circuit members, holding constant the mean contribution. This creates an incentive for circuit members to reduce dispersion. An economy would tend to homogeneity within circuits but heterogeneity among circuits. These are disruptive forces.

Empirical Implications

Most nations have relatively homogenous populations constituting more than one half of a well-defined ethnic, racial and religious group. It would have been accurate to say this also for the U.S. until recently. Now the predominant group in the U.S. accounts for a little less than half its population. This makes the U.S. unique among the nations in the world. Switzerland, Belgium and Canada are close rivals for this class but their diverse groups are nearly self governing political states. Only Western nations such as England, France and the Netherlands that in the recent past had colonial empires now resemble the U.S. with respect to their heterogeneity on account of immigration from some of their former colonies. It is residential data for the U.S. that especially deserves attention as empirical confirmation of the circuit model. In the U.S. within urban residential neighborhoods there tends to be homogeneity but across neighborhoods heterogeneity prevails.

A circuit model deserves attention as a tool to analyze U.S. politics. Because simple circuits are likely to be relatively homogeneous, they can describe sparsely populated states; Montana, Wyoming and North Dakota. Super circuits apply to states with large urban centers; California, Ohio, Texas, New York, Ohio, Pennsylvania. Illinois, Georgia, Michigan, Wisconsin also fit as super circuits.

The Main Partition in a fair composite m-polygon has both relatively prime and relatively composite bands. Composite bands break up and some of their simple circuits join relatively prime bands to form super circuits. Such super circuits can represent a state with severable sizable urban concentrations.

* I have since learned that my matrixes are a special case of a total matric algebra. The square arrow-matrix G[i,j] that represents the arrow a[i,j] belongs to the total matric algebra of certain square matrixes (Birkhoff and MacLane, 1953, p. 240). They write multiplication of their matrixes

and

if j≠k. It is a feature of a complete matrix ring in van der Waerden (1950, Vol II, pp. 133 ff). His two volume treatise, first published in German in 1931, is based on lectures by Nöther and Artin. Both left Germany early in the Nazi period having been fired from their positions at Göttingen University. Nöther and Weyl are famous students of David Hilbert. MacLane wrote his doctoral dissertation under supervision by Weyl and was a student of Nöther.

Appendix

Although the matrixes are simple they may be unfamiliar to most readers. The adjacency matrix for the fair pentagon is A[5]

A[5]=

0	a[1,2]	0	a[1,4]	0
0	0	a[2,3]	0	a[2,5]
a[3,1]	0	0	a[3,4]	0
0	a[4,2]	0	0	a[4,5]
a[5,1]	0	a[5,3]	0	0

The terms parallel to the main diagonal are its two bands as follows.

band1	a[1,2]	a[2,3]	a[3,4]	a[4,5]	a[5,1]
band3	a[1,4]	a[2,5]	a[3,1]	a[4,2]	a[5,3]

A permutation matrix gives the coordinates of the arrows in the band but not their relative positions for the circuits they include with one exception, the first band shows the perimeter of the pentagon. Hence consider the permutation matrix for band 3 instead P[3]

P[3]

0	0	0	a[1,4]	0
0	0	0	0	a[2,5]
a[3,1]	0	0	0	0
0	a[4,2]	0	0	0
0	0	a[5,3]	0	0

Each arrow has its own Noether matric. Since there are 5 arrows, there are 5 Noether matrics.

In[]:=

G[1,5]:={{0,0,0,a[1,4],0},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0}}

G[2,5]:={{0,0,0,0,0},{0,0,0,0,a[2,5]},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0}}

G[3,1]:={{a[3,1],0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0}}

G[4,2]:={{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,a[4,2],0,0,0},{0,0,0,0,0}}

G[5,3]:={{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,0,a[5,3],0,0}}

The product of these 5 matrics is

a[1,4].a[4,2].a[2,5].a[5,3].a[3,1]	0	0	0	0
0	0	0	0	0
0	0	0	0	0
0	0	0	0	0
0	0	0	0	0

The term in row 1, col 1 gives the product of the arrows in the correct relative order of the circuit in band 3.The product of any other order would be zero.

References

Birkhoff, Garrett and Saunders Mac Lane. 1953 revised ed. A Survey of Modern Algebra. New York: Macmillan.Telser, Lester G. 1967. A Critique of Some Recent Research on the Explanation of the Term Structure of Interest Rates. Journal of Political Economy. 75: 546-61.van der Waerden, B. L. 1950. Modern Algebra. Vol II. Translated from the second revised German edition by Theodore J. Benac. New York: Frederick Ungar Publishing Co.. Weyl, Hermann. 1946. The Classical Groups; Their invariants and Representations. 2nd edition. Princeton: Princeton University Press.

Program



In[]:=

makeA[5]

In[]:=

pen:=makeGrph[A,3]

In[]:=

pen

Out[]=

In[]:=

Apply[DirectedEdge,arrw,1]

Out[]=

{12,14,23,25,31,34,42,45,51,53}

In[]:=

MatrixForm[findAllCycles[A]]

Out[]//MatrixForm=

{34,45,53}

{23,34,42}

{14,45,51}

{12,25,51}

{12,23,31}

{25,53,34,42}

{14,45,53,31}

{14,42,25,51}

{14,42,23,31}

{12,25,53,31}

{14,42,25,53,31}

{12,23,34,45,51}

Cite this as: Lester Telser, "1 Circuit Economy" from the Notebook Archive (2021), https://notebookarchive.org/2021-02-7vi864a