Essays, Posts & Presentations

A Computational Method to Predict X-ray Diffraction (XRD) Patterns

Hamza Alsamraee

Author

Hamza Alsamraee

Title

A Computational Method to Predict X-ray Diffraction (XRD) Patterns

Description

A Computational Method to Predict X-ray Diffraction (XRD) Patterns

Hamza Alsamraee

Mentor: Eryn Gillam

Description

XRD has been instrumental to the advancement of many fields in both science and technology. Each distinct lattice structure has its own XRD fingerprint, which scientists use to determine the chemical makeup of the lattice and in turn its physical properties. In this project, a large mathematical framework was utilized to effectively predict XRD patterns produced by various cubic lattice structures. First, the Bragg peak positions were computed from Bragg’s law with high accuracy. Structure factor was also computed for both unary and binary systems and used to compute intensity alongside plane multiplicity. High accuracy was found for unary systems, but binary systems showed less accurate predictions.

Getting the Bragg Peak Positions

Some Data

Importing the lattice constant and structure data

In[]:=

rawdata=Import["C:\\Users\\hamza\\Desktop\\project\\lattice data.xlsx","Data"];

Establishing column names and deleting extraneous columns

In[]:=

latticeAssoc=Function[u,<|"Compound"u〚1〛,"LatticeConstant"ToExpression[u〚2〛],"Structure"u〚3〛|>]/@First[rawdata]〚All,1;;3〛;

Making a dataset

In[]:=

latticeDataset=Dataset[latticeAssoc]

Out[]=

Compound	LatticeConstant	Structure
AlAs	5.6605	face-centered cubic
AlP	5.451	face-centered cubic
AlSb	6.1355	face-centered cubic
GaP	5.4505	face-centered cubic
GaAs	5.653	face-centered cubic
GaSb	6.0959	face-centered cubic
InP	5.869	face-centered cubic
InAs	6.0583	face-centered cubic
InSb	6.479	face-centered cubic
MgO	4.212	face-centered cubic
CdS	5.832	face-centered cubic
CdSe	6.05	face-centered cubic
CdTe	6.482	face-centered cubic
ZnO	4.58	face-centered cubic
ZnS	5.42	face-centered cubic
PbS	5.9362	face-centered cubic
PbTe	6.462	face-centered cubic
BN	3.615	face-centered cubic
BP	4.538	face-centered cubic
LiF	4.03	face-centered cubic
showing 1–20 of 43

“toCompound” converts a cation/anion pair to a compound, so it is compatible with the above dataset. It takes off the last two characters (indicating charge) and joins cation/anion to make the name of a compound

In[]:=

toCompound[list_]:=StringJoin[StringDrop[#,-2]&/@list]

Bragg’s Law

Given a d spacing value and a wavelength, this function gives back the Bragg peak positions

theta[d_,w_]:=2ArcSin[(w/(2d))]

Allowed Reflections

For different structures, certain planes have no contribution to peak intensity. For a body centered cubic unit cell, the total of h+k+l (Miller indices) has to be even to have a nonzero structure factor. For a face centered cubic unit cell, the parity of the Miller indices has to all be the same. To test for the same parity, an EvenQ function was mapped to the list of Miller indices; if they are all the same parity, there will be only one list element after deleting duplicates.

In[]:=

reflections[list_,n_]:=Drop[If[Length@list1,(If[ElementData[First@list,"CrystalStructure"]["Name"]=="body-centered cubic",Select[Flatten[Table[{h,k,l},{h,0,n},{k,0,n},{l,0,n}],2],EvenQ[Total[#]]&],If[ElementData[First@list,"CrystalStructure"]["Name"]=="face-centered cubic",Select[Flatten[Table[{h,k,l},{h,0,n},{k,0,n},{l,0,n}],2],Length@DeleteDuplicates[EvenQ/@#]1&],{}],{}]),If[Length@list2,(If[First@Normal[latticeDataset[Select[#CompoundtoCompound[list]&],"Structure"]]=="body-centered cubic",Select[Flatten[Table[{h,k,l},{h,0,n},{k,0,n},{l,0,n}],2],EvenQ[Total[#]]&],If[First@Normal[latticeDataset[Select[#CompoundtoCompound[list]&],"Structure"]]=="face-centered cubic",Select[Flatten[Table[{h,k,l},{h,0,n},{k,0,n},{l,0,n}],2],Length@DeleteDuplicates[EvenQ/@#]1&],{}],{}]),{}],{}],1]

Here is an example:

In[]:=

reflections[{"Na"},2]

Out[]=

{{0,0,2},{0,1,1},{0,2,0},{0,2,2},{1,0,1},{1,1,0},{1,1,2},{1,2,1},{2,0,0},{2,0,2},{2,1,1},{2,2,0},{2,2,2}}

Now, we proceed to group Miller indices by d spacing (“a”, the lattice constant, is left out since it is consistent across all planes).

In[]:=

grouped[list_,n_]:=GroupBy[reflections[list,n],1/Sqrt[(#[[1]]^2+#[[2]]^2+#[[3]]^2)]&]

Here is an example:

In[]:=

grouped[{"Li1+","Cl1-"},2]

Out[]=



{{0,0,2},{0,2,0},{2,0,0}},

{{0,2,2},{2,0,2},{2,2,0}},

{{1,1,1}},

{{2,2,2}}

The keys of this function are transformed from the normalized d-spacing to theta values. For unary systems, I used the Wolfram database to import the lattice constant to obtain accurate d-spacing. For binary systems, a handmade dataset was used to extract lattice constants.

In[]:=

keytransform[w_,list_,n_]:=If[Length@list1,theta[QuantityMagnitude[UnitConvert[First@ElementData[ElementData[First@list,"StandardName"],"LatticeConstants"],"Angstroms"]]*(grouped[list,n]//Keys),w]//N,If[Length@list2,theta[First[Normal[latticeDataset[Select[#CompoundtoCompound[list]&],"LatticeConstant"]]]*(grouped[list,n]//Keys),w]//N,{}],{}]

A list of associations is made so theta values and Miller indices can be called easily.

In[]:=

association[list_,n_,w_]:=Sort[MapThread[#1#2&,{keytransform[w,list,n],grouped[list,n]//Values}]]

Here is an example:

In[]:=

association[{"Na1+","Cl1-"},3,1.54]

Out[]=

{0.477458{{1,1,1}},0.553123{{0,0,2},{0,2,0},{2,0,0}},0.79291{{0,2,2},{2,0,2},{2,2,0}},0.93981{{1,1,3},{1,3,1},{3,1,1}},0.98524{{2,2,2}},1.27477{{1,3,3},{3,1,3},{3,3,1}},1.5773{{3,3,3}}}

Atomic Form Factors

Importing another database for values to be used for calculating the atomic form factor.

In[]:=

Import["C:\\Users\\hamza\\Desktop\\project\\Untitled spreadsheet.xlsx","Elements"]

Out[]=

{Data,Dataset,Dimensions,FormattedData,Formulas,Images,SheetCount,Sheets}

In[]:=

atomic=Import["C:\\Users\\hamza\\Desktop\\project\\Untitled spreadsheet.xlsx","Dataset"]

Out[]=



Element	a1	b1	a2	b2	a3	b3	a4	b4	c
H	0.489918	20.6593	0.262003	7.74039	0.196767	49.5519	0.049879	2.20159	0.001305
H1-	0.897661	53.1368	0.565616	15.187	0.415815	186.576	0.116973	3.56709	0.002389
He	0.8734	9.1037	0.6309	3.3568	0.3112	22.9276	0.178	0.9821	0.0064
Li	1.1282	3.9546	0.7508	1.0524	0.6175	85.3905	0.4653	168.261	0.0377
Li1+	0.6968	4.6237	0.7888	1.9557	0.3414	0.6316	0.1563	10.0953	0.0167
Be	1.5919	43.6427	1.1278	1.8623	0.5391	103.483	0.7029	0.542	0.0385
Be2+	6.2603	0.0027	0.8849	0.8313	0.7993	2.2758	0.1647	5.1146	-6.1092
B	2.0545	23.2185	1.3326	1.021	1.0979	60.3498	0.7068	0.1403	-0.1932
C	2.31	20.8439	1.02	10.2075	1.5886	0.5687	0.865	51.6512	0.2156
Cval	2.26069	22.6907	1.56165	0.656665	1.05075	9.75618	0.839259	55.5949	0.286977
N	12.2126	0.0057	3.1322	9.8933	2.0125	28.9975	1.1663	0.5826	-11.529
O	3.0485	13.2771	2.2868	5.7011	1.5463	0.3239	0.867	32.9089	0.2508
O1-	4.1916	12.8573	1.63969	4.17236	1.52673	47.0179	-20.307	-0.01404	21.9412
F	3.5392	10.2825	2.6412	4.2944	1.517	0.2615	1.0243	26.1476	0.2776
F1-	3.6322	5.27756	3.51057	14.7353	1.26064	0.442258	0.940706	47.3437	0.653396
Ne	3.9553	8.4042	3.1125	3.4262	1.4546	0.2306	1.1251	21.7184	0.3515
Na	4.7626	3.285	3.1736	8.8422	1.2674	0.3136	1.1128	129.424	0.676
Na1+	3.2565	2.6671	3.9362	6.1153	1.3998	0.2001	1.0032	14.039	0.404
Mg	5.4204	2.8275	2.1735	79.2611	1.2269	0.3808	2.3073	7.1937	0.8584
showing 1–20 of 213



Getting the Columns

In[]:=

dataset=atomic[[1]];

In[]:=

columns=Normal[dataset]//First

Out[]=

{Element,a1,b1,a2,b2,a3,b3,a4,b4,c}

In[]:=

data=Rest[Normal[dataset]];

Making a wolfram dataset

In[]:=

assocData=Association@@MapThread[Rule,{columns,#}]&/@data;

In[]:=

newDataset=Dataset[assocData];

In[]:=

newDataset

Out[]=

Element	a1	b1	a2	b2	a3	b3	a4	b4	c
H	0.489918	20.6593	0.262003	7.74039	0.196767	49.5519	0.049879	2.20159	0.001305
H1-	0.897661	53.1368	0.565616	15.187	0.415815	186.576	0.116973	3.56709	0.002389
He	0.8734	9.1037	0.6309	3.3568	0.3112	22.9276	0.178	0.9821	0.0064
Li	1.1282	3.9546	0.7508	1.0524	0.6175	85.3905	0.4653	168.261	0.0377
Li1+	0.6968	4.6237	0.7888	1.9557	0.3414	0.6316	0.1563	10.0953	0.0167
Be	1.5919	43.6427	1.1278	1.8623	0.5391	103.483	0.7029	0.542	0.0385
Be2+	6.2603	0.0027	0.8849	0.8313	0.7993	2.2758	0.1647	5.1146	-6.1092
B	2.0545	23.2185	1.3326	1.021	1.0979	60.3498	0.7068	0.1403	-0.1932
C	2.31	20.8439	1.02	10.2075	1.5886	0.5687	0.865	51.6512	0.2156
Cval	2.26069	22.6907	1.56165	0.656665	1.05075	9.75618	0.839259	55.5949	0.286977
N	12.2126	0.0057	3.1322	9.8933	2.0125	28.9975	1.1663	0.5826	-11.529
O	3.0485	13.2771	2.2868	5.7011	1.5463	0.3239	0.867	32.9089	0.2508
O1-	4.1916	12.8573	1.63969	4.17236	1.52673	47.0179	-20.307	-0.01404	21.9412
F	3.5392	10.2825	2.6412	4.2944	1.517	0.2615	1.0243	26.1476	0.2776
F1-	3.6322	5.27756	3.51057	14.7353	1.26064	0.442258	0.940706	47.3437	0.653396
Ne	3.9553	8.4042	3.1125	3.4262	1.4546	0.2306	1.1251	21.7184	0.3515
Na	4.7626	3.285	3.1736	8.8422	1.2674	0.3136	1.1128	129.424	0.676
Na1+	3.2565	2.6671	3.9362	6.1153	1.3998	0.2001	1.0032	14.039	0.404
Mg	5.4204	2.8275	2.1735	79.2611	1.2269	0.3808	2.3073	7.1937	0.8584
Mg2+	3.4988	2.1676	3.8378	4.7542	1.3284	0.185	0.8497	10.1411	0.4853
showing 1–20 of 212

F is the function that approximates the form factors as a sum of gaussians. See https://en.wikipedia.org/wiki/Atomic_form_factor

F[{a_,b_,c_,w_,theta_}]:=(a*Exp[-b(Sin[theta/2]/w)^2]+c)

Making a function to extract data. Takes the a_i and b_i values as well as c and plugs it into F to get the atomic form factors.

In[]:=

atomdata[e_,theta_,w_]:=Total[F/@Table[{First[Normal[newDataset[Select[#Elemente[[1]]&]]]][[i]],First[Normal[newDataset[Select[#Elemente[[1]]&]]]][[i+1]],First[Normal[newDataset[Select[#Elemente[[1]]&]]]][[10]],w,theta},{i,2,8,2}]]sc[in_,w_]:=Plot[atomdata[in,theta,w],{theta,0,Pi/2},AxesLabel{"Angle","Atomic Form Factor"}]

“sc” plots the atomic form factor as a function of the angle

In[]:=

sc[{"C"},1.54]

Out[]=

Here is an example of the atomdata function:

In[]:=

atomdata[#,.8,1.54]&/@{{"Li1+"},{"C"}}

Out[]=

{1.69118,3.56636}

Structure Factor Calculation

For binary FCC systems, the parity of the Miller indices has to be accounted for. If the Miller indices are even, then a total of the atomic form factors is used for the structure factor. If the indices are odd, the difference is taken.

In[]:=

evenodd[b_,elementlist_,theta_,w_]:=If[b,Total[atomdata[#,theta,w]&/@elementlist],Differences[atomdata[#,theta,w]&/@elementlist]//First]

The structure factor is different for each type of structure. It is given by this formula:

Where f_j denotes the jth atomic form factor and (x,y,z) indicate atom position. For BCC and FCC, this formula simplifies greatly. Evenodd was used for binary systems to account for the parity of the Miller indices.

structurefactor[elementlist_,w_,list_]:=If[Length@elementlist1,If[ElementData[First@First@elementlist,"CrystalStructure"]["Name"]"body-centered cubic",2*atomdata[Flatten@elementlist,#,w]&/@(list//Keys),If[ElementData[First@First@elementlist,"CrystalStructure"]["Name"]=="face-centered cubic",4*atomdata[Flatten@elementlist,#,w]&/@(list//Keys),{}],{}],If[Length@elementlist2,4*MapThread[evenodd[#1,elementlist,#2,w]&,{(EvenQ/@First/@First/@(list//Values)),list//Keys}],{}],{}]

Multiplicity

Take a look at the following graphic of planes given by Miller indices:

File:Miller Indices Felix Kling.svg. (n.d.). Retrieved from https://commons.wikimedia.org/wiki/File:Miller_Indices_Felix_Kling.svg

You might notice that if we reflect (100) we can get (010) and (001) . We can also get negative indices, usually denoted

instead of -1. This gives us 6 total planes that are symmetry-equivalent, and correspond to the same peak. Hence, we say that the class of Miller indices (h00) has a multiplicity of 6. These multiplicities range from 6 to 48 for a cubic lattice structure, but can get as low as 2 with less symmetric structures.

Therefore, instead of calculating the contributed intensity of each plane, we count them as one plane and multiply the resultant intensity by a specific multiplicity. This multiplicity is then used to calculate peak intensity.

In[]:=

multiplicity[list_]:= Which[ MemberQ[{list},{h_,h_,h_}],8, MemberQ[{list},{h_,0,0}],6, MemberQ[{list},{0,k_,0}],6, MemberQ[{list},{0,0,l_}],6, MemberQ[{list},{h_,h_,0_}],12, MemberQ[{list},{0_,k_,k_}],12, MemberQ[{list},{h_,k_,0}],24, MemberQ[{list},{h_,0,l_}],24, MemberQ[{list},{0,k_,l_}],24, MemberQ[{list},{h_,h_,l_}],24, MemberQ[{list},{h_,k_,l_}],48]

Here is an example:

In[]:=

multiplicity[{1,1,1}]

Out[]=

Intensity Calculation

This intensity function gives the intensity for each peak, and does so by multiplying three factors: Lorentz Polarization correction, multiplicity, and the square of the structure factor.

In[]:=

intensity[w_,elementlist_,n_]:=Transpose@{(association[Flatten@elementlist,n,w]//Keys),(.5(1+(Cos[#])^2)/(Sin[#/2]^2*Cos[#/2]))&/@(association[Flatten@elementlist,n,w]//Keys)*(multiplicity/@(Last/@(association[Flatten@elementlist,n,w]//Values)))*(structurefactor[elementlist,w,(association[Flatten@elementlist,n,w])])^2}

Here is an example:

In[]:=

intensity[1.54,{{"Cu"}},2]

Out[]=

{{0.755735,509100.},{0.880166,242598.},{1.2932,147611.},{1.65984,55657.5}}

Getting the Final Plot

“peak” takes a set of theta values and their respective intensities, which are given by the “intensity” function. An arbitrary peak shape was chosen, and the -10000 is an arbitrary constant. If Rietveld refinement were to be used, this constant would be optimized and peak shape would change as well.

In[]:=

peak[{theta_,intensity_}]:=intensity*Exp[-10000Pi(t-theta)^2]

In[]:=

p=peak[#]&/@intensity[1.54,{{"Ag"}},2]

Out[]=

2.88657×

-10000π

(-0.665108+t)



,1.4363×

-10000π

(-0.773027+t)



,986121.

-10000π

(-1.12453+t)



,362362.

-10000π

(-1.42286+t)





In[]:=

Quiet[Plot[Total[p]/.t(x/90*Pi/2),{x,30,80},PlotRangeAll,AxesLabel{"2 theta","Intensity"}]]

Out[]=

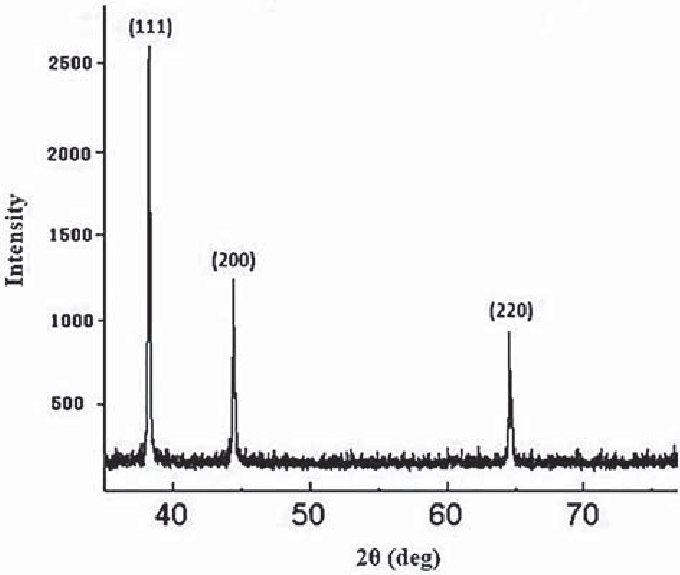
Summary

In this project, simple mathematical models of XRD were used to predict various XRD patterns, for both unary and binary systems. For unary systems, the peaks and relative intensities were predicted with high accuracy. However, binary systems showed mediocre results, as relative intensities were often wrong. Attempts at effective prediction of lattice structure from first principles failed. Multiplicities were manually entered instead of being computed, however, crystallographic point groups showed significant promise in computing multiplicities. The crystallographic point group approach was not feasible given the two week time constraint.

Future Work

Thanks to Mr. Wolfram, I certainly have a lot to do this summer! The eventual goal of this project is to create software with a simple UI, ie the user has to type in as little data as possible, that can predict the XRD pattern of complex inorganic lattice structures. This software would be used by scientists and industry experts alike to have reference patterns for experimental results. The first step in realizing this goal is improving accuracy for binary systems, and expanding from only cubic structures to more complex structures such as hexagonal and monoclinic lattice structures. More complicated multiatomic structures will then be implemented as well.

Perhaps the most ambitious of my future plans is doing the inverse problem: predicting the lattice structure from a given XRD pattern using machine learning. Ideally, a machine learning algorithm would be trained on a large dataset generated by the expanded XRD prediction software, and eventually be tested on the Inorganic Crystal Structure Database (ICSD).

Acknowledgements

I would like to thank my mentor, Eryn Gillam, for helping me throughout my project. I would also like to thank the other mentors for their help, and Mohammad Bahrami for his lectures. Wolfram Summer Camp truly gave me an outlet to express my creativity in novel ways, and the two weeks I spent here were invaluable. Wolfram Summer Camp gave me a novel perspective on how to approach all aspects of life, and key insight into how computational thinking can change the world. For these reasons and more, I am beyond grateful to have been a part of this camp, and am looking forward to apply my new skills.

References

- Miller indices pictures. Miller Indices Felix Kling.svg. (n.d.). Retrieved from WikiMedia

- Predicted vs Experimental Silver XRD Pattern. Experimental plot obtained from: Koohpeima, Fatemeh & Mokhtari, Mohammad & Samaneh, KHALAFI. (2017). The effect of silver nanoparticles on composite shear bond strength to dentin with different adhesion protocols. Journal of Applied Oral Science. 25. 367-373. 10.1590/1678-7757-2016-0391.

Cite this as: Hamza Alsamraee, "A Computational Method to Predict X-ray Diffraction (XRD) Patterns" from the Notebook Archive (2019), https://notebookarchive.org/2019-08-0gjful4