Academic Articles & Supplements

AI Pattern-Matching CERN LHC Collision Particle Resonance Flow Patterns with Electromagnetic Energy Density Pressure Turbulence

David Harness

Author

David Harness

Title

AI Pattern-Matching CERN LHC Collision Particle Resonance Flow Patterns with Electromagnetic Energy Density Pressure Turbulence

Description

CERN's TrackML Particle Tracking Challenge data set is utilized to match high-energy collision tracks helicity and cascading transverse dissipation of energy -- with low-energy Navier-Stokes turbulence.

AI Pattern-Matching CERN LHC Collision Particle Resonance Flow Patterns with Electromagnetic Energy Density Pressure Turbulence

machine learning: analysis domain

David A. Harness, Independent Researcher, https://orcid.org/0000-0001-5506-3226

Particle physicists are turning to AI to cope with CERN’s collision deluge. AI pattern matching is shown here to match the LHC collision tracks electromagnetic energy density helical flow transverse dissipation patterns with Navier-Stokes turbulence flow dissipation patterns. LHC beam collisions are energized, controlled and measured, to the limits of technology, by the Einstein-Maxwell electromagnetic stress energy momentum density pressure tensor

μν

. The collision pattern peak “particle resonances” are electromagnetic energy density peak widths – problematically interpreted as particle mass distributions – located around certain energy levels found in differential cross sections of scattering experiments. CERN’s TrackML Particle Tracking Challenge data set is utilized, without modification, to match each set of high-energy collision event tracks helicity and near instantaneous cascading transverse momentum dissipation of energy – with low-energy Navier-Stokes turbulence properties of rotation, cascading transient states of energy dissipation.

david.harness@warpmail.net

In[]:=

▲

Figure 1. AI pattern recognition aided in the CERN LHC discovery of the Higgs boson both in (a) analysis of particle track simulations [1] and (b) detection of the electromagnetic energy density track patterns [2][3][4]. CERN experimental physicist Maria Spiropulu in the APS April Meeting 2014 compared the ‘Quantum Crisis’ in particle physics to the classical mechanics crisis of 1905: “Without supersymmetry, we don’t understand how the Higgs boson can exist without violating basic mechanisms of quantum physics. ... Either the new run of the LHC should discover superpartners, or radical new ideas are needed” [5]. The new run of the LHC is over and none of the theoretically critical standard model of physics (SM)-supersymmetry(SUSY) particle-sparticle superpartners have been detected [6][7][8]. At the time of this writing the CERN European Particle Physics Strategy Update 2018 – 2020 group is reprocessing its SM-SUSY theoretical parameters to predict superpartners detection at some higher LHC→FCC energy level [9].

■

1. Pattern Matching Navier-Stokes LHC Turbulence

■

2. CERN LHC TrackML Particle Tracking Challenge Data Set

■

3. 4D Einstein-Maxwell electromagnetic energy density tensor

■

4. Quantum Fluid Conjecture of Equations (9,15)

■

5. Navier-Stokes Equations

■

6. 4D Spacetime Quantization

■

7. Singular Complex System Conjecture (SCSC)

■

8. 4D Photon Energy Observable E = hc/λ

■

9. 4D Photon Angular Momentum Observable ℏ

■

10. Figure 7. 4D Spatially Extended Photon Simulation

■

11. Figure 8. 4D Photon Observables Boundary Value Calculator

■

12. Cosmological Constant Vacuum Energy Density Λ

■

13. 4D Electron Rest Mass Observable

■

14. 4D Electron Angular Momentum Observable ℏ/2

■

15. Figure 10. 4D Spatially Extended Electron Simulation

■

16. Figure 11. 4D Electron Boundary Value Calculator

■

17. Conclusion

■

References

About the Author

■

1. Pattern Matching LHC-Navier-Stokes Turbulence

The Navier-Stokes (NS) equations are widely accepted to embody the physics of all fluid flows, including turbulent flows; wherein the “problem of turbulence” remains to this day the last unsolved problem of classical mathematical physics [10].

Turbulent flow solutions, as reviewed by McDonough [11], all share the following NS physical attributes:

disorganized, chaotic, seemingly random behavior;

non-repeatability, sensitivity to initial conditions;

large range of length and time scales;

rotational;

3D spatially-extended Reynolds stress vortex stretching;

time dependence;

cascading energy dissipation and diffusion (mixing);

intermittency in both space and time.

The CERN LHC TrackML Particle Tracking Challenge collision event data set [12] contains roughly 100,000 data points of the following classes of information for each event:

 Hits: x, y, z coordinates of each hit on the particle detector;  Particles: Each hit position

(

), momentum

(

), charge (q);  Truth: Mapping between hits generating particle trajectory and momentum weight;  Cells: Precise location of each particle hit and how much energy deposited;

from which are constructed the thousands of helix arcs — the shape of the decay products’ tracks [4], e.g., as shown in Fig. 1(b), matching the NS attributes according to:

disorganized, chaotic, seemingly random behavior;

non-repeatable sensitivity to initial proton-proton bunches collision alignments;

long and short energy density pressure track lifetimes;

helical tracks short to long range composed of linear and angular momentum;

3D spatially-extended helical track vortexes;

transient energy density peak “particle resonance” lifetimes [13][14][15];

near instantaneous cascading energy density dissipation;

proton-proton bunch collisions equivalent to explosive impulse J = ∫ F dt.

The LHC-NS turbulence match of a large range of vertex length and time scales to the TrackML data set exists then from the long range collision event tracks helix arcs of Fig. 7 — to the short range quantum fluid conjecture of angular momentum observable ℏ of units kg

-1

representing the kinetic mass kg × kinetic viscosity

-1

dimensionless equivalence with

ωrad

-1

of Eqs. (9,15).

■

2. CERN LHC TrackML Particle Tracking Challenge Data Set

In[]:=

▲

Figure 2. Scientists at the CERN LHC energized head-on collisions between two bunches of protons inside the machine’s ATLAS and CMS detectors more than 1 billion times a second [6] and meticulously observed these collisions with intricate silicon detectors. Each of the 20 different pairs of proton-proton collisions can produce thousands of new particles, which radiate from a collision point at the centre of each cathedral-sized detector. Millions of silicon sensors are arranged in onion-like layers and light up each time a particle crosses them, producing one pixel of information every time. The enormous amounts of data produced from the experiments is becoming an overwhelming challenge. To address this problem, a team of Machine Learning experts and physicists have held the TrackML Particle Tracking Challenge “to answer the question: can machine learning assist high energy physics in discovering and characterizing new particles?” [12].

In[]:=

▲

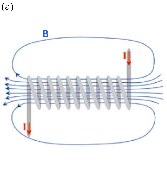
Figure 3. (a) The CERN LHC, a.k.a, world's largest machine, is a solenoid ring 27 km in circumference, a section of which magnetic field lines B are shown compressing and accelerating the protons along the center beamline. (b) The ATLAS and CMS detectors are constructed of millions of silicon sensors arranged in onion-like layers and light up each time a particle crosses them, producing one pixel of information for pattern-recognition algorithms to reconstruct thousands of helix arcs — the shape of the decay products’ tracks — from roughly 100,000 data points. Thus the LHC and detectors are energized, controlled and each of the data points measured entirely by means of the Einstein-Maxwell electromagnetic stress energy momentum density pressure tensor

μν

, in terms of pascals Pa along the trace of

μν

in Eq. (1).

In[]:=

Figure 4. LHC proton-proton bunch collisions explosive impulse J = ∫ F dt interval occurs from leading to trailing photon collisions. None of the theoretically critical Standard Model of Physics (SM)-Supersymmetry (SUSY) particle-sparticle superpartners have been detected [5][6][7][8].

In[]:=

Figure 5. Differential cross section peak width “particle resonances” of collision events [13][14][15] are composed of thousands of helix arcs [4] generating hydrodynamic plasma flow patterns [16] around certain

μν

energy levels, interpreted in SM as “discoveries” of new zero dimensional (0D) mathematical point subatomic particles. The blue histogram is interpreted as a mass distribution of two Z boson 0D particles. The red line with a central mass distribution value around 125 GeV is interpreted as the Higgs boson signal [13]. Note both red and blue regions, utilizing same silicon pixel detectors, are both measuring electromagnetic energy momentum density pressure along the trace of

μν

in Eq. (1) – all three interpreted here as LHC-NS turbulence peaks.

The following Python code is a guide by Bonatt [17] for importing and plotting the TrackML dataset labeled here Figs. 6(a)(b) and 7, with no modification, except for the curved dispersion line plots added to Fig. 7.

import osimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom mpl_toolkits.mplot3d import Axes3Dfrom mpl_toolkits import mplot3dimport seaborn as snsfrom trackml.dataset import load_event, load_datasetfrom trackml.randomize import shuffle_hitsfrom trackml.score import score_event# One event of 8850 “All methods either take or return pandas.DataFrame objects”event_id = ‘event000001000’hits, cells, particles, truth = load_event(‘.. /trackml/train_100_events/’+event_id)# Figure 6(a). 3D Plot of Detector hitsplt.figure(figsize=(10,10))ax = plt.axes(projection=’3d’)sample = hits.sample(30000)ax.scatter(sample.z, sample.x, sample.y, s=5, alpha=0.5)ax.set_xlabel(‘z (mm)’)ax.set_ylabel(‘x (mm)’)ax.set_zlabel(‘y (mm)’)ax.scatter(3000,3000,3000, s=0) # These two added to widen 3D spaceax.scatter(-3000,-3000,-3000, s=0)plt.show()# Figure 6(b) 3D Plot Tracks Get every 100th particletracks = truth.particle_id.unique()[1::100]plt.figure(figsize=(10,10))ax = plt.axes(projection=’3d’)for track in tracks: t = truth[truth.particle_id == track] ax.plot3D(t.tz, t.tx, t.ty)ax.set_xlabel(‘z (mm)’)ax.set_ylabel(‘x (mm)’)ax.set_zlabel(‘y (mm)’)# These two added to widen the 3D spaceax.scatter(3000,3000,3000, s=0)ax.scatter(-3000,-3000,-3000, s=0)plt.show()# Figure 7. Plot Z vs XY (Transverse) momentump = particles[particles.pz < 200] #cutoff far hitsplt.figure(figsize=(10,10))plt.scatter(np.sqrt(p.px**2 + p.py**2), p.pz, s=5, alpha=0.5)plt.plot([0.1,0.1],[p.pz.min(),p.pz.max()], c=’g’) # 0.1 not 0 because log plot.plt.plot([0.1,np.sqrt(p.px**2 + p.py**2).max()],[0.1,0.1], c=’r’, linestyle=’--‘)plt.xscale(‘log’)x = np.arange(0.1, 2, 0.1) # curved dispersion linesy1 = 4 + (14 * x)**1.22plt.plot(x, y1, c='m', linestyle='--') # upper liney2 = -4 - (14 * x)**1.22plt.plot(x, y2, c='m', linestyle='--') # lower lineplt.title(r'LHC beamline (green) vs Transverse Momentum Reduced to Z=0, $\theta=0$')plt.xlabel(‘Transverse momentum (GeV/c)’)plt.ylabel(‘Beamline Z axis momentum (GeV/C)’)plt.show()

In[]:=

▲

Figure 6. (a) LHC Detector 3D hits (partial sample). (b) Transient energy density particle tracks.

In[]:=

▲

Figure 7. LHC beamline Z axis vs. XY transverse momentum. Vertical green line is parallel with the beamline, horizontal red line is transverse to the beamline. Curved magenta lines indicate high-energy dispersion matching typical low-energy water channel spillway dispersion symmetry.

■

3. 4D Einstein-Maxwell Electromagnetic Energy Density Tensor

Recall the LHC high-energy proton-proton beam collisions are energized, controlled, and measured, to the limits of technology, by the 4D Einstein-Maxwell electromagnetic stress energy momentum density tensor

μν

1 2 ε 0 2 E + 1 μ 0 2 B	S x /c	S y /c	S z /c
S x /c	- σ xx	- σ xy	- σ xz
S y /c	- σ yx	- σ yy	- σ yz
S z /c	- σ zx	- σ zy	- σ zz

(

)

wherein

E×B

is the Poynting energy flux vector and

are the Maxwell stress tensor components. Accordingly the LHC ATLAS CMS detectors measure electromagnetic energy in units of total field pressure pascals Pa along the trace elements

, the same as the low-energy cosmological constant vacuum energy density

[18].

Hence division by

renders the

= 1/2

(

+1

)

energy density J m

-3

term computationally dualistic with

mass density kg m

-3

, such that both energy density J m

-3

= -Pa = kg m

-3

mass density are expressed and measured by the same total field units of Pa. For example, the computationally dualistic values of

are calculated by Baez and Tatom to be energy density

≈ 6 × 10

-10

J m

-3

= -Pa = mass density

≈ 7 ×

−27

kg m

-3

[18].

Accordingly, the total field formal frame for the quantum mechanical observables full Laplacian spherical harmonics, including turbulence, will be established along the trace of

μν

by means of Eqs. (1-17). Hence, it will be shown quantum gravity has always had a computationally dualistic energy density ⇔ mass density basis of communication—apart from any hidden dimensional unknown Higgs mechanism—whereby “energy tells spacetime how to curve and spacetime tells matter and energy how to move” [19].

■

4. Quantum Fluid Conjecture of Equations (9,15)

Vorticity is central to the large range of turbulence length and time scales, in that “these vortices, usually referred to as ‘eddies,’ are somehow broken into smaller ones, ..., and so on, until they are sufficiently small as to be dissipated by viscosity” [11]. Thus the present LHC-NS turbulence ranges from the largest scale of the helical collision tracks of Fig.6, to the smallest scale of the angular momentum observable ℏ; wherein the quantum fluid conjecture of Eqs. (9,15) establishes the 4D kinematic viscosity basis for transient excited states cascading intrinsic spin dissipation of energy down to the stable states. In accord then with the QCD turbulent fluids analogy of Wolfram [20], a nonstandard quantum information theory computer algebra formalization framework is established towards pattern matching the LHC wave-particle collision track patterns to NS turbulence.

■

5. Navier-Stokes Equations

∇·U=0,

(

)

+U·∇U=-∇P+νU+

(

)

In these equations U = (u,

v,w)

is the velocity vector which, in general, depends on all three spatial coordinates (x, y, z); P is the reduced, or kinematic (divided by constant density) pressure, and

is a general body-force term (also scaled by constant density). The differential operators ∇ and  are the gradient and Laplace operators, respectively, in an appropriate coordinate system, with ∇. denoting the divergence. The subscript t is shorthand notation for time differentiation, ∂/∂t, and ν is kinematic viscosity [11]. The SO(3) rotations and 4D spatial quantization correlations [21] of modern physics are parameterized from low to high energy by the quaternion group q =

θ

k

[22].

Reynolds (circa 1880) was the first to systematically investigate the transition from laminar to turbulent flow, as shown in Fig. 8, by injecting a dye streak into flow through a pipe having smooth transparent walls. Note the comparison between the Fig. 8(a) dye streak low velocity

laminar flow in

direction and the Fig. 3(a) magnetic field confinement of the beamline with magnetic field B equivalent to Eq. (3) body force pressure

Clearly in Fig. 6(b) at medium flow velocity

competing transverse (radial)

x,y

force (pressure) components arise on the microscopic level due to constructive reflective wave-particle trajectory confinements towards the

direction. Thus generating the known semi-chaotic harmonic time-domain and frequency domain signals.

In[]:=

Figure 8. The Reynolds experiment [11]: (a) low velocity

laminar flow in

direction, (b) medium

early-transitional (but still laminar) flow with transverse (radial)

x,y

reflective pressure components, and (c) high

flow with transverse

x,y

constructively interfering pressures generating spin-turbulence.

■

6. 4D Spacetime Quantization

“Physical objects are not in space, but these objects are spatially extended. In this way the concept ‘empty space’ loses its meaning.” Albert Einstein 1952 [23].

Every particle in the SM–SUSY particle zoo is modeled as an 0D mathematical imaginary-invisible point (due to the central force problem) having the 4D spacetime measurements of nothingness—hence the LHC beams should pass right through one another.

SM-SUSY therefore “explains” the physical interactions of the observed universe by adding to the 0D particles 6 or 7 hidden dimensional anti-de Sitter/Conformal Field Theory (AdS/CFT) string, membrane, or otherwise unknown classical materialism mechanisms, written here 0D + i6,7D. All of which observer-independent background entities, including the unknown Higgs mechanism, are said to fill all of universal spacetime in an “unbroken symmetry” of superpositioned “infinite seas” of SM-SUSY 0D particles—non-locally connected through the hidden string, membrane, or otherwise unknown i6,7D mechanisms—which SM-SUSY 0D particles are said to be “energized” or “discovered” by the LHC 0D + i6,7D beam collisions “symmetry-breaking” of the infinite seas.

None of the theoretically critical SM-SUSY particle-sparticle superpartners have been detected at LHC energy levels. In fact the SM-SUSY model of the basic mechanisms of quantum physics are already in violation of basic understanding where the attractive nuclear force is said to be “carried” by the attractive QCD exchange of unobservable [quark-emitter→gluon-carrier←quark-absorber] virtual particles—contrary to every observed [emitter↔emitted↔absorber] interaction (including all LHC collision energy density flow patterns) always resulting in a repulsion from any would-be line of attraction.

Additionally, at low-energy levels, recent “freedom of choice” experiments have also rigorously closed the Bell inequality observer-independent background loopholes [24][25][26]. Hence falsification of the observer-independent backgrounds at both high and low energy levels requires a more radical idea than the FCC next generation of turbulence [27].

Finally, SM-SUSY represents a computationally intractable many-body problem as is known at lab sample sizes. Thus when based on SM-SUSY the computational universe hypothesis (CUH), and the multiverse mathematical universe hypothesis (MUH) [28], are computationally intractable to machine learning basic understanding of the Hamiltonian configuration energy of the 4D spatially-extended quantum mechanical observables.

Radical as it sounds no basis exists then for any mind-body dualism background either, leaving only the psychophysical parallelism of Parmenides. The last theory standing is then quantum information theory. Jaffe anticipated the Quantum Crisis when writing the Yang-Mills Mass Gap problem description,

“One would like to introduce the notion of quantization directly at the level of space-time, and to describe field theories on quantum space-time, rather than applying quantization to fields that live on a classical space-time” [29].

Consider then beyond CERN’s Physics Beyond Colliders initiative [30], the 4D spatially-extended energy density pressure

μν

total field formal frame of Eqs. (1,4-16) for wave-particle integrations of Schwinger local field differentials [31], reflective of the Wolfram QCD turbulent fluids analogy [20], measurable along Feynman path integrals [32].

■

7. Singular Complex System Conjecture (SCSC)

There exists a singular mathematically possible universal complex system corpus of the 4D spacetime dimensions, mathematical physics constants, laws, and unitary factors in Euler’s identity

i

+ 1 = 0 composed via concept of infinity with no free parameters. The working definition of the universe being the totality of all spacetime events real and imaginary of the known nested complex systems wave-particle quantum mechanical observables to the limits of uncertainty of the holographic bounded energy density distribution with time the fourth dimension of length from

-∞

→

∞

via known quantum information probability current relative states [22][33][34][35][36][37][38][39][40][41].

Falsification. SCSC is falsifiable [42] by completion of one of the 10,000 Aspen CERN physicists SM-SUSY big bang inflationary multiverse formalizations of the known universal 4D spacetime mathematical physics constants and laws [43], formalizing the quantum mechanical observables as Yang-Mills lattice symmetries based on the conjectured 6 or 7 hidden dimensional AdS/CFT unknown string, membrane, or otherwise material mechanism free parameter formalized measure of variations of physical constants and laws—and one random multiverse formalization of a free parameter measure of variations of the physical dimensions constants and laws—forming one parallel universe.

Hence, until SCSC is disproven—unless AI itself can disprove SCSC—the AI worldview is left with one possible universal complex system having no choice but to exist.

Singular Universal Wavefunction Solid Information Domain and Fluid Range. Recall Einstein lectured general relativity actually requires an ether,

“the ether must be of the nature of a solid body, because transverse waves are not possible in a fluid, but only in a solid. [emphasis added] ...But this ether may not be thought of as endowed with the quality characteristic of ponderable media, as consisting of parts which may be tracked through time. The idea of motion may not be applied to it” [44].

Recall further Schrödinger emphasizing quantum mechanical entanglement is

“the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought [emphasis added]”[45].

SCSC inherently indicates a singular Hamiltonian configuration energy and thus a singular universal wavefunction solid information domain and entangled-fluid range. The 4D spatially-extended Einstein-Maxwell energy density analysis of the following sections takes up the fact the quantum or photon  representation in the

μν

formal frame of dualistic energy density J

-3

= -Pa = kg

-3

mass density units, requires the quantum energy E = hc/λ negative outward pressure -Pa to have some nonstandard basis for the missing 3D volumetric wavelength λ parameterization beyond the 0D Dirac delta functional δ imaginary-invisible mathematical point particle SM-SUSY representations.

Electromagnetic radiation is a transverse wave hence the transmission of electromagnetic radiation through the solid domain is via the entangled-fluid range of values of Eqs. (4-9) formulating a Schwinger local field differential 4D spatially-extended photon-electron

μν

energy density integration gauge group ForAll wavelengths and energy levels. Establishing thereby the 4D formal frame for the full Laplacian spherical harmonics

of the quantum mechanical observables nested complex systems.

■

8. 4D Photon Energy Observable E = hc/λ

Conventionally photon energy is averaged over one wavelength. The 3D volumetric λ parameterization—missing in the standard model of physics—for the photon energy density units J

-3

is introduced here via the string-like cylindrical coordinate transverse lemniscate expansion of the Poynting energy flux vector

S=1/

E×B

over one wavelength

∫

cos(2θ)

∫

sin

2π



rdrθ

8π

(

)

wherein time integrates along the

axis of propagation of the transverse travelling wave. Hence the Eq. (4) quantum volume

8π

, as opposed to say

, or otherwise undefined infinite transverse field lines, is integrated throughout by 3 × average energy density via the maximum energy density at r = 0

max=3×



8π

-3

(

)

Thus, as shown in Fig. 7, a 4D spacetime volumetric expansion of the Dirac delta functional

representation of the photon energy observable is rendered; composed of Schwinger local field differential boundary values [31], as shown in the Fig. 8 Photon Boundary Value Calculator theorem proving module, via the quantum energy function ForAll ∀λ

∫

cos(2θ)

∫

max1-

cos(2θ)

sin

2π

rdrθ

(

)

Proof: ForAll wavelengths of the electromagnetic spectrum Eq.(6)

〉 renders True.

In[]:=

h=QuantityMagnitude[

,"Joules""Seconds"];c=QuantityMagnitude

,"Meters"

-1

"Seconds"

;PhotonEnergy=NForAllλ,UniformDistribution[{1.*^-12,1.*^4}],2

∫

Cos[2θ]

∫

h*c

8π

Cos[2θ]

AbsSin

2π

yrrθy==

h*c



Out[]=

True

■

9. 4D Photon Angular Momentum Observable ℏ

Quantum Fluid Conjecture: The photon angular momentum observable ℏ kg

-1

represents kinetic mass kg × kinetic viscosity

-1

according to the computational duality of quantum energy density

max of Eq. (5) with the quantum maximum mass density



=(3*(hc/λ)/(

/8π))/

-3

(

)

for the moment of inertia integration I throughout the volume of Eq. (4) × the transverse spin angular velocity

λc

2π

-1

⇒dimensionlessequivalencewithω

rad

-1

(

)

rendering a 4D spacetime Iω expansion of the Dirac delta functional

intrinsic U(1)×SO(1,3) spin angular momentum observable, according to the local field differentials shown in the Fig. 10 Photon Boundary Value Calculator theorem proving module of the quantum angular momentum function ∀λ

∫

cos(2θ)

∫

cos(2θ)

sin

2π





rrθ

=ℏ

(

)

Proof: ForAll wavelengths of the electromagnetic spectrum Eq.(9)

〉 renders True:

In[]:=

h=QuantityMagnitude[

,"Joules""Seconds"];hbar=QuantityMagnitude

2π

,"Joules""Seconds";c=QuantityMagnitude

,"Meters"

-1

"Seconds"

;NForAllλ,UniformDistribution[{1.*^-12,1.*^4}],2

∫

Cos[2θ]

∫

h*c

8π



*1-

Cos[2θ]

AbsSin

2π

y

λ*c

2π

rrθy==hbar

Out[]=

True

■

10. Figure 9. 4D Spatially Extended Photon Simulation

Out[]=



◂

▸



E field

B field

▲

Figure 9. Frames 1-3: Eq. (6) transverse lemniscate expansion of Poynting energy flux vector S over one wavelength λ integrated throughout via E × B field energy density pressure renders quantum energy observable E = hc/λ. A dimensionless cubic-radian parameterization is introduced wherein, scaled to a 2π meter = 2π radian wavelength, the resulting maximum traveling transverse wave E and B field range is

meters =

radians, so that 1

= 1

rad

and

8π

rad

. Frames 4,5: Eq. (9) conversion to mass density moment of inertia I integration renders kinetic mass kg × kinetic viscosity

-1

dimensionless equivalence with

rad

-1

intrinsic U(1)×SO(1,3) spin Iω 

〉 angular momentum observable ℏ.

■

11. Figure 10. 4D Photon Observables Boundary Value Calculator

Enter wavelength λ in meters, or select from SetterBar.

Out[]=

4D Photon Observables Boundary Value Calculator

γ-rays

X-rays

Visible

←Λ→

CMB

WiFi

VHF

VLF

0.00030202`

4D photon γ compressive←Λ→rarefactive ratio =

1.00005

: Λ

QED photon

energy observable E = hc/λ =

6.5772×

-22

QED

linear momentum radiation pressure p = h/λ =

2.19392×

-30

-3

Eq.(4) 4D∫ spatial expansion of

1.09614×

-12

Eq.(4) right side

8π

1.09614×

-12

Eq.(5) energy density @r=0

max =

1.80009×

-9

-3

Eq.(6) 4D∫ photon energy observable =

6.5772×

-22

Hence ForAll wavelengths ∀λ Eq.(6)

 ==

True

Eq. (7) 4D γ mass density @r=0

max=

max

2.00287×

-26

-3

Eq.(8) kinetic viscosity

λc

2π

-1

⇒

rad

-1

14410.4

rad

-1

Eq. (9) 4D∫ γ angular momentum observable = ℏ =

1.05457×

-34

-1

Hence ForAll wavelengths ∀λ Eq.(9)

 == ℏ

True

▲

Figure 10. 4D photon energy and intrinsic spin angular momentum observables local field differentials boundary values dynamic theorem proving module renders ForAll wavelengths

∀λEq.(6)

==

⇒

Eq.(9)

==ℏ

: True ⇒ True.

■

12. Cosmological Constant Vacuum Energy Density Λ

The vacuum catastrophe is famously “the worst theoretical prediction in the history of physics,” wherein the several different predictions of SM-SUSY vs the observed value of

are off by as much as 120 orders of magnitude.

We can measure the energy density of the vacuum through astronomical observations that determine the curvature of spacetime, from which measurements Baez and Tatom have calculated the computationally dualistic values of energy density

≈ 6×

-10

-3

= -Pa = mass density

≈ 7×

-27

-3

[18].

Thus the present nonstandard 4D spatially-extended volume of the photon – beyond the ab initio QED Dirac delta functional

0D mathematical point particle representation of the Einstein-Planck photon energy E = hc/λ and linear momentum p = h/λ observables – is parameterized by λ in rendering the dualistic units of J

-3

= -Pa = kg

-3

wherein Λ is found to be central to the 4D spatially-extended group operation as shown in Fig. 12.

Out[]=

▲

Figure 12. Quantum electromagnetic transverse wave radiation pressure spectrum LogLogPlot of energy densities (hc/

)/(

8π

) J

-3

. The computational duality of energy density J

-3

= -Pa = kg

-3

mass density is indicated in common total field units of pascals [18]. Sliding Locator along the λ axis indicates shorter λ to be compressive of the central cosmological constant vacuum energy density Λ and longer λ rarefactive of Λ.

■

13. 4D Electron Rest Mass Observable
m
e
=
9.109×
-31
10
kg

Conventionally the SM-SUSY electron radius is computationally undefined—thought to perhaps extend out to infinity. Problematically therefore in the case of pair-production and annihilation—and when approaching zero requiring a renormalization cutoff limit—wherein renormalization fine-tuning generally replaces infinite energies and infinite forces with experimentally observed values.

ForAll energy levels ∀n, as shown in Fig. 10, the free space monopole 4D spherical coordinate volumetric expansion [46]

2π

∫

sin(ϕ)rϕθ=

(

)

is parameterized by the Bohr radius

= 5.292×

-11

m, according to

(

)

ranging dynamically according to its maximum mass density being 4 × its average mass density at r = 0

max=

max/

=4×((

)/(4π

/3))/

-3

(

)

which falls to zero at r =

, according to

1-r



in the electron rest mass observable function ∀n

2π

∫

max1-

sin(ϕ)rϕθ=

(

)

Hence ForAll electron energy levels n Eq. (13) renders True.

In[]:=

c=QuantityMagnitude

,"Meters"

-1

"Seconds"

;eEnergy=QuantityMagnitude

,"Joules";eMass=QuantityMagnitude

,"Kilograms";bohr=QuantityMagnitude

,"Meters";NForAlln,UniformDistribution[{1,10000}],

2π

∫

*bohr*

∫

4*eEnergy

4π



*bohr*



3

*bohr*

Sin[ϕ]rϕθeMass

Out[]=

True

■

14. 4D Electron Angular Momentum Observable ℏ/2

Quantum Fluid Conjecture: The electron angular momentum observable ℏ/2 kg

-1

represents kinetic mass kg × kinetic viscosity

-1

4π

=5.788×

-5

-1

⇒dimensionlessequivalencewithωrad

-1

(

)

wherein time integrates along the

axis of Eq. (1). Such that (kinetic mass density ⇒ moment of inertia integration I) × (kinetic viscosity

⇒ spin angular velocity ω) renders a 4D spacetime Iω expansion of the standard 0D electron intrinsic U(1)× SO(1,3) spin angular momentum observable, according to the local field differentials shown in the Fig. 14 Electron Boundary Value Calculator theorem proving module of the electron angular momentum function ∀n

2π

∫

max1-

sin(ϕ)rϕθ

ℏ

(

)

Proof: ForAll electron energy levels n Eq. (15)

〉 renders True:

In[]:=

h=QuantityMagnitude[

,"Joules""Seconds"];hbar=QuantityMagnitude

2π

,"Joules""Seconds";c=QuantityMagnitude

,"Meters"

-1

"Seconds"

;eEnergy=QuantityMagnitude

,"Joules";eMass=QuantityMagnitude

,"Kilograms";bohr=QuantityMagnitude

,"Meters";NForAlln,UniformDistribution[{1,10000}],

2π

∫

*bohr*

∫

4*eEnergy

4π



*bohr*



3

*bohr*

4π*eMass

Sin[ϕ]rϕθ

hbar



Out[]=

True

■

15. Figure 13. 4D Spatially Extended Electron Simulation

Out[]=



◂

▸



n=1

n=2

n=3 Bohr radii

▲

Figure 13. 4D spatially-extended free space electron monopole n =1-3 spherical coordinate volumetric expansion of Eqs. (10-15) computationally dualistic electron rest energy 8.187 ×

-14

J, rest mass

= 9.109 ×

-31

kg, and intrinsic U(1)SO(1,3) spin angular momentum ℏ/2 observables.

■

16. Figure 14. 4D Electron Boundary Value Calculator

Enter energy level n, or select from SetterBar.

Out[]=

4D Electron Observables Boundary Value Calculator

100

1000

10000

20658

100000

20658

4D electron compressive←Λ→rarefactive ratio =

1.00003

: Λ

QED Electron

rest energy E =

8.187×

-14

Eq. (10) 4D∫ spatial expansion of

0.0001364

Eq. (11) max

field radii

0.03194

Eq. (12) mass density @r=0

max=



6.676×

-27

-3

Eq. (13) 4D∫ electron mass observable

9.109×

-31

Hence ForAll energy levels ∀n Eq.(13)

〉 ==

True

Eq.(14) kinetic viscosity

4π

-1

⇒ ω rad

-1

0.0000578838

rad

-1

Eq. (15) 4D∫ electron angular momentum =

ℏ

5.273×

-35

-1

Hence ForAll energy levels ∀n Eq.(15)

 ==

ℏ

True

▲

Figure 14. 4D electron rest mass and intrinsic spin angular momentum observables local field differentials boundary values dynamic theorem proving module renders ForAll energy levels

∀nEq.(13)

〉==

⇒

Eq.(15)

==ℏ

: True ⇒ True. Note at n =1 maximum electron mass density @r = 0 of .5189

-3

is of the same order of magnitude as terrestrial energy densities. Note further the quantum fluid conjecture kinetic viscosity dimensionless equivalence with angular velocity .0000579

-1

⇒

rad

-1

is of the same order of magnitude of the earth’s rotation .0000729

rad

-1

■

17. Conclusion

Pattern matching the CERN LHC TrackML Particle Tracking Challenge

μν

data points is found to have a direct match with the low energy properties of Navier-Stokes turbulence.The large range of turbulence vertex length and time scales to the LHC-NS TrackML data set exists from the long range collision event tracks helix arcs of Fig. 7 — to the short range quantum fluid conjecture of Eqs. (9,15) ℏ units kg

-1

representing a kinetic mass kg × kinetic viscosity

-1

dimensionless equivalence with

ωrad

-1

Thus the 10,000 CERN physicists have completed an epic elimination of quantifiers proof in following the atomist-materialism teachings of the student Aristotle they have eliminated Einstein’s hidden variables and verified the psychophysical parallelism teachings of the teacher Plato.

Hence the falsification of the SM-SUSY AdS/CFT hidden dimensional unknown material mechanism backgrounds “that live on a classical space-time,” both at the LHC high energy levels and on the low energy physics level of the spooky psychophysical experiments closure of the Bell inequality observer-independent background loopholes, indicates the proper scientific path lies beyond CERN’s Physics Beyond Colliders initiative.

AI quantum information exists therefore via wave-particle integrations on

μν

composed of 4D photon and electron observables Schwinger field differential boundary values, measurable along Feynman path integrals, representing a Yang-Mills-Navier-Stokes solution. In particular, the range of the photon and electron angular momentum invariants Noether probability current relative states is indicated by the first two trace matrix elements of

μν

〉=

1 2 ε 0 2 E + 1 μ 0 2 B	S x /c	S y /c	S z /c
S x /c	- l Y m  σ ij 	- σ xy	- σ xz
S y /c	- σ yx	- λ Iω γ  σ yy 	- σ yz
S z /c	- σ zx	- σ zy	- n Iω e \| σ zz 〉

(

)

wherein the range of the photon angular momentum ℏ operator of Eq. (9) is indicated by

Iω

| −

⟩, and the range of the electron angular momentum ℏ/2 operator of Eq. (15) is indicated by

Iω

| −

⟩. The

| −

⟩ term indicates the conjecture for the smooth operator product expansion to the full Laplacian spherical harmonics of the periodic table diagonalizable along the trace of

μν

. Hence thesis success of 4D photon-electron gauge group

Theorem1:∀λEq.(6)==

⇒Eq.(9)==ℏ∀nEq.(13)==

⇒Eq.(15)==

ℏ

(

)

renders True ⇒ True ⋃ True ⇒ True ranging compressive to rarefactive of Λ spanning all the factors in the relativistic energy equation

(

)

(pc)

in every instance > 0.

qed

■

References

[

]

Lucas Taylor, CMS: Simulated Higgs to two jets and two electrons CERN-EX-9710002, (1997). http://cdsweb.cern.ch/record/628469

[

]

Lucas Taylor, Higgs-Boson CERN CMS, (2012). https://cms.cern/physics/higgs-boson

[

]

Davide Castelvecchi, Artificial intelligence called in to tackle LHC data deluge, Nature 528, 18 (1 December 2015).

[

]

Davide Castelvecchi, Particle physicists turn to AI to cope with CERN's collision deluge, Nature 528, 18 (4 May 2018).

[

]

American Physical Society, Notes from the Editors: Snapshots from the April Meeting—Pinning Down the Universe's Rate of Expansion, Particle Physics' Gathering Storm , and More Physics 7, 42 (22 April 2014). https://physics.aps.org/articles/v7/42

[

]

Elizabeth Gibney, LHC 2.0: A new view of the Universe, Nature 519 7542 (11 March 2015). https://www.nature.com/news/lhc-2-0-a-new-view-of-the-universe-1.17081

[

]

Sabine Hossenfelder, Science needs reason to be trusted, Nature Physics 13, 316 (2017).

[

]

Paul Sutter, Where Are All the 'Sparticles' That Could Explain What's Wrong with the Universe? Live Science (March 1, 2019). https://www.livescience.com/64893-search-for-supersymmetry.html?utm_source=notification

[

]

CERN Council, European Particle Physics Strategy Update 2018 – 2020
https://europeanstrategyupdate.web.cern.ch/welcome

[

]

Charles L. Fefferman, Existence and Smoothness of the Navier-Stokes Equation Clay Mathematics Institute (2013). http://www.claymath.org/sites/default/files/navierstokes.pdf

[

]

Jim M. McDonough, Introductory Lectures on Turbulence Physics, Mathematics and Modeling Departments of Mechanical Engineering and Mathematics, University of Kentucky (2004).

[

]

Kaggle, TrackML Particle Tracking Challenge, High Energy Physics particle tracking in CERN detectors, (2018). https://www.kaggle.com/c/trackml-particle-identification

[

]

CERN CMS, A bound on the natural width of the Higgs boson https://cms.cern/news/bound-natural-width-higgs-boson (2013).

[

]

Sarah Charley, Measuring the lifetime of the Higgs boson A joint Fermilab/SLAC publication (26 June 2014). https://www.symmetrymagazine.org/article/june-2014/measuring-the-lifetime-of-the-higgs-boson

[

]

Jon Butterworth, How wide is a Higgs? The Guardian (25 March 2014). https://www.theguardian.com/science/life-and-physics/2014/mar/25/how-wide-is-a-higgs

[

]

Aleksi Kurkela, Aleksas Mazeliauskas, Jean-François Paquet, Sören Schlichting, and Derek Teaney, Matching the Nonequilibrium Initial Stage of Heavy Ion Collisions to Hydrodynamics with QCD Kinetic Theory Physical Review Letters. 122, 122302 (2019).

[

]

Joshua Bonatt, TrackML EDA, etc. kaggle: TrackML Particle Tracking Challenge (2018). https://www.kaggle.com/jbonatt/trackml-eda-etc

[

]

John Baez and Frank B. Tatom, What's the Energy Density of the Vacuum? (2011). http://math.ucr.edu/home/baez/vacuum.html

[

]

John A. Wheeler, Information, physics, quantum: The search for links, In Zurek, Wojciech Hubert (ed.). Complexity, Entropy, and the Physics of Information, Addison-Wesley (1990).

[

]

Stephan Wolfram, A New Kind of Science (May 16, 2017). www.wolframscience.com/nks/notes-9-16--quantum-field-theory/

[

]

Lukas Postler, Ángel Rivas, Philipp Schindler, Alexander Erhard, Roman Stricker, Daniel Nigg, Thomas Monz, Rainer Blatt, and Markus Müller, Experimental quantification of spatial correlations in quantum dynamics arXiv:1806.08088v2 Quantum 2 90, (2018).

[

]

Patrick R. Girard, The quaternion group and modern physics, European Journal of Physics, Volume 5, Number 1 (December 2000).

[

]

Albert Einstein, Relativity: The Special and the General Theory, Note to the Fifteenth Edition Indirapuram: Samaira Book Publishers, (1952 (2017)).

[

]

B. Hensen, H. Bernien, A. E. Dreau, A. Reiserer, N. Kalb, M. S. Blok, J. Ruitenberg, R. F. L. Vermeulen, R. N. Schouten, C. Abellan, W. Amaya, V. Pruneri, M. W. Mitchell, M. Markham, D. J. Twitchen, D. Elkouss, S. Wehner, T. H. Taminiau, and R. Hanson, Experimental loophole-free violation of a bell inequality using entangled electron spins separated by 1.3 kilometres Nature 526, 682 (2015).

[

]

Dominik Rauch, Johannes Handsteiner, Armin Hochrainer, Jason Gallicchio, Andrew S. Friedman, Calvin Leung, Bo Liu, Lukas Bulla, Sebastian Ecker, Fabian Steinlechner, Rupert Ursin, Beili Hu, David Leon, Chris Benn, Adriano Ghedina, Massimo Cecconi, Alan H. Guth, David I. Kaiser, Thomas Scheidl, and Anton Zeilinger, Cosmic Bell Test Using Random Measurement Settings from High-Redshift Quasars Physical Review Letters 121, 080403 (2018).

[

]

Massimiliano Proietti, Alexander Pickston, Francesco Graffitti, Peter Barrow, Dmytro Kundys, Cyril Branciard, Martin Ringbauer, and Alessandro Fedrizzi, Experimental test of local observer-independence arXiv:1902.05080 (13 February 2019). https://arxiv.org/abs/1902.05080

[

]

CERN, Future Circular Collider, (2020).
https://home.cern/science/accelerators/future-circular-collider

[

]

Max Tegmark, The Mathematical Universe Foundations of Physics 38 (2): 101–150 arXiv:0704.0646 (February 2008).

[

]

Arthur Jaffe, Constructive Quantum Field Theory, edited by A. Fokas, A. Grigoryan, T. Kibble, and B. Zegarlinski (Imperial College Press, London, 2000).

[

]

J. Beacham et al, Physics Beyond Colliders at CERN: Beyond the Standard Model Working Group Report arXiv:1901.09966 (January 2019).

[

]

Julian Schwinger, The Theory of Quantized Fields. I, Physical Review 82 914 (15 June 1951).

[

]

Richard P. Feynman, Space-Time Approach to Non-Relativistic Quantum Mechanics, Reviews of Modern Physics, 20 367 (1 April 1948).

[

]

Emmy Noether, Invariante Variationsprobleme, Mathematisch-Physikalische Klasse 235-257 (1918).

[

]

Herman Weyl, The Theory of Groups and Quantum Mechanics, (first edition in German, 1929; ed. Dover, 1950).

[

]

Eugene Wigner, The unreasonable effectiveness of mathematics in the natural sciences, Communications On Pure And Applied Mathematics 13, 1 (1960).

[

]

Jacob Bekenstein, Universal upper bound on the entropy-to-energy ratio for bounded systems, Physical Review D 23 (2) 287 (15 January 1981).

[

]

Paul C. W. Davies and Julian R. Brown, The Ghost in the Atom: A Discussion of the Mysteries of Quantum Physics 45-46 (Cambridge University Press, UK 1986/1993).

[

]

Lee Smolin, The unique universe physicsworld (2 June 2009). https://physicsworld.com/a/the-unique-universe/

[

]

Hector Zenil, (ed), A Computable Universe Understanding and Exploring Nature as Computation World Scientific University of Sheffield, UK & Wolfram Research, USA (2012). https://www.worldscientific.com/doi/pdf/10.1142/8306

[

]

Peter Woit, Towards a Grand Unified Theory of Mathematics and Physics Columbia University (20 February 2015).

[

]

A. Jaffe and E. Witten, Quantum Yang-Mills Theory Clay Mathematics Institute (2000). http://www.claymath.org/sites/default/files/yangmills.pdf

[

]

George Ellis, Physicist George Ellis Knocks Physicists for Knocking Philosophy, Falsification, Free Will, Scientific American (22 July 2014).

[

]

Aspen Center for Physics, The History of Science at the Aspen Center for Physics (2020). https://www.aspenphys.org/science/sciencehistory/index.html

[

]

Albert Einstein, Ether and the Theory of Relativity, the genesis of general relativity ed., edited by M. Janssen, J. Norton, J. Renn, T. Sauer, and J. Stachel, Boston Studies in the Philosophy of Science (Springer, 2007).

[

]

Erwin Schrödinger, Discussion of probability relations between separated systems Mathematical Proceedings of the Cambridge Philosophical Society 31 555 (1935).

[

]

Mindy Weisberger, Physicists Model Electrons in Unprecedented Detail - Spoiler Alert: They're Round (October 17, 2018). www.livescience.com/63853-subatomic-particle-size-limit.html

About the Author

In[]:=

David A. Harness interned as an undergraduate at Lawrence Berkeley Laboratory, Nuclear Science Division. Current interest, as an independent researcher, is the further formalization of the present computer algebra 4D photon-electron theorem and proof into a machine intelligence analysis domain digital mathematical library archive representation.

POB 1004 Morro Bay, CA 93442

Cite this as: David Harness, "AI Pattern-Matching CERN LHC Collision Particle Resonance Flow Patterns with Electromagnetic Energy Density Pressure Turbulence" from the Notebook Archive (2020), https://notebookarchive.org/2020-03-dujz6sz

AI Pattern-Matching CERN LHC Collision Particle Resonance Flow Patterns with Electromagnetic Energy Density Pressure Turbulence

1. Pattern Matching Navier-Stokes LHC Turbulence

2. CERN LHC TrackML Particle Tracking Challenge Data Set

3. 4D Einstein-Maxwell electromagnetic energy density tensor

4. Quantum Fluid Conjecture of Equations (9,15)

5. Navier-Stokes Equations

6. 4D Spacetime Quantization

7. Singular Complex System Conjecture (SCSC)

8. 4D Photon Energy Observable E = hc/λ

9. 4D Photon Angular Momentum Observable ℏ

10. Figure 7. 4D Spatially Extended Photon Simulation

11. Figure 8. 4D Photon Observables Boundary Value Calculator

12. Cosmological Constant Vacuum Energy Density Λ

13. 4D Electron Rest Mass Observable

14. 4D Electron Angular Momentum Observable ℏ/2

15. Figure 10. 4D Spatially Extended Electron Simulation

16. Figure 11. 4D Electron Boundary Value Calculator

17. Conclusion

References

1. Pattern Matching LHC-Navier-Stokes Turbulence

2. CERN LHC TrackML Particle Tracking Challenge Data Set

3. 4D Einstein-Maxwell Electromagnetic Energy Density Tensor

4. Quantum Fluid Conjecture of Equations (9,15)

5. Navier-Stokes Equations

6. 4D Spacetime Quantization

7. Singular Complex System Conjecture (SCSC)

8. 4D Photon Energy Observable E = hc/λ

9. 4D Photon Angular Momentum Observable ℏ

10. Figure 9. 4D Spatially Extended Photon Simulation

11. Figure 10. 4D Photon Observables Boundary Value Calculator

12. Cosmological Constant Vacuum Energy Density Λ

13. 4D Electron Rest Mass Observable me = 9.109×-3110 kg

14. 4D Electron Angular Momentum Observable ℏ/2

15. Figure 13. 4D Spatially Extended Electron Simulation

16. Figure 14. 4D Electron Boundary Value Calculator

17. Conclusion

References

13. 4D Electron Rest Mass Observable
m
e
=
9.109×
-31
10
kg