Comparing Expansion in Physical and Branchial Space
Author
Manojna Namuduri
Title
Comparing Expansion in Physical and Branchial Space
Description
Does the Wolfram physics framework reveal a relationship between increasingly entangled quantum degrees of freedom and the emergence of spacetime geometry in the early Universe?
Category
Essays, Posts & Presentations
Keywords
Inflationary cosmology, quantum gravity, quantum information, holographic principle, AdS/CFT correspondence, branchial space
URL
http://www.notebookarchive.org/2020-07-6hj45x0/
DOI
https://notebookarchive.org/2020-07-6hj45x0
Date Added
2020-07-14
Date Last Modified
2020-07-14
File Size
306.88 megabytes
Supplements
Rights
Redistribution rights reserved

WOLFRAM SUMMER SCHOOL 2020
Comparing Expansion in Physical and Branchial Space
Comparing Expansion in Physical and Branchial Space
Manojna Namuduri
Minerva Schools at Keck Graduate Institute, Class of 2020
The main goal of this project is to identify correlations between the growths of spatial hypergraphs and their associated branchial graphs. If there is a relationship between the sizes or the geometries of these graph counterparts as they evolve in time, then that relationship can provide insight as to how continuing entanglement of quantum degrees of freedom supports the emergence of spacetime geometry in early Universe expansion. The findings of this project can ultimately be used to probe quantum theories of gravity built on the holographic principle.
Wolfram Community Post
Wolfram Community Post
Motivation One of the holy grail goals for a fundamental theory of physics is the reconciliation of general relativity and quantum field theory, two domains that describe our Universe at vastly different scales. Quantum theories of gravity, such as the popular conjecture of anti-de Sitter/conformal field theory (AdS/CFT) correspondence, rely on the holographic principle. In a holographic Universe, quantum laws operating on the three-dimensional boundary of spacetime are equivalent to the gravitational regime defining the geometry of the four-dimensional interior of the Universe (Ramallo, 2013). For every entity on the spacetime boundary, there is a correspondence to some entity in the interior.
In an attempt to illustrate how holographic space could emerge, Bao et al. used a quantum circuit to simulate early cosmological inflation (2017a). In this model, increasing entanglement of quantum degrees of freedom results in expansion of a comoving region of space, as measured by its de Sitter entropy. The mechanics of such a quantum circuit cosmology seem to coincide with certain aspects of the Wolfram physics framework. A branchial graph is an instantaneous map of entanglements between quantum states; in other words, branchial space contains the common ancestry of different hypergraph updates at a given time step. Presumably, in the limit of a large enough multiway system, the branchial space would grow to resemble a high- or infinite-dimensional complex projective Hilbert space that would contain the quantum mechanics of the Universe (Wolfram, 2020). Naturally, Wolfram hypergraphs are a discrete model of physical space. The pertinent question for this project is therefore whether there are correlations between the growth of a hypergraph and its respective branchial graph.
In an attempt to illustrate how holographic space could emerge, Bao et al. used a quantum circuit to simulate early cosmological inflation (2017a). In this model, increasing entanglement of quantum degrees of freedom results in expansion of a comoving region of space, as measured by its de Sitter entropy. The mechanics of such a quantum circuit cosmology seem to coincide with certain aspects of the Wolfram physics framework. A branchial graph is an instantaneous map of entanglements between quantum states; in other words, branchial space contains the common ancestry of different hypergraph updates at a given time step. Presumably, in the limit of a large enough multiway system, the branchial space would grow to resemble a high- or infinite-dimensional complex projective Hilbert space that would contain the quantum mechanics of the Universe (Wolfram, 2020). Naturally, Wolfram hypergraphs are a discrete model of physical space. The pertinent question for this project is therefore whether there are correlations between the growth of a hypergraph and its respective branchial graph.
Methods I started to answer this question by sampling rules of signature → , which is the simplest signature that can lead to unbounded growth in a hypergraph. I selected only the rules that demonstrated continued growth and filtered according to whether the rules resulted in connected or disconnected hypergraphs. Additionally, I analyzed some rules of signature → , which I knew would generate lattices underlying emergent geometries — manifolds (Wolfram, 2020). For each rule, I visualized states, plotted growth of graph nodes/edges and growth of neighborhood volumes, and compared the subgraph distributions of the final states for both physical and branchial space. I also considered the transitive reduction of branchial space and used programmatic fitting (linear, logistic, exponential, logarithmic, polynomial) to generalize and compare growth in physical and branchial space. Lastly, I wrote a pipeline to analyze initial condition effects on branchial volume and initial condition/update scheme effects on hypergraph volume for a particular rule.
2
2
3
2
2
3
3
3
Results In general, branchial space grows faster than physical space. When physical and branchial growth of edges/nodes is compared on a log-log plot, most rules demonstrate a higher slope for the branchial growth. But there are some cases where there is no branchial growth, or when the size of branchial space fluctuates or remains constant — it would be worth exploring heuristics for when this happens.
From my analysis of connected → rules, I found that rules with line-like and radial hypergraph behavior tend to have dull branchial dynamics. Line-like or radial rules that demonstrate no branchial growth tend to be highly symmetrical, which makes sense as there would little ambiguity or a high degree of isomorphism in applications of the update rule. Below are visuals of line-like rules that have more interesting branchial dynamics.
From my analysis of connected
2
2
3
2
Figure 1. Physical/branchial plots for a line-like hypergraph with exponential (instead of linear) growth of edges/nodes.
In[]:=
GraphicsGridWolframModel[{{1,2},{2,3}}{{1,4},{4,5},{3,5}},{{0,0},{0,0}},6,"StatesPlotsList"][[2;;7]],TableGraphResourceFunction["MultiwaySystem"]
[{{1,2},{2,3}}{{1,4},{4,5},{3,5}}],{{{0,0},{0,0}}},t,"BranchialGraphStructure",ImageSizeSmall,{t,1,6}
|
Out[]=

Figure 2. Physical/branchial plots for a line-like hypergraph with corresponding branchial space that has increasingly more subgraphs of varying complexity.
In[]:=
GraphicsGridWolframModel[{{1,2},{3,2}}{{1,4},{4,3},{5,3}},{{0,0},{0,0}},7,"StatesPlotsList"][[2;;8]],TableGraphResourceFunction["MultiwaySystem"]
[{{1,2},{3,2}}{{1,4},{4,3},{5,3}}],{{{0,0},{0,0}}},t,"BranchialGraphStructure",ImageSizeSmall,{t,1,7}
|
Out[]=

From my analysis of disconnected → rules, I have not yet been able to understand why some disconnected rules generate branchial space growth while others do not. In general, I have noticed that rules with no branchial growth create less complex hypergraphs — and yet, there are rules that do demonstrate branchial growth that have similarly simple hypergraphs. I would say that the morphology of disconnected hypergraphs includes those with only simple repetitive structures, those with one main subgraph of increasing complexity, and rules featuring subgraphs of varying complexity. Examples of the latter two types and their corresponding branchial growth are shown below.
2
2
3
2
Figure 3. Physical/branchial plots for a disconnected hypergraph with one main subgraph that seems to be slowly knitting a lattice in branchial space.
In[]:=
GraphicsGridWolframModel[{{1,2},{2,3}}{{4,4},{4,3},{2,3}},{{0,0},{0,0}},6,"StatesPlotsList"][[2;;7]],TableGraphResourceFunction["MultiwaySystem"]
[{{1,2},{2,3}}{{4,4},{4,3},{2,3}}],{{{0,0},{0,0}}},t,"BranchialGraphStructure",ImageSizeSmall,{t,1,6}
|
Out[]=

Figure 4. Physical/branchial plots for a disconnected hypergraph with subgraphs of (varying) increasing complexity.
In[]:=
GraphicsGridWolframModel[{{1,2},{2,3}}{{2,3},{2,4},{3,4}},{{0,0},{0,0}},7,"StatesPlotsList"][[2;;8]],TableGraphResourceFunction["MultiwaySystem"]
[{{1,2},{2,3}}{{2,3},{2,4},{3,4}}],{{{0,0},{0,0}}},t,"BranchialGraphStructure",ImageSizeSmall,{t,1,7}
|
Out[]=

All of the manifold-generating rules I considered had signature → . They all generated hypergraphs with linear growth of nodes/edges and roughly polynomial neighborhood growth. All the rules that demonstrated branchial growth showed exponential growth of disconnected subgraphs, which was the most common behavior in the sample. The manifold-generating rules were the most amenable to the subgraph analysis, and I noticed two general trends. When branchial structures were more complex, there tended to be shared subgraphs between branchial and physical space. When branchial structures were simpler (usually in the context of disconnected branchial graphs), physical subgraphs tended to be more complex. It remains to be seen whether these trends generalize to a broader set of rules and why they might exist.
2
3
3
3
Figure 5. Subgraph distributions of the branchial and physical graphs for the same rule depicted in the header images at time step 8.
In[]:=
subgraphdist[ResourceFunction["HypergraphToGraph"][WolframModel[{{x,x,y},{y,z,u}}{{v,v,u},{v,u,x},{z,y,v}},{{0,0,0},{0,0,0}},8,"FinalState"]]]subgraphdistGraphResourceFunction["MultiwaySystem"]
[{{x,x,y},{y,z,u}}{{v,v,u},{v,u,x},{z,y,v}}],{{0,0,0},{0,0,0}},8,"BranchialGraphStructure"subgraphdistTransitiveReductionGraphGraphResourceFunction["MultiwaySystem"]
[{{x,x,y},{y,z,u}}{{v,v,u},{v,u,x},{z,y,v}}],{{0,0,0},{0,0,0}},8,"BranchialGraphStructure"
|
|
Out[]=
 2,
2, 1,
1, 1,
1, 1,
1, 1,
1, 1,
1, 1,
1, 1,
1, 1,
1, 1,
1, 1,
1, 1,
1, 1,
1, 1
1
Out[]=
 108,
108, 65,
65, 22,
22, 14,
14, 14,
14, 13,
13, 3,
3, 3
3
Out[]=
 164,
164, 42,
42, 34,
34, 2
2
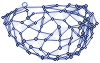
Below I have included visualizations of two manifolds that seem to resemble de Sitter and anti-de Sitter space. These are two solutions to the Einstein field equations used in the context of holographic quantum gravitational theories. The first rule, which has a spherical-looking hypergraph, represents a de Sitter Universe that is empty, highly symmetrical, has a positive cosmological constant (accelerating expansion), and has positive curvature. The second rule looks like anti-de Sitter space, which is also empty and symmetrical, but instead has a negative cosmological constant (decelerating expansion) and negative curvature, as exemplified by the saddle-like shape and hyperbolic geometry (there are increasingly more nodes closer to the boundary of the space). Sadly, these rules demonstrated little to no branchial growth, which is not conducive to our expectation of a developing Hilbert space.
Figure 6. Physical and branchial evolution for a rule that seems to approximate de Sitter space.
WolframModelPlot[WolframModel[{{x,y,y},{x,z,u}}{{u,v,v},{v,z,y},{x,y,v}},{{0,0,0},{0,0,0}},#,"FinalState"],ImageSizeTiny]&/@{100,200,400,800}GraphicsGridWolframModel[{{x,y,y},{x,z,u}}{{u,v,v},{v,z,y},{x,y,v}},{{0,0,0},{0,0,0}},6,"StatesPlotsList"][[2;;7]],TableGraphResourceFunction["MultiwaySystem"]
[{{x,y,y},{x,z,u}}{{u,v,v},{v,z,y},{x,y,v}}],{{{0,0,0},{0,0,0}}},t,"BranchialGraphStructure",ImageSizeSmall,{t,1,6}
|
Out[]=
 ,
, ,
, ,
,




Out[]=
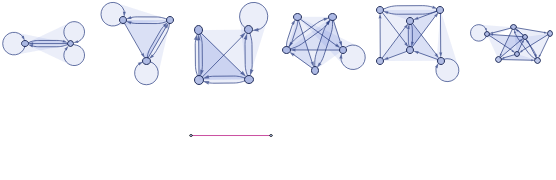
Figure 7. Physical and branchial evolution for a rule that seems to approximate anti de Sitter space.
In[]:=
WolframModelPlot[WolframModel[{{x,y,x},{x,z,u}}{{u,v,u},{v,u,z},{x,y,v}},{{0,0,0},{0,0,0}},#,"FinalState"],ImageSizeTiny]&/@{100,200,400,800}GraphicsGridWolframModel[{{x,y,x},{x,z,u}}{{u,v,u},{v,u,z},{x,y,v}},{{0,0,0},{0,0,0}},6,"StatesPlotsList"][[2;;7]],TableGraphResourceFunction["MultiwaySystem"]
[{{x,y,x},{x,z,u}}{{u,v,u},{v,u,z},{x,y,v}}],{{{0,0,0},{0,0,0}}},t,"BranchialGraphStructure",ImageSizeSmall,{t,1,6}
|
Out[]=
 ,
, ,
, ,
,




Out[]=

There is clearly still a lot to learn about the correlations between evolving physical and branchial space. Here are a couple of ideas I have on how to extend and improve the work done so far:
◼
Continued subgraph analysis on longer evolutions of branchial space. This is computationally expensive, but being able to look at branchial evolution at greater times is necessary, as physical structure slowly builds as the hypergraph evolves through time.
◼
Analysis of branchial/hypergraph volume variance. The pipeline I wrote worked, but I did not do much beyond generating some plots and descriptive statistics with it. Also considering branchial volume variance from the additional parameter of possible foliations in the multiway systems, which represent different quantum observation frames.
◼
Another useful metric for comparing physical and branchial space might be entropy. de Sitter entropy is supposed to be proportional to the size of physical space, whereas entanglement entropy would probably describe the degree of connectivity in branchial space (Ryu & Takayanagi, 2006). How might these quantities be defined in the Wolfram physics framework?
◼
Better metric(s) for characterizing growth in disconnected graphs, both physical and branchial.
◼
Tensor networks seem to have been a successful way to represent highly entangled quantum many-body systems (Orus, 2014; Bao et al., 2017b). How could this mathematical object be understood in the context of branchial space? Are tensor representations of branchial connectivity related to the geometry of hypergraphs?
◼
Considering Friedmann-Lemaitre-Robertson-Walker Universes, which are homogeneous, isotropic, expanding, and filled with matter, like our Universe. What rules would satisfy the FLRW metric/fit in with Lambda-CDM cosmology? What does a holographic theory look like for this Einstein field equation solution, as opposed to the anti de Sitter/de Sitter solutions usually considered?
◼
Some quantum information theorists have thought about how holographic anti de Sitter spacetime could emerge from boundary physics featuring a quantum error correction code, which would produce black holes when it fails to correct errors (Almheiri et al., 2015; Wolchover, 2019a). To explore this possibility, it would be interesting to look at rules that result in disconnected physical and branchial space, a quality that could indicate the presence of black holes (Wolfram, 2020).
Complete project work
Complete project work
Keywords
Keywords
Acknowledgment
Acknowledgment
References
References
Cite this as: Manojna Namuduri, "Comparing Expansion in Physical and Branchial Space" from the Notebook Archive (2020), https://notebookarchive.org/2020-07-6hj45x0
Download

