Working Material

Graph algorithms

Vojtěch (Vojtech) Bartík (Bartik)

Author

Vojtěch (Vojtech) Bartík (Bartik)

Title

Graph algorithms

Description

Defines functions realizing some well known algorithms for simple graphs (or their modifications) and producing not only expected results but also tables (and in some cases also animations) helping to understand how these algorithms work.

Graph Algorithms

Demo

Vojtěch Bartík, February 2021

Convention : All graphs are supposed simple without loops. Vertices are positive natural numbers and all edges are supposed to be directed or undirected.

In[]:=

Off[EdgeWeightedGraphQ::argx,General::argx,Graph::supp,Unset::norep];

Axiliary Definitions

EdgeListQ[E]
returns True if
E
may be considered as the EdgeList of a directed or undirected graph in the sense of Mathematica, and False in the opposite case.
EdgeListQ[E,∞]
returns True if
Graph[E]
is undirected graph in the sense of Mathematica and False in the opposite case.


WeightedEdgeListQ[E]
returns True if
First/@E
may be considered as the EdgeList of a directed or undirected graph with the
EdgeWeightLast/@E
in the sense of Mathematica, and False in the opposite case.
WeightedEdgeListQ[E,∞]
returns True if
Graph[First/@E,EdgeWeight->Last/@E]
is the undirected graph in the sense of Mathematica, and False in the opposite case.


WeightedAdjacencyMatrixQ[M]
returns True if
M
is a square matrix with numeric entries and zeros on the diagonal, and False in the opposite case.
WeightedAdjacencyMatrixQ[M,∞]
returns True if
M
is a symmetric square matrix with numeric non-diagonal entries and
∞
’s on the diagonal, and False in the opposite case.


ToEdgeList


ToWeightedEdgeList


ToWeightedAdjacencyMatrix


ToGraph


ToEdgeWeightedGraph


Random EdgeLists, Matrices and Graphs

RandomEdgeList, RandomWeightedEdgeList


RandomWeightedAdjacencyMatrix


RandomAcyclicGraph


Components

Example 1

In[]:=

V8=Range[1,10];E8={{2,3},{3,4},{4,3},{5,9},{6,8},{7,8},{7,10},{8,10}};gE8=ToGraph[E8,EdgeShapeFunctionGraphElementData[{"Arrow","ArrowSize".05}],DirectedEdgesTrue,VertexLabels"Name",VertexSize0.1,VertexStyleRed,ImagePadding20,GraphLayoutAutomatic,VertexCoordinatesEllipse[6,3,10]]

Out[]=

In[]:=

{AdjacentVertices[gE8,#,-1]&/@V8,AdjacentVertices[gE8,#,1]&/@V8,AdjacentVertices[E8,#,0]&/@V8,AdjacentVertices[E8,#]&/@V8}//Column[#,Center,Spacings1]&

Out[]=

{{},{},{2,4},{3},{},{},{},{6,7},{5},{7,8}}

{{},{3},{4},{3},{9},{8},{8,10},{10},{},{}}

{{},{3},{2,4},{3},{9},{8},{8,10},{6,7,10},{5},{7,8}}

In[]:=

{AccesibleVertices[gE8,#,-1]&/@V8,AccesibleVertices[gE8,#,1]&/@V8,AccesibleVertices[E8,#,0]&/@V8,AccesibleVertices[E8,#]&/@V8}//Column[#,Center,Spacings1]&

Out[]=

{{1},{2},{2,3,4},{2,3,4},{5},{6},{7},{6,7,8},{5,9},{6,7,8,10}}

{{1},{2,3,4},{3,4},{3,4},{5,9},{6,8,10},{7,8,10},{8,10},{9},{10}}

{{1},{2,3,4},{2,3,4},{2,3,4},{5,9},{6,7,8,10},{6,7,8,10},{6,7,8,10},{5,9},{6,7,8,10}}

In[]:=

{Components@E8,Components@gE8,StrongComponents@E8//Sort,ConnectedComponents@gE8//Sort}//Column[#,Center]&

Out[]=

{{1},{2,3,4},{5,9},{6,7,8,10}}

{{1},{2},{5},{6},{7},{8},{9},{10},{3,4}}

Example 2

In[]:=

V9=Range[13];E9={{1,3},{1,11},{2,6},{3,9},{4,12},{5,7},{6,10},{7,13},{9,11}};gE9∞=ToGraph[E9,∞,ImagePadding20,GraphLayoutAutomatic,VertexLabels"Name",VertexSize0.15,VertexStyleRed,VertexCoordinatesEllipse[6,3,13]]

Out[]=

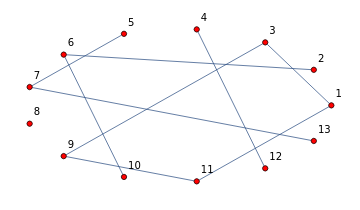
In[]:=

{AdjacentVertices[gE9∞,#,-1]&/@V9,AdjacentVertices[gE9∞,#,1]&/@V9,AdjacentVertices[E9,#,0]&/@V9,AdjacentVertices[E9,#]&/@V9}//Column[#,Center,Spacings1]&

Out[]=

{{},{},{1},{},{},{2},{5},{},{3},{6},{1,9},{4},{7}}

{{3,11},{6},{9},{12},{7},{10},{13},{},{11},{},{},{},{}}

{{3,11},{6},{1,9},{12},{7},{2,10},{5,13},{},{3,11},{6},{1,9},{4},{7}}

In[]:=

{AccesibleVertices[gE9∞,#,-1]&/@V9,AccesibleVertices[gE9∞,#,1]&/@V9,AccesibleVertices[gE9∞,#,0]&/@V9,AccesibleVertices[gE9∞,#]&/@V9}//Column[#,Center,Spacings1]&

Out[]=

{{1},{2},{1,3},{4},{5},{2,6},{5,7},{8},{1,3,9},{2,6,10},{1,3,9,11},{4,12},{5,7,13}}

{{1,3,9,11},{2,6,10},{3,9,11},{4,12},{5,7,13},{6,10},{7,13},{8},{9,11},{10},{11},{12},{13}}

{{1,3,9,11},{2,6,10},{1,3,9,11},{4,12},{5,7,13},{2,6,10},{5,7,13},{8},{1,3,9,11},{2,6,10},{1,3,9,11},{4,12},{5,7,13}}

In[]:=

{Components@E9,Components@gE9∞,ConnectedComponents@gE9∞}//Column[#,Center]&

Out[]=

{{1,3,9,11},{2,6,10},{4,12},{5,7,13},{8}}

{{1,3,11,9},{5,7,13},{6,2,10},{12,4},{8}}

In[]:=

{StrongComponents@E9//Sort,ConnectedComponents@ToGraph[E9]//Sort}//Column[#,Center]&

Out[]=

{{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13}}

Minimal Spanning Tree

Options

Alternatives for optional arguments of Jarnik-Prim’ algorithm: -- Dividers -> {{Thin,Thin,{Dotted},Thin,Thin},Thin} | any admissible data,-- FrameColor → Red,-- GraphLayout  Automatic | any Graph layout, -- ImagePadding -> 10 | any number,-- ImageSize -> Automatic | {450, 150} | any size,-- ItemColor → Green | any color,-- SelectionRule -> First | Last | RandomChoice,-- ShowTree -> True | False,-- Sort -> False | True,-- Spacings → {1, 1} | any pair of positive numbers | Automatic,-- Trace  True | False,-- Tree  True | False,-- TreeEdgeStyle  {Thickness[0.004], Red} | any admissible Graph EdgeStyle,-- VertexCoordinates  Automatic | Ellipse[a, b] ,-- VertexLabels -> “Name” | any admissible Graph VertexLabels,-- VertexLabelStyle  Directive[Blue, 10, Bold] | any admissible Graph VertexLabelStyle.-- VertexSize -> Tiny | Automatic | Small | Medium | Large | number | {“Scaled”, number},-- VertexStyle  Blue | any color.

In[]:=

Options[JarnikPrimTree]

Out[]=

Dividers{{Thickness[Tiny],Thickness[Tiny],{Dashing[{0,Small}]},Thickness[Tiny],Thickness[Tiny]},Thickness[Tiny]},FrameColor

,GraphLayoutAutomatic,ImagePadding10,ImageSizeAutomatic,ItemColor

,SelectionRuleFirst,ShowTreeTrue,SortFalse,Spacings{0.7,0.7},TraceTrue,TreeTrue,TreeEdgeStyleThickness[0.004],

,VertexCoordinatesAutomatic,VertexLabelsName,VertexLabelStyleDirective

,10,Bold,VertexSizeTiny,VertexStyle



Alternatives for optional arguments of Borůvka-Kruskal’s algorithm -- AdjustedEdgeList → True, -- GraphLayout  Automatic | any Graph layout,-- ImagePadding -> 10 | any number,-- ImageSize -> Automatic | {450, 150} | any size,-- SelectionRule -> First | Last | RandomChoice,-- ShowTree -> True | False,-- Sort -> False | True,-- Spacings → {1, 1} | any pair of positive numbers | Automatic,-- Trace  True | False,-- Tree  True | False,-- TreeEdgeStyle  {Thickness[0.004], Red} | any admissible Graph EdgeStyle,-- VertexCoordinates  Automatic | Ellipse[a, b],-- VertexLabels -> “Name” | any admissible Graph VertexLabels,-- VertexLabelStyle  Directive[Blue, 10, Bold] | any admissible Graph VertexLabelStyle,-- VertexSize -> Tiny | Automatic | Small | Medium | Large | number | {“Scaled”, number},-- VertexStyle  Blue | any color.

In[]:=

Options[BoruvkaKruskalTree]

Out[]=

AdjustedEdgeListTrue,GraphLayoutAutomatic,ImagePadding10,ImageSizeAutomatic,SelectionRuleFirst,ShowTreeTrue,SortFalse,Spacings{0.7,0.7},TraceTrue,TreeTrue,TreeEdgeStyleThickness[0.004],

,VertexCoordinatesAutomatic,VertexLabelsName,VertexLabelStyleDirective

,10,Bold,VertexSizeTiny,VertexStyle



Example 3

In[]:=

M1=

∞	8	2	2	9	2
8	∞	-5	-1	∞	19
2	-5	∞	-5	3	14
2	-1	-5	∞	3	-2
9	∞	3	3	∞	2
2	19	14	-2	2	∞

;

In[]:=

EM1=ToWeightedEdgeList[M1];gM1=ToEdgeWeightedGraph[M1];Column[{EM1,gM1,EdgeList[gM1],Options[gM1,EdgeWeight]},Center,Spacings1]

Out[]=

{{{1,2},8},{{1,3},2},{{1,4},2},{{1,5},9},{{1,6},2},{{2,3},-5},{{2,4},-1},{{2,6},19},{{3,4},-5},{{3,5},3},{{3,6},14},{{4,5},3},{{4,6},-2},{{5,6},2}}

Graph

Vertex count: 6

Edge count: 14



{12,13,14,15,16,23,24,26,34,35,36,45,46,56}

{EdgeWeight{8,2,2,9,2,-5,-1,19,-5,3,14,3,-2,2}}

In[]:=

JarnikPrimTree[EM1,1]

{{{1,3},2},{{3,2},-5},{{3,4},-5},{{4,6},-2},{{6,5},2}}

Total Weight-8

★

Selected Edge

★

{1,3}2

★

-5

★

-5

{3,2}-5

★

-5

{3,4}-5

★

-2

{4,6}-2

★

{6,5}2

In[]:=

JarnikPrimTree[gM1,1,ShowTreeFalse];

{{{1,3},2},{{3,2},-5},{{3,4},-5},{{4,6},-2},{{6,5},2}}

Total Weight-8

★

Selected Edge

★

{1,3}2

★

-5

★

-5

{3,2}-5

★

-5

{3,4}-5

★

-2

{4,6}-2

★

{6,5}2

In[]:=

JarnikPrimTree[gM1,1,ShowTreeFalse,TraceFalse];

{{{1,3},2},{{3,2},-5},{{3,4},-5},{{4,6},-2},{{6,5},2}}

Total Weight-8

In[]:=

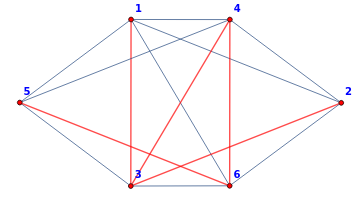
BoruvkaKruskalTree[M1];

{{{2,3},-5},{{3,4},-5},{{4,6},-2},{{1,3},2},{{5,6},2}}

Total Weight-8

{{{2,3},-5},{{3,4},-5},{{4,6},-2},{{2,4},-1},{{1,3},2},{{1,4},2},{{1,6},2},{{5,6},2},{{3,5},3},{{4,5},3},{{1,2},8},{{1,5},9},{{3,6},14},{{2,6},19}}

Selected edge	Forest components
{2,3}-5	{{2,3}}
{3,4}-5	{{2,3,4}}
{4,6}-2	{{2,3,4,6}}
{1,3}2	{{1,2,3,4,6}}
{5,6}2	{{1,2,3,4,5,6}}

In[]:=

BoruvkaKruskalTree[EM1,ShowTreeFalse];

{{{2,3},-5},{{3,4},-5},{{4,6},-2},{{1,3},2},{{5,6},2}}

Total Weight-8

{{{2,3},-5},{{3,4},-5},{{4,6},-2},{{2,4},-1},{{1,3},2},{{1,4},2},{{1,6},2},{{5,6},2},{{3,5},3},{{4,5},3},{{1,2},8},{{1,5},9},{{3,6},14},{{2,6},19}}

Selected edge	Forest components
{2,3}-5	{{2,3}}
{3,4}-5	{{2,3,4}}
{4,6}-2	{{2,3,4,6}}
{1,3}2	{{1,2,3,4,6}}
{5,6}2	{{1,2,3,4,5,6}}

In[]:=

BoruvkaKruskalTree[gM1,ShowTreeFalse,TraceFalse];

{{{2,3},-5},{{3,4},-5},{{4,6},-2},{{1,3},2},{{5,6},2}}

Total Weight-8

Example 4

In[]:=

M2=

∞	2	2	3	2	-4	2
2	∞	∞	2	∞	3	1
2	∞	∞	-3	4	1	∞
3	2	-3	∞	1	2	4
2	∞	4	1	∞	2	∞
-4	3	1	2	2	∞	1
2	1	∞	4	∞	1	∞

;

In[]:=

EM2=ToWeightedEdgeList[M2];gM2=ToEdgeWeightedGraph[M2,GraphLayoutNone];EM2

Out[]=

{{{1,2},2},{{1,3},2},{{1,4},3},{{1,5},2},{{1,6},-4},{{1,7},2},{{2,4},2},{{2,6},3},{{2,7},1},{{3,4},-3},{{3,5},4},{{3,6},1},{{4,5},1},{{4,6},2},{{4,7},4},{{5,6},2},{{6,7},1}}

In[]:=

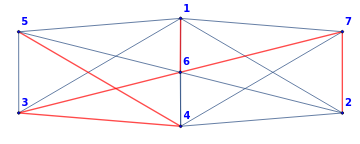
JarnikPrimTree[M2,2,AspectRatio1/3,SelectionRuleLast];

{{{2,7},1},{{7,6},1},{{6,1},-4},{{6,3},1},{{3,4},-3},{{4,5},1}}

Total Weight-3

★

Selected Edge

★

∞

{2,7}1

★

∞

★

{7,6}1

-4

★

{6,1}-4

★

{6,3}1

★

-3

★

{3,4}-3

★

{4,5}1

In[]:=

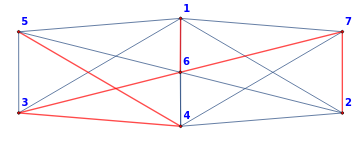
BoruvkaKruskalTree[M2,AspectRatio1/3,SelectionRuleLast];

{{{1,6},-4},{{3,4},-3},{{6,7},1},{{4,5},1},{{3,6},1},{{2,7},1}}

Total Weight-3

{{{1,6},-4},{{3,4},-3},{{2,7},1},{{3,6},1},{{4,5},1},{{6,7},1},{{1,2},2},{{1,3},2},{{1,5},2},{{1,7},2},{{2,4},2},{{4,6},2},{{5,6},2},{{1,4},3},{{2,6},3},{{3,5},4},{{4,7},4}}

Selected edge	Forest components
{1,6}-4	{{1,6}}
{3,4}-3	{{1,6},{3,4}}
{6,7}1	{{1,6,7},{3,4}}
{4,5}1	{{1,6,7},{3,4,5}}
{3,6}1	{{1,3,4,5,6,7}}
{2,7}1	{{1,2,3,4,5,6,7}}

Example 5

In[]:=

M3=

∞	1	-2	4	-1	2	3
1	∞	∞	-2	4	∞	-4
-2	∞	∞	1	3	2	-2
4	-2	1	∞	-3	-2	-1
-1	4	3	-3	∞	1	4
2	∞	2	-2	1	∞	-3
3	-4	-2	-1	4	-3	∞

;

In[]:=

EM3=ToWeightedEdgeList[M3];gM3=ToEdgeWeightedGraph[M3];EM3

Out[]=

{{{1,2},1},{{1,3},-2},{{1,4},4},{{1,5},-1},{{1,6},2},{{1,7},3},{{2,4},-2},{{2,5},4},{{2,7},-4},{{3,4},1},{{3,5},3},{{3,6},2},{{3,7},-2},{{4,5},-3},{{4,6},-2},{{4,7},-1},{{5,6},1},{{5,7},4},{{6,7},-3}}

In[]:=

JarnikPrimTree[EM3,3,SelectionRuleRandomChoice,SortTrue,VertexCoordinatesEllipse[6,2]];

{{{1,3},-2},{{2,4},-2},{{2,7},-4},{{3,7},-2},{{4,5},-3},{{6,7},-3}}

Total Weight-16

★

Selected Edge

-2

∞

★

-2

{3,7}-2

-2

-4

★

-1

-3

★

{2,7}-4

-2

★

-2

-3

★

{6,7}-3

-2

★

-2

★

{2,4}-2

-2

★

-3

★

{4,5}-3

-2

★

{1,3}-2

In[]:=

BoruvkaKruskalTree[EM3,SelectionRuleRandomChoice,SortTrue,TraceTrue,VertexCoordinatesEllipse[6,2]];

{{{1,3},-2},{{2,7},-4},{{3,7},-2},{{4,5},-3},{{4,6},-2},{{6,7},-3}}

Total Weight-16

{{{2,7},-4},{{4,5},-3},{{6,7},-3},{{1,3},-2},{{2,4},-2},{{3,7},-2},{{4,6},-2},{{1,5},-1},{{4,7},-1},{{1,2},1},{{3,4},1},{{5,6},1},{{1,6},2},{{3,6},2},{{1,7},3},{{3,5},3},{{1,4},4},{{2,5},4},{{5,7},4}}

Selected edge	Forest components
{2,7}-4	{{2,7}}
{4,5}-3	{{2,7},{4,5}}
{6,7}-3	{{2,6,7},{4,5}}
{4,6}-2	{{2,4,5,6,7}}
{1,3}-2	{{2,4,5,6,7},{1,3}}
{3,7}-2	{{1,2,3,4,5,6,7}}

Example 6

In[]:=

M4=

∞	-1	∞	-2	4	3	1	∞
-1	∞	∞	∞	4	-1	3	-1
∞	∞	∞	-3	∞	3	2	∞
-2	∞	-3	∞	∞	∞	3	3
4	4	∞	∞	∞	-4	-1	2
3	-1	3	∞	-4	∞	4	4
1	3	2	3	-1	4	∞	-4
∞	-1	∞	3	2	4	-4	∞

;

In[]:=

EM4=ToWeightedEdgeList[M4];gM4=ToEdgeWeightedGraph[M4];EM4

Out[]=

{{{1,2},-1},{{1,4},-2},{{1,5},4},{{1,6},3},{{1,7},1},{{2,5},4},{{2,6},-1},{{2,7},3},{{2,8},-1},{{3,4},-3},{{3,6},3},{{3,7},2},{{4,7},3},{{4,8},3},{{5,6},-4},{{5,7},-1},{{5,8},2},{{6,7},4},{{6,8},4},{{7,8},-4}}

In[]:=

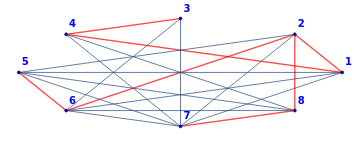
JarnikPrimTree[gM4,4,SelectionRuleRandomChoice,SortTrue,TraceFalse,VertexCoordinatesEllipse[6,2]];

{{{1,2},-1},{{1,4},-2},{{2,6},-1},{{2,8},-1},{{3,4},-3},{{5,6},-4},{{7,8},-4}}

Total Weight-16

In[]:=

BoruvkaKruskalTree[gM4,SelectionRuleRandomChoice,SortTrue,TraceFalse,VertexCoordinatesEllipse[6,2]];

{{{1,2},-1},{{1,4},-2},{{2,6},-1},{{2,8},-1},{{3,4},-3},{{5,6},-4},{{7,8},-4}}

Total Weight-16

Example 7

In[]:=

M5=

∞	∞	-3	3	∞	∞	2	4
∞	∞	2	-3	2	4	∞	3
-3	2	∞	2	-2	-1	4	∞
3	-3	2	∞	∞	∞	∞	3
∞	2	-2	∞	∞	∞	-1	∞
∞	4	-1	∞	∞	∞	3	-2
2	∞	4	∞	-1	3	∞	∞
4	3	∞	3	∞	-2	∞	∞

;

In[]:=

EM5=ToWeightedEdgeList[M5];gM5=ToEdgeWeightedGraph[M5];EM5

Out[]=

{{{1,3},-3},{{1,4},3},{{1,7},2},{{1,8},4},{{2,3},2},{{2,4},-3},{{2,5},2},{{2,6},4},{{2,8},3},{{3,4},2},{{3,5},-2},{{3,6},-1},{{3,7},4},{{4,8},3},{{5,7},-1},{{6,7},3},{{6,8},-2}}

In[]:=

JarnikPrimTree[M5,5,ShowTreeFalse,TraceFalse];

{{{5,3},-2},{{3,1},-3},{{3,6},-1},{{6,8},-2},{{5,7},-1},{{5,2},2},{{2,4},-3}}

Total Weight-10

In[]:=

BoruvkaKruskalTree[EM5,ShowTreeFalse,TraceFalse];

{{{1,3},-3},{{2,4},-3},{{3,5},-2},{{6,8},-2},{{3,6},-1},{{5,7},-1},{{2,3},2}}

Total Weight-10

Example 8

In[]:=

M6=

∞	∞	-2	1	-1	1	∞	-1	1	∞
∞	∞	2	4	∞	∞	∞	∞	∞	-4
-2	2	∞	∞	∞	∞	∞	∞	2	∞
1	4	∞	∞	-3	-3	-2	∞	∞	3
-1	∞	∞	-3	∞	∞	∞	∞	1	∞
1	∞	∞	-3	∞	∞	∞	∞	∞	-4
∞	∞	∞	-2	∞	∞	∞	-3	-4	3
-1	∞	∞	∞	∞	∞	-3	∞	∞	∞
1	∞	2	∞	1	∞	-4	∞	∞	3
∞	-4	∞	3	∞	-4	3	∞	3	∞

;

In[]:=

EM6=ToWeightedEdgeList[M6];gM6=ToEdgeWeightedGraph[M6];EM6

Out[]=

{{{1,3},-2},{{1,4},1},{{1,5},-1},{{1,6},1},{{1,8},-1},{{1,9},1},{{2,3},2},{{2,4},4},{{2,10},-4},{{3,9},2},{{4,5},-3},{{4,6},-3},{{4,7},-2},{{4,10},3},{{5,9},1},{{6,10},-4},{{7,8},-3},{{7,9},-4},{{7,10},3},{{9,10},3}}

In[]:=

JarnikPrimTree[EM6,6,ShowTreeFalse,TraceTrue,TreeFalse];

★

Selected Edge

∞

-3

∞

★

∞

-4

{6,10}-4

-4

∞

-3

∞

★

∞

★

{10,2}-4

★

-3

∞

★

∞

★

{6,4}-3

★

-3

★

-2

∞

★

{4,5}-3

-1

★

-2

∞

★

{4,7}-2

-1

★

-3

-4

★

{7,9}-4

-1

★

-3

★

{7,8}-3

-1

★

{5,1}-1

★

-2

★

{1,3}-2

In[]:=

BoruvkaKruskalTree[EM6,ShowTreeFalse,TraceTrue,TreeFalse];

{{{2,10},-4},{{6,10},-4},{{7,9},-4},{{4,5},-3},{{4,6},-3},{{7,8},-3},{{1,3},-2},{{4,7},-2},{{1,5},-1},{{1,8},-1},{{1,4},1},{{1,6},1},{{1,9},1},{{5,9},1},{{2,3},2},{{3,9},2},{{4,10},3},{{7,10},3},{{9,10},3},{{2,4},4}}

Selected edge	Forest components
{2,10}-4	{{2,10}}
{6,10}-4	{{2,6,10}}
{7,9}-4	{{2,6,10},{7,9}}
{4,5}-3	{{2,6,10},{7,9},{4,5}}
{4,6}-3	{{2,4,5,6,10},{7,9}}
{7,8}-3	{{2,4,5,6,10},{7,8,9}}
{1,3}-2	{{2,4,5,6,10},{7,8,9},{1,3}}
{4,7}-2	{{2,4,5,6,7,8,9,10},{1,3}}
{1,5}-1	{{1,2,3,4,5,6,7,8,9,10}}

Example 9

In[]:=

M7=

∞	3	∞	-2	7	2	∞	9	∞	∞
3	∞	-2	∞	∞	3	8	5	2	∞
∞	-2	∞	∞	∞	4	∞	-2	1	∞
-2	∞	∞	∞	9	1	2	∞	7	3
7	∞	∞	9	∞	∞	-2	∞	∞	-1
2	3	4	1	∞	∞	∞	6	∞	6
∞	8	∞	2	-2	∞	∞	∞	3	∞
9	5	-2	∞	∞	6	∞	∞	1	∞
∞	2	1	7	∞	∞	3	1	∞	9
∞	∞	∞	3	-1	6	∞	∞	9	∞

;

In[]:=

EM7=ToWeightedEdgeList[M7];gM7=ToEdgeWeightedGraph[M7];EM7

Out[]=

{{{1,2},3},{{1,4},-2},{{1,5},7},{{1,6},2},{{1,8},9},{{2,3},-2},{{2,6},3},{{2,7},8},{{2,8},5},{{2,9},2},{{3,6},4},{{3,8},-2},{{3,9},1},{{4,5},9},{{4,6},1},{{4,7},2},{{4,9},7},{{4,10},3},{{5,7},-2},{{5,10},-1},{{6,8},6},{{6,10},6},{{7,9},3},{{8,9},1},{{9,10},9}}

In[]:=

JarnikPrimTree[gM7,7,SelectionRuleRandomChoice,ShowTreeTrue,SortTrue,VertexCoordinatesEllipse[6,3]]

{{{1,4},-2},{{2,3},-2},{{3,8},-2},{{3,9},1},{{4,6},1},{{4,7},2},{{5,7},-2},{{5,10},-1},{{7,9},3}}

Total Weight-2

★

Selected Edge

∞

-2

∞

★

∞

{5,7}-2

∞

★

∞

★

∞

-1

{5,10}-1

∞

★

∞

★

{4,7}2

-2

∞

★

∞

★

{1,4}-2

★

∞

★

{4,6}1

★

{7,9}3

★

{3,9}1

★

-2

★

-2

★

{3,8}-2

★

-2

★

{2,3}-2

In[]:=

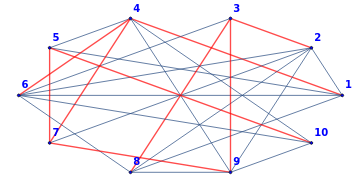
BoruvkaKruskalTree[gM7,SelectionRuleRandomChoice,ShowTreeTrue,SortTrue,VertexCoordinatesEllipse[6,3]];

{{{1,2},3},{{1,4},-2},{{2,3},-2},{{3,8},-2},{{4,6},1},{{4,7},2},{{5,7},-2},{{5,10},-1},{{8,9},1}}

Total Weight-2

{{{1,4},-2},{{2,3},-2},{{3,8},-2},{{5,7},-2},{{5,10},-1},{{3,9},1},{{4,6},1},{{8,9},1},{{1,6},2},{{2,9},2},{{4,7},2},{{1,2},3},{{2,6},3},{{4,10},3},{{7,9},3},{{3,6},4},{{2,8},5},{{6,8},6},{{6,10},6},{{1,5},7},{{4,9},7},{{2,7},8},{{1,8},9},{{4,5},9},{{9,10},9}}

Selected edge	Forest components
{3,8}-2	{{3,8}}
{1,4}-2	{{3,8},{1,4}}
{2,3}-2	{{2,3,8},{1,4}}
{5,7}-2	{{2,3,8},{1,4},{5,7}}
{5,10}-1	{{2,3,8},{1,4},{5,7,10}}
{4,6}1	{{2,3,8},{1,4,6},{5,7,10}}
{8,9}1	{{2,3,8,9},{1,4,6},{5,7,10}}
{4,7}2	{{2,3,8,9},{1,4,5,6,7,10}}
{1,2}3	{{1,2,3,4,5,6,7,8,9,10}}

Strong Components, Condensation and Tarjan’s algorithm

Options

Alternatives for optional arguments of Tarjan (default value = the first alternative): -- FontSize -> 10 | Any font size,-- ItemSize -> Automatic | {2, 2, 3 , 3, 3, 14, 14, 5, 12, 2},-- SelectionRule -> First | Last | RandomChoice,-- Sort  True | False,- Spacings -> { 0.5, {1, {0.5}}} | Automatic,-- Trace  True | Reduced | False,-- TableBreaks  False | integer | list of integers > 1

Alternatives for optional arguments of Condensation: -- AspectRatio -> Automatic | as for Graphics,-- GraphLayout  Automatic | as for Graph, -- ImagePadding  10,-- ImageSize -> Automatic | as for Graphics, -- Tarjan -> False | True,--VertexLabels -> “Name” | as for Graph,-- VertexSize -> Automatic | as for Graph,-- VertexStyle -> Automatic | as for Graph.

In[]:=

Options/@{Tarjan,Condensation}//Column[#,Center,Spacings1]&

Out[]=

{FontSize10,ItemSizeAutomatic,SelectionRuleFirst,SortFalse,Spacings{0.5,{1,{0.5}}},TraceTrue,TableBreaksFalse}

{AspectRatioAutomatic,GraphLayoutAutomatic,ImagePadding10,ImageSizeAutomatic,SortFalse,TarjanTrue,VertexSizeAutomatic,VertexStyleAutomatic}

Example 10

In[]:=

E9={{1,7},{1,10},{2,4},{3,5},{4,6},{5,4},{5,6},{5,7},{5,10},{6,2},{7,10},{8,1},{9,7},{9,8},{10,3}};ME9=ToWeightedAdjacencyMatrix[E9];gE9=ToGraph[E9,DirectedEdgesTrue,GraphLayoutAutomatic,VertexLabels"Name",VertexStyleRed,ImagePadding10]

Out[]=

In[]:=

{ConnectedComponents[gE9],StrongComponents[gE9],StrongComponents[ME9],StrongComponents[E9]}//Column

Out[]=

{{2,4,6},{3,5,7,10},{1},{8},{9}}

{{1},{2,4,6},{3,5,7,10},{8},{9}}

In[]:=

Tarjan[gE9,1,SelectionRuleFirst,TraceFalse]

Out[]=

{{4,6,2},{7,10,3,5},{1},{8},{9}}

In[]:=

Tarjan[gE9,1,ItemSizeAutomatic,SelectionRuleFirst,TraceTrue]

{{4,6,2},{7,10,3,5},{1},{8},{9}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	1	2	1	1	{1,7}	{1,7}	17
2	7	1	2	2	{1,7,10}	{1,7,10}	710
3	10	1	3	3	{1,7,10,3}	{1,7,10,3}	103
4	3	1	4	4	{1,7,10,3,5}	{1,7,10,3,5}	35
5	5	4	5	5	{1,7,10,3,5,4}	{1,7,10,3,5,4}	54
6	4	1	6	6	{1,7,10,3,5,4,6}	{1,7,10,3,5,4,6}	46
7	6	1	7	7	{1,7,10,3,5,4,6,2}	{1,7,10,3,5,4,6,2}	62
8	2	1	8	6	{1,7,10,3,5,4,6,2}	{1,7,10,3,5,4,6,2}	24
8	6	0	7	6	{1,7,10,3,5,4,6}	{1,7,10,3,5,4,6,2}
8	4	0	6	6	{1,7,10,3,5,4}	{1,7,10,3,5,4,6,2}
8	4	0	6	6	{1,7,10,3,5}	{1,7,10,3,5}		{4,6,2}
8	5	2	5	2	{1,7,10,3,5}	{1,7,10,3,5}	57
8	5	1	5	2	{1,7,10,3,5}	{1,7,10,3,5}	510
8	3	0	4	2	{1,7,10,3}	{1,7,10,3,5}
8	10	0	3	2	{1,7,10}	{1,7,10,3,5}
8	7	0	2	2	{1,7}	{1,7,10,3,5}
8	7	0	2	2	{1}	{1}		{7,10,3,5}
8	1	0	1	1	{}	{}		{1}
8	8	0	8	8	{}	{}		{8}
8	9	0	8	8	{}	{}		{9}

In[]:=

Tarjan[E9,1,ItemSizeAutomatic,SelectionRuleLast,TraceTrue]

{{6,2,4},{10,3,5,7},{1},{8},{9}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	1	2	1	1	{1,10}	{1,10}	110
2	10	1	2	2	{1,10,3}	{1,10,3}	103
3	3	1	3	3	{1,10,3,5}	{1,10,3,5}	35
4	5	4	4	2	{1,10,3,5}	{1,10,3,5}	510
4	5	3	4	2	{1,10,3,5,7}	{1,10,3,5,7}	57
5	7	1	5	2	{1,10,3,5,7}	{1,10,3,5,7}	710
5	5	2	4	2	{1,10,3,5}	{1,10,3,5,7}
5	5	2	4	2	{1,10,3,5,6}	{1,10,3,5,7,6}	56
6	6	1	6	6	{1,10,3,5,6,2}	{1,10,3,5,7,6,2}	62
7	2	1	7	7	{1,10,3,5,6,2,4}	{1,10,3,5,7,6,2,4}	24
8	4	1	8	6	{1,10,3,5,6,2,4}	{1,10,3,5,7,6,2,4}	46
8	2	0	7	6	{1,10,3,5,6,2}	{1,10,3,5,7,6,2,4}
8	6	0	6	6	{1,10,3,5,6}	{1,10,3,5,7,6,2,4}
8	6	0	6	6	{1,10,3,5,7}	{1,10,3,5,7}		{6,2,4}
8	5	0	4	2	{1,10,3,5}	{1,10,3,5,7}
8	3	0	3	2	{1,10,3}	{1,10,3,5,7}
8	10	0	2	2	{1,10}	{1,10,3,5,7}
8	10	0	2	2	{1}	{1}		{10,3,5,7}
8	1	0	1	1	{}	{}		{1}
8	9	1	8	8	{9,8}	{9,8}	98
9	8	0	9	9	{9}	{9}		{8}
9	9	0	8	8	{}	{}		{9}

In[]:=

Tarjan[ME9,1,ItemSizeAutomatic,SelectionRuleRandomChoice,TraceTrue]

{{6,2,4},{7,10,3,5},{1},{8},{9}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	1	2	1	1	{1,7}	{1,7}	17
2	7	1	2	2	{1,7,10}	{1,7,10}	710
3	10	1	3	3	{1,7,10,3}	{1,7,10,3}	103
4	3	1	4	4	{1,7,10,3,5}	{1,7,10,3,5}	35
5	5	4	5	5	{1,7,10,3,5,6}	{1,7,10,3,5,6}	56
6	6	1	6	6	{1,7,10,3,5,6,2}	{1,7,10,3,5,6,2}	62
7	2	1	7	7	{1,7,10,3,5,6,2,4}	{1,7,10,3,5,6,2,4}	24
8	4	1	8	6	{1,7,10,3,5,6,2,4}	{1,7,10,3,5,6,2,4}	46
8	2	0	7	6	{1,7,10,3,5,6,2}	{1,7,10,3,5,6,2,4}
8	6	0	6	6	{1,7,10,3,5,6}	{1,7,10,3,5,6,2,4}
8	6	0	6	6	{1,7,10,3,5}	{1,7,10,3,5}		{6,2,4}
8	5	2	5	2	{1,7,10,3,5}	{1,7,10,3,5}	57
8	5	1	5	2	{1,7,10,3,5}	{1,7,10,3,5}	510
8	3	0	4	2	{1,7,10,3}	{1,7,10,3,5}
8	10	0	3	2	{1,7,10}	{1,7,10,3,5}
8	7	0	2	2	{1,7}	{1,7,10,3,5}
8	7	0	2	2	{1}	{1}		{7,10,3,5}
8	1	0	1	1	{}	{}		{1}
8	9	1	8	8	{9,8}	{9,8}	98
9	8	0	9	9	{9}	{9}		{8}
9	9	0	8	8	{}	{}		{9}

In[]:=

Condensation[E9,GraphLayout"SpringEmbedding",ImageSize{300,Automatic},VertexSize0.5Small,VertexStyleRed]

Out[]=

{1{4,6,2},2{7,10,3,5},3{1},4{8},5{9}}

Example 11

In[]:=

E10={12,21,31,48,49,59,52,510,51,610,69,64,74,82,87,98,105,106,104};gE10=ToGraph[E10,GraphLayoutAutomatic,VertexLabels"Name",VertexStyleRed,ImagePadding10]

Out[]=

In[]:=

{ConnectedComponents[gE10],StrongComponents[E10]}//Column

Out[]=

{{1,2},{3},{4,7,8,9},{5,6,10}}

In[]:=

SeedRandom[20!];Tarjan[E10,2,SelectionRuleRandomChoice,SortTrue,TraceReduce]

{{3},{1,2},{5,6,10},{4,7,8,9}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	2	1	1	1	{2,1}	{2,1}	21
2	1	1	2	1	{2,1}	{2,1}	12
2	2	0	1	1	{}	{}		{2,1}
2	8	1	2	2	{8,7}	{8,7}	87
3	7	1	3	3	{8,7,4}	{8,7,4}	74
4	4	2	4	4	{8,7,4,9}	{8,7,4,9}	49
5	9	1	5	2	{8,7,4,9}	{8,7,4,9}	98
5	4	1	4	2	{8,7,4}	{8,7,4,9}	48
5	8	0	2	2	{}	{}		{8,7,4,9}
5	5	1	5	5	{5,10}	{5,10}	510
6	10	2	6	5	{5,10}	{5,10}	105
6	10	1	6	5	{5,10,6}	{5,10,6}	106
7	6	1	7	6	{5,10,6}	{5,10,6}	610
7	5	0	5	5	{}	{}		{5,10,6}
7	3	0	7	7	{}	{}		{3}

In[]:=

SeedRandom[20!];Tarjan[E10,2,SelectionRuleRandomChoice];

{{2,1},{8,7,4,9},{5,10,6},{3}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	2	1	1	1	{2,1}	{2,1}	21
2	1	1	2	1	{2,1}	{2,1}	12
2	2	0	1	1	{2}	{2,1}
2	2	0	1	1	{}	{}		{2,1}
2	8	1	2	2	{8,7}	{8,7}	87
3	7	1	3	3	{8,7,4}	{8,7,4}	74
4	4	2	4	4	{8,7,4,9}	{8,7,4,9}	49
5	9	1	5	2	{8,7,4,9}	{8,7,4,9}	98
5	4	1	4	2	{8,7,4}	{8,7,4,9}
5	4	1	4	2	{8,7,4}	{8,7,4,9}	48
5	7	0	3	2	{8,7}	{8,7,4,9}
5	8	0	2	2	{8}	{8,7,4,9}
5	8	0	2	2	{}	{}		{8,7,4,9}
5	5	1	5	5	{5,10}	{5,10}	510
6	10	2	6	5	{5,10}	{5,10}	105
6	10	1	6	5	{5,10,6}	{5,10,6}	106
7	6	1	7	6	{5,10,6}	{5,10,6}	610
7	10	0	6	5	{5,10}	{5,10,6}
7	5	0	5	5	{5}	{5,10,6}
7	5	0	5	5	{}	{}		{5,10,6}
7	3	0	7	7	{}	{}		{3}

In[]:=

Condensation[E10,AspectRatio1/3,ImageSize{300,Automatic},SortTrue,VertexSizeSmall,VertexStyleRed]

Out[]=

{1{3},2{1,2},3{5,6,10},4{4,7,8,9}}

Example 12

In[]:=

E11={110,16,26,36,410,43,52,59,58,56,68,78,71,82,95,106,107,104};gE11=ToGraph[E11];Graph[E11,VertexLabels"Name",VertexStyleRed,ImagePadding10]

Out[]=

In[]:=

{ConnectedComponents[gE11],StrongComponents[gE11]}//Column

Out[]=

{{2,6,8},{3},{1,4,7,10},{5,9}}

{{1,4,7,10},{2,6,8},{3},{5,9}}

In[]:=

SeedRandom[20!];Tarjan[gE11,6,SelectionRuleRandomChoice]

{{6,8,2},{9,5},{3},{1,10,7,4}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	6	1	1	1	{6,8}	{6,8}	68
2	8	1	2	2	{6,8,2}	{6,8,2}	82
3	2	1	3	1	{6,8,2}	{6,8,2}	26
3	8	0	2	1	{6,8}	{6,8,2}
3	6	0	1	1	{6}	{6,8,2}
3	6	0	1	1	{}	{}		{6,8,2}
3	9	1	3	3	{9,5}	{9,5}	95
4	5	1	4	3	{9,5}	{9,5}	59
4	9	0	3	3	{9}	{9,5}
4	9	0	3	3	{}	{}		{9,5}
4	1	1	4	4	{1,10}	{1,10}	110
5	10	2	5	5	{1,10,7}	{1,10,7}	107
6	7	1	6	4	{1,10,7}	{1,10,7}	71
6	10	1	5	4	{1,10}	{1,10,7}
6	10	1	5	4	{1,10,4}	{1,10,7,4}	104
7	4	2	7	7	{1,10,4,3}	{1,10,7,4,3}	43
8	3	0	8	8	{1,10,7,4}	{1,10,7,4}		{3}
8	4	1	7	5	{1,10,7,4}	{1,10,7,4}	410
8	7	0	6	4	{1,10,7}	{1,10,7,4}
8	10	0	5	4	{1,10}	{1,10,7,4}
8	1	0	4	4	{1}	{1,10,7,4}
8	1	0	4	4	{}	{}		{1,10,7,4}

In[]:=

SeedRandom[20!];Tarjan[gE11,6,SelectionRuleRandomChoice,TraceReduce]

{{6,8,2},{9,5},{3},{1,10,7,4}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	6	1	1	1	{6,8}	{6,8}	68
2	8	1	2	2	{6,8,2}	{6,8,2}	82
3	2	1	3	1	{6,8,2}	{6,8,2}	26
3	6	0	1	1	{}	{}		{6,8,2}
3	9	1	3	3	{9,5}	{9,5}	95
4	5	1	4	3	{9,5}	{9,5}	59
4	9	0	3	3	{}	{}		{9,5}
4	1	1	4	4	{1,10}	{1,10}	110
5	10	2	5	5	{1,10,7}	{1,10,7}	107
6	7	1	6	4	{1,10,7}	{1,10,7}	71
6	10	1	5	4	{1,10,4}	{1,10,7,4}	104
7	4	2	7	7	{1,10,4,3}	{1,10,7,4,3}	43
8	3	0	8	8	{1,10,7,4}	{1,10,7,4}		{3}
8	4	1	7	5	{1,10,7,4}	{1,10,7,4}	410
8	1	0	4	4	{}	{}		{1,10,7,4}

In[]:=

Condensation[gE11,AspectRatio1/3,ImageSize{300,Automatic},VertexSizeSmall,VertexStyleRed,ImagePadding10]

Out[]=

{1{6,8,2},2{3},3{1,10,7,4},4{5,9}}

Example 13

In[]:=

E12={{1,5},{2,4},{3,8},{4,10},{4,7},{5,4},{5,3},{5,1},{6,2},{8,9},{8,2},{8,10},{8,3},{9,3},{9,7},{9,4},{10,6}};gE12=ToGraph[E12];Graph[E12,DirectedEdgesTrue,VertexLabels"Name",VertexStyleRed,ImagePadding10]

Out[]=

In[]:=

{ConnectedComponents[gE12],StrongComponents[gE12]}//Column

Out[]=

{{7},{2,4,6,10},{3,8,9},{1,5}}

{{1,5},{2,4,6,10},{3,8,9},{7}}

In[]:=

Tarjan[gE12,2,SortTrue]

{{7},{1,5},{3,8,9},{2,4,6,10}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	2	1	1	1	{2,4}	{2,4}	24
2	4	2	2	2	{2,4,7}	{2,4,7}	47
3	7	0	3	3	{2,4}	{2,4}		{7}
3	4	1	2	2	{2,4,10}	{2,4,10}	410
4	10	1	4	4	{2,4,10,6}	{2,4,10,6}	106
5	6	1	5	1	{2,4,10,6}	{2,4,10,6}	62
5	10	0	4	1	{2,4,10}	{2,4,10,6}
5	4	0	2	1	{2,4}	{2,4,10,6}
5	2	0	1	1	{2}	{2,4,10,6}
5	2	0	1	1	{}	{}		{2,4,10,6}
5	1	1	5	5	{1,5}	{1,5}	15
6	5	2	6	5	{1,5}	{1,5}	51
6	5	1	6	5	{1,5,3}	{1,5,3}	53
7	3	1	7	7	{1,5,3,8}	{1,5,3,8}	38
8	8	2	8	7	{1,5,3,8}	{1,5,3,8}	83
8	8	1	8	7	{1,5,3,8,9}	{1,5,3,8,9}	89
9	9	1	9	7	{1,5,3,8,9}	{1,5,3,8,9}	93
9	8	0	8	7	{1,5,3,8}	{1,5,3,8,9}
9	3	0	7	7	{1,5,3}	{1,5,3,8,9}
9	3	0	7	7	{1,5}	{1,5}		{3,8,9}
9	1	0	5	5	{1}	{1,5}
9	1	0	5	5	{}	{}		{1,5}

In[]:=

Condensation[gE12,AspectRatio1/3,ImageSize{300,Automatic},VertexSizeSmall,VertexStyleRed]

Out[]=

{1{7},2{4,10,6,2},3{3,8,9},4{1,5}}

Example 14

In[]:=

E13={{1,2},{1,4},{2,5},{2,10},{3,1},{3,6},{3,9},{3,10},{3,11},{4,2},{4,5},{4,6},{4,7},{4,9},{5,1},{5,6},{5,10},{6,9},{7,6},{8,10},{8,12},{9,7},{9,10},{11,4},{11,7},{11,8},{11,9},{12,7},{12,9},{12,10},{12,11}};gE13=ToGraph[E13];Graph[E13,DirectedEdgesTrue,VertexLabels"Name",VertexStyleRed,ImagePadding10]

Out[]=

In[]:=

{ConnectedComponents[gE13],StrongComponents[E13]}//Column

Out[]=

{{10},{6,7,9},{1,2,4,5},{8,11,12},{3}}

{{1,2,4,5},{3},{6,7,9},{8,11,12},{10}}

In[]:=

SeedRandom[20!];Tarjan[gE13,10,SelectionRuleRandomChoice,Trace->Reduce]

{{10},{9,7,6},{5,1,2,4},{12,11,8},{3}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	10	0	1	1	{}	{}		{10}
2	5	2	2	2	{5,1}	{5,1}	51
3	1	2	3	3	{5,1,2}	{5,1,2}	12
4	2	1	4	2	{5,1,2}	{5,1,2}	25
4	1	1	3	2	{5,1,4}	{5,1,2,4}	14
5	4	5	5	5	{5,1,4,9}	{5,1,2,4,9}	49
6	9	1	6	6	{5,1,4,9,7}	{5,1,2,4,9,7}	97
7	7	1	7	7	{5,1,4,9,7,6}	{5,1,2,4,9,7,6}	76
8	6	1	8	6	{5,1,4,9,7,6}	{5,1,2,4,9,7,6}	69
8	9	0	6	6	{5,1,2,4}	{5,1,2,4}		{9,7,6}
8	4	2	5	4	{5,1,2,4}	{5,1,2,4}	42
8	4	1	5	2	{5,1,2,4}	{5,1,2,4}	45
8	5	0	2	2	{}	{}		{5,1,2,4}
8	12	1	8	8	{12,11}	{12,11}	1211
9	11	1	9	9	{12,11,8}	{12,11,8}	118
10	8	1	10	8	{12,11,8}	{12,11,8}	812
10	12	0	8	8	{}	{}		{12,11,8}
10	3	0	10	10	{}	{}		{3}

In[]:=

SeedRandom[20!];Tarjan[gE13,10,SelectionRuleRandomChoice]

{{10},{9,7,6},{5,1,2,4},{12,11,8},{3}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	10	0	1	1	{}	{}		{10}
2	5	2	2	2	{5,1}	{5,1}	51
3	1	2	3	3	{5,1,2}	{5,1,2}	12
4	2	1	4	2	{5,1,2}	{5,1,2}	25
4	1	1	3	2	{5,1}	{5,1,2}
4	1	1	3	2	{5,1,4}	{5,1,2,4}	14
5	4	5	5	5	{5,1,4,9}	{5,1,2,4,9}	49
6	9	1	6	6	{5,1,4,9,7}	{5,1,2,4,9,7}	97
7	7	1	7	7	{5,1,4,9,7,6}	{5,1,2,4,9,7,6}	76
8	6	1	8	6	{5,1,4,9,7,6}	{5,1,2,4,9,7,6}	69
8	7	0	7	6	{5,1,4,9,7}	{5,1,2,4,9,7,6}
8	9	0	6	6	{5,1,4,9}	{5,1,2,4,9,7,6}
8	9	0	6	6	{5,1,2,4}	{5,1,2,4}		{9,7,6}
8	4	2	5	4	{5,1,2,4}	{5,1,2,4}	42
8	4	1	5	2	{5,1,2,4}	{5,1,2,4}	45
8	2	0	4	2	{5,1,2}	{5,1,2,4}
8	1	0	3	2	{5,1}	{5,1,2,4}
8	5	0	2	2	{5}	{5,1,2,4}
8	5	0	2	2	{}	{}		{5,1,2,4}
8	12	1	8	8	{12,11}	{12,11}	1211
9	11	1	9	9	{12,11,8}	{12,11,8}	118
10	8	1	10	8	{12,11,8}	{12,11,8}	812
10	11	0	9	8	{12,11}	{12,11,8}
10	12	0	8	8	{12}	{12,11,8}
10	12	0	8	8	{}	{}		{12,11,8}
10	3	0	10	10	{}	{}		{3}

In[]:=

Condensation[gE13,DirectedEdgesTrue,VertexStyleRed,ImagePadding10]

Out[]=

{1{10},2{6,9,7},3{1,2,5,4},4{11,8,12},5{3}}

Example 15

In[]:=

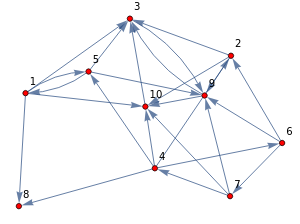
E14={42,39,18,51,13,67,46,62,48,45,410,910,29,59,710,93,210,74,103,53,79,69,23,15,110};gE14=Graph[E14,ImageSize{300,Automatic},VertexLabels->"Name",VertexStyleRed,ImagePadding10]

Out[]=

In[]:=

{ConnectedComponents[gE14],StrongComponents[gE14]}//Column

Out[]=

{{3,9,10},{2},{8},{1,5},{4,6,7}}

{{4,6,7},{1,5},{2},{3,9,10},{8}}

In[]:=

Tarjan[gE14,4,Spacings{1,{1,0.5}},TableBreaks{14}]

{{9,10,3},{2},{8},{5,1},{4,6,7}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	4	5	1	1	{4,2}	{4,2}	42
2	2	3	2	2	{4,2,9}	{4,2,9}	29
3	9	2	3	3	{4,2,9,10}	{4,2,9,10}	910
4	10	1	4	4	{4,2,9,10,3}	{4,2,9,10,3}	103
5	3	1	5	3	{4,2,9,10,3}	{4,2,9,10,3}	39
5	10	0	4	3	{4,2,9,10}	{4,2,9,10,3}
5	9	1	3	3	{4,2,9}	{4,2,9,10,3}
5	9	1	3	3	{4,2,9}	{4,2,9,10,3}	93
5	9	0	3	3	{4,2}	{4,2}		{9,10,3}
5	2	0	2	2	{4}	{4}		{2}
5	4	3	1	1	{4,6}	{4,6}	46
6	6	1	6	6	{4,6,7}	{4,6,7}	67
7	7	1	7	1	{4,6,7}	{4,6,7}	74
7	6	0	6	1	{4,6}	{4,6,7}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
7	4	2	1	1	{4}	{4,6,7}
7	4	2	1	1	{4,8}	{4,6,7,8}	48
8	8	0	8	8	{4,6,7}	{4,6,7}		{8}
8	6	0	6	1	{4,6}	{4,6,7}
8	4	1	1	1	{4}	{4,6,7}
8	4	1	1	1	{4,5}	{4,6,7,5}	45
9	5	1	9	9	{4,5,1}	{4,6,7,5,1}	51
10	1	1	10	9	{4,5,1}	{4,6,7,5,1}	15
10	5	0	9	9	{4,5}	{4,6,7,5,1}
10	5	0	9	9	{4,6,7}	{4,6,7}		{5,1}
10	6	0	6	1	{4,6}	{4,6,7}
10	4	0	1	1	{4}	{4,6,7}
10	4	0	1	1	{}	{}		{4,6,7}

In[]:=

Tarjan[E14,4,SortFalse,Spacings{1,{1,0.5}},TableBreaks{14}]

{{9,10,3},{2},{8},{5,1},{4,6,7}}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
1	4	5	1	1	{4,2}	{4,2}	42
2	2	3	2	2	{4,2,9}	{4,2,9}	29
3	9	2	3	3	{4,2,9,10}	{4,2,9,10}	910
4	10	1	4	4	{4,2,9,10,3}	{4,2,9,10,3}	103
5	3	1	5	3	{4,2,9,10,3}	{4,2,9,10,3}	39
5	10	0	4	3	{4,2,9,10}	{4,2,9,10,3}
5	9	1	3	3	{4,2,9}	{4,2,9,10,3}
5	9	1	3	3	{4,2,9}	{4,2,9,10,3}	93
5	9	0	3	3	{4,2}	{4,2}		{9,10,3}
5	2	0	2	2	{4}	{4}		{2}
5	4	3	1	1	{4,6}	{4,6}	46
6	6	1	6	6	{4,6,7}	{4,6,7}	67
7	7	1	7	1	{4,6,7}	{4,6,7}	74
7	6	0	6	1	{4,6}	{4,6,7}

i	x	+ d (x)	P(x)	Z(x)	ST1	ST2	e	c
7	4	2	1	1	{4}	{4,6,7}
7	4	2	1	1	{4,8}	{4,6,7,8}	48
8	8	0	8	8	{4,6,7}	{4,6,7}		{8}
8	6	0	6	1	{4,6}	{4,6,7}
8	4	1	1	1	{4}	{4,6,7}
8	4	1	1	1	{4,5}	{4,6,7,5}	45
9	5	1	9	9	{4,5,1}	{4,6,7,5,1}	51
10	1	1	10	9	{4,5,1}	{4,6,7,5,1}	15
10	5	0	9	9	{4,5}	{4,6,7,5,1}
10	5	0	9	9	{4,6,7}	{4,6,7}		{5,1}
10	6	0	6	1	{4,6}	{4,6,7}
10	4	0	1	1	{4}	{4,6,7}
10	4	0	1	1	{}	{}		{4,6,7}

In[]:=

Condensation[E14,AspectRatio1/3,DirectedEdgesTrue,ImageSize{300,Automatic},SortTrue,VertexSizeSmall,VertexStyleRed,ImagePadding10]

Out[]=

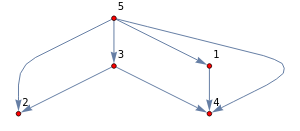{1{2},2{8},3{1,5},4{3,9,10},5{4,6,7}}

Topological Order, TopologicalOrderTest

Options

Alternatives for optional arguments of TopologicalOrder:
-- EdgeList → True | False,
-- FontSize -> 10 | Any font size,
-- Print -> False | True,
-- SelectionRule ->First | Last | RandomChoice,
-- Sort  False | True,
-- Spacings -> {1, 1},
-- TableBreaks -> False | integer | list of integers,
-- Trace -> True | False,
-- Vertices  True | False.

Alternatives for optional arguments of TopologicalOrderTest:
-- Trace -> True | False.

In[]:=

Options[TopologicalOrder]

Out[]=

{EdgeListTrue,FontSize10,Method1,PrintFalse,SelectionRuleFirst,SortFalse,Spacings{0.5,1},TableBreaksFalse,TraceFalse,VertexListTrue}

Example 16

In[]:=

V15=Range[12];E15={14,15,110,111,112,24,210,312,412,58,512,62,63,68,71,72,78,79,710,712,89,114,118,1110,1210};ME15=ToWeightedAdjacencyMatrix[E15];gE15=ToGraph[E15];ToGraph[E15,AspectRatio0.5,DirectedEdgesTrue,GraphLayoutAutomatic,VertexCoordinatesEllipse[2,1,12],VertexLabels"Name",VertexStyleRed,ImagePadding10]

Out[]=

In[]:=

TopologicalOrder[gE15,Method1,EdgeListTrue,Spacings{0.5,1},TraceTrue]

Out[]=

{{6,7},{1,2,3},{5,11},{4,8},{9,12},{10}}

{6{2,3,8},7{1,2,8,9,10,12},1{4,5,10,11,12},2{4,10},3{12},5{8,12},11{4,8,10},4{12},8{9},12{10}}

[x]

{7}

{6,7}

{6}

{1,2,11}

{1}

★

{5,6,7,11}

{7,8}

{1,2,7,11,12}

{1}

{1,3,4,5,7}

[{6,7}]

{6{2,3,8},7{1,2,8,9,10,12}}

[x]

★

{1,2,11}

{1}

★

{5,11}

{8}

{1,2,11,12}

{1}

{1,3,4,5}

[{1,2,3}]

{1{4,5,10,11,12},2{4,10},3{12}}

[x]

★

{11}

★

{5,11}

{8}

{11,12}

★

{4,5}

[{5,11}]

{5{8,12},11{4,8,10}}

[x]

★

{8}

{12}

★

{4}

[{4,8}]

{4{12},8{9}}

[x]

★

{12}

★

[{9,12}]

{12{10}}

[x]

★

In[]:=

TopologicalOrderTest[gE15,#]&/@{%[[1,1]],%[[1,2]]}

Out[]=

{True,True}

In[]:=

TopologicalOrder[gE15,Method2,EdgeListTrue,Spacings{0.5,1},TableBreaks8,TraceTrue]

Out[]=

{6,7,3,1,2,5,11,4,8,12,9,10}

{6{2,3,8},7{1,2,8,9,10,12},3{12},1{4,5,10,11,12},2{4,10},5{8,12},11{4,8,10},4{12},8{9},12{10}}

[x]

{7}

{6,7}

{6}

{1,2,11}

{1}

★

{5,6,7,11}

{7,8}

{1,2,7,11,12}

{1}

{1,3,4,5,7}

[6]

{6{2,3,8}}

[x]

{7}

★

{1,2,11}

{1}

★

{5,7,11}

{7,8}

{1,2,7,11,12}

{1}

{1,3,4,5,7}

[7]

{7{1,2,8,9,10,12}}

[x]

★

{1,2,11}

{1}

★

{5,11}

{8}

{1,2,11,12}

{1}

{1,3,4,5}

[3]

{3{12}}

[x]

★

{1,2,11}

{1}

★

{5,11}

{8}

{1,2,11,12}

{1}

{1,4,5}

[1]

{1{4,5,10,11,12}}

[x]

★

{2,11}

★

{5,11}

{8}

{2,11,12}

★

{4,5}

[2]

{2{4,10}}

[x]

★

{11}

★

{5,11}

{8}

{11,12}

★

{4,5}

[5]

{5{8,12}}

[x]

★

{11}

★

{11}

{8}

{11,12}

★

{4}

[11]

{11{4,8,10}}

[x]

★

{8}

{12}

★

{4}

[4]

{4{12}}

[x]

★

{8}

{12}

★

[8]

{8{9}}

[x]

★

{12}

★

[12]

{12{10}}

[x]

★

[9]

{9{}}

[x]

★

In[]:=

TopologicalOrderTest[gE15,#]&/@{%[[1,1]],%[[1,2]]}

Out[]=

{True,True}

In[]:=

TopologicalOrder[gE15,Method3,EdgeListTrue,TableBreaks{9,16},TraceTrue]

Out[]=

{6,7,3,1,2,5,11,4,8,12,9,10}

{6{2,3,8},7{1,2,8,9,10,12},3{12},1{4,5,10,11,12},2{4,10},5{8,12},11{4,8,10},4{12},8{9},12{10}}

x	1	2	3	4	5	6	7	8	9	10	11	12
d - [x]	1	2	1	3	1	0	0	4	2	5	1	5
E + [6]	{6{2,3,8}}
d - [x]	1	1	0	3	1	0	0	3	2	5	1	5
E + [7]	{7{1,2,8,9,10,12}}
d - [x]	0	0	0	3	1	0	0	2	1	4	1	4
E + [3]	{3{12}}
d - [x]	0	0	0	3	1	0	0	2	1	4	1	3
E + [1]	{1{4,5,10,11,12}}
d - [x]	0	0	0	2	0	0	0	2	1	3	0	2

x	1	2	3	4	5	6	7	8	9	10	11	12
E + [2]	{2{4,10}}
d - [x]	0	0	0	1	0	0	0	2	1	2	0	2
E + [5]	{5{8,12}}
d - [x]	0	0	0	1	0	0	0	1	1	2	0	1
E + [11]	{11{4,8,10}}
d - [x]	0	0	0	0	0	0	0	0	1	1	0	1
E + [4]	{4{12}}

x	1	2	3	4	5	6	7	8	9	10	11	12
d - [x]	0	0	0	0	0	0	0	0	1	1	0	0
E + [8]	{8{9}}
d - [x]	0	0	0	0	0	0	0	0	0	1	0	0
E + [12]	{12{10}}
d - [x]	0	0	0	0	0	0	0	0	0	0	0	0
E + [9]	{9{}}
d - [x]	0	0	0	0	0	0	0	0	0	0	0	0

In[]:=

TopologicalOrderTest[gE15,#]&/@{%[[1,1]],%[[1,2]]}

Out[]=

{True,True}

Example 17

In[]:=

V16=Range[12];E16={12,29,43,411,52,54,56,58,510,511,512,61,63,611,74,711,81,83,86,87,812,101,102,106,109,1011,1012,112,119,122};gE16=Graph[V16,E16,AspectRatio0.5,DirectedEdgesTrue,GraphLayoutAutomatic,VertexCoordinatesEllipse[2,1,12],VertexLabels"Name",VertexStyleRed,ImagePadding10]

Out[]=

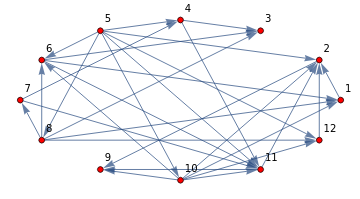
In[]:=

TopologicalOrder[gE16,Method1,TraceTrue]

Out[]=

{{5},{8,10},{6,7,12},{1,4},{3,11},{2},{9}}

{5{2,4,6,8,10,11,12},8{1,3,6,7,12},10{1,2,6,9,11,12},6{1,3,11},7{4,11},12{2},1{2},4{3,11},11{2,9},2{9}}

[x]

{6,8,10}

{1,5,10,11,12}

{4,6,8}

{5,7}

★

{5,8,10}

{8}

{5}

{2,10,11}

{5}

{4,5,6,7,10}

{5,8,10}

[{5}]

{5{2,4,6,8,10,11,12}}

[x]

{6,8,10}

{1,10,11,12}

{4,6,8}

{7}

★

{8,10}

{8}

★

{2,10,11}

★

{4,6,7,10}

{8,10}

[{8,10}]

{8{1,3,6,7,12},10{1,2,6,9,11,12}}

[x]

{6}

{1,11,12}

{4,6}

{7}

★

{2,11}

★

{4,6,7}

★

[{6,7,12}]

{6{1,3,11},7{4,11},12{2}}

[x]

★

{1,11}

{4}

★

{2,11}

★

{4}

★

[{1,4}]

{1{2},4{3,11}}

[x]

★

{11}

★

{2,11}

★

[{3,11}]

{11{2,9}}

[x]

★

{2}

★

[{2}]

{2{9}}

[x]

★

In[]:=

TopologicalOrderTest[E16,#]&/@{%[[1,1]],%[[1,2]]}

Out[]=

{True,True}

Example 18

In[]:=

V17=Range[12];E17={12,17,110,27,31,412,52,58,511,62,64,65,68,87,812,93,94,96,97,98,910,912,107,111,112,114,117,118,1112,127};gE17=Graph[V17,E17,AspectRatio0.5,DirectedEdgesTrue,GraphLayoutAutomatic,VertexCoordinatesEllipse[2,1,12],VertexLabels"Name",VertexStyleRed,ImagePadding10]

Out[]=

In[]:=

TopologicalOrder[gE17,Method2,Spacings{0.3,1},TraceTrue]

Out[]=

{9,3,6,5,11,1,4,2,8,10,12,7}

{9{3,4,6,7,8,10,12},3{1},6{2,4,5,8},5{2,8,11},11{1,2,4,7,8,12},1{2,7,10},4{12},2{7},8{7,12},10{7},12{7}}

[x]

{3,11}

{1,5,6,11}

{9}

{6,9,11}

{6}

{9}

{1,2,8,9,10,11,12}

{5,6,9,11}

★

{1,9}

{5}

{4,8,9,11}

[9]

{9{3,4,6,7,8,10,12}}

[x]

{3,11}

{1,5,6,11}

★

{6,11}

{6}

★

{1,2,8,10,11,12}

{5,6,11}

★

{1}

{5}

{4,8,11}

[3]

{3{1}}

[x]

{11}

{1,5,6,11}

★

{6,11}

{6}

★

{1,2,8,10,11,12}

{5,6,11}

★

{1}

{5}

{4,8,11}

[6]

{6{2,4,5,8}}

[x]

{11}

{1,5,11}

★

{11}

★

{1,2,8,10,11,12}

{5,11}

★

{1}

{5}

{4,8,11}

[5]

{5{2,8,11}}

[x]

{11}

{1,11}

★

{11}

★

{1,2,8,10,11,12}

{11}

★

{1}

★

{4,8,11}

[11]

{11{1,2,4,7,8,12}}

[x]

★

{1}

★

{1,2,8,10,12}

★

{1}

★

{4,8}

[1]

{1{2,7,10}}

[x]

★

{2,8,10,12}

★

{4,8}

[4]

{4{12}}

[x]

★

{2,8,10,12}

★

{8}

[2]

{2{7}}

[x]

★

{8,10,12}

★

{8}

[8]

{8{7,12}}

[x]

★

{10,12}

★

[10]

{10{7}}

[x]

★

{12}

★

[12]

{12{7}}

[x]

★

In[]:=

TopologicalOrderTest[gE17,#]&/@{%[[1,1]],%[[1,2]]}

Out[]=

{True,True}

Example 19

In[]:=

V18=Range[12];E18={15,110,23,24,26,210,212,53,65,610,72,75,76,81,83,87,94,103,104,111,112,115,116,117,118,119,1110,123,124,125};gE18=Graph[V18,E18,AspectRatio0.5,DirectedEdgesTrue,GraphLayoutAutomatic,VertexCoordinatesEllipse[2,1,12],VertexLabels"Name",VertexStyleRed,ImagePadding10]

Out[]=

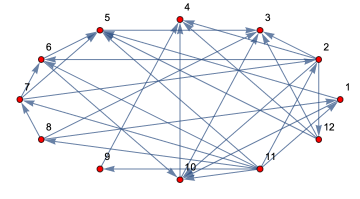
In[]:=

TopologicalOrder[gE18]

Out[]=

{{11},{8,9},{1,7},{2},{6,12},{5,10},{3,4}}

{11{1,2,5,6,7,8,9,10},8{1,3,7},9{4},1{5,10},7{2,5,6},2{3,4,6,10,12},6{5,10},12{3,4,5},5{3},10{3,4}}

In[]:=

TopologicalOrderTest[gE18,#]&/@{%[[1,1]],%[[1,2]]}

Out[]=

{True,True}

Example 20

In[]:=

V19=Range[13];E19={13,111,29,43,412,413,52,53,59,510,511,62,64,610,76,78,82,813,102,103,118,119,1110,129,139};gE19=Graph[V19,E19,AspectRatio0.5,DirectedEdgesTrue,GraphLayoutAutomatic,VertexCoordinatesEllipse[2,1,13],VertexLabels"Name",VertexStyleRed,ImagePadding10]

Out[]=

In[]:=

TopologicalOrder[gE19]

Out[]=

{{1,5,7},{6,11},{4,8,10},{2,3,12,13},{9}}

{1{3,11},5{2,3,9,10,11},7{6,8},6{2,4,10},11{8,9,10},4{3,12,13},8{2,13},10{2,3},2{9},12{9},13{9}}

In[]:=

TopologicalOrderTest[gE19,#]&/@{%[[1,1]],%[[1,2]]}

Out[]=

{True,True}

Example 21

In[]:=

V20=Range[12];E20={{{1,2},2},{{1,6},12},{{5,2},17},{{2,3},1},{{2,8},1},{{3,1},4},{{4,3},3},{{4,6},4},{{4,8},12},{{5,1},8},{{5,4},10},{{6,2},12},{{6,3},12},{{6,7},10},{{8,7},7},{{9,6},4},{{9,10},1},{{10,11},0},{{11,12},-1},{{12,1},3}};gE20=Graph[V20,First/@E20,AspectRatio0.5,DirectedEdgesTrue,GraphLayoutAutomatic,VertexCoordinatesEllipse[2,1,12],VertexLabels"Name",VertexStyleRed,ImagePadding10]

Out[]=

In[]:=

TopologicalOrder[gE20];

Topological order doesn't exist.

Graph isn't acyclic, it contains the folloving cycles:

{{1,2},{2,3},{3,1}}

{{1,6},{6,2},{2,3},{3,1}}

Shortest Paths: DijkstraPathsTree

Options

Alternatives for optional arguments :-- “ArrowSize” -> Automatic | 0.04 | as for Graph,-- DistanceTable → True | False,-- FontSize -> 10 | as for Grid,-- GraphLayout -> Automatic | any Graph layout, -- ImageSize -> Automatic | {450, 300} | as for Graph,-- ItemSize → Automatic | {6,4,2,3,3,5,8,2} | as for Grid,-- SelectionRule → First | Last | RandomChoice, -- ShowTree -> Tree | False,-- Sort →True | False,-- Spacings -> {1,1} | Automatic | as for Grid, -- TableBreaks → False | integer | list of positive integers,-- Trace -> All | Reduce | False,-- Tree -> True | False,-- TreeEdgeStyle → {Thickness[0.005], Red} | as for EdgeStyle,-- VertexCoordinates  Automatic | Ellipse[a, b],-- VertexLabelStyle  Directive[Bold, Blue, 12] | as for Graph,-- VertexSize -> Automatic | Tiny | Small | Medium | Large | number | {“Scaled”, number},-- VertexStyle  Blue | any color specification.

In[]:=

Options[DijkstraPathsTree]

Out[]=

ArrowSizeAutomatic,DijkstraFalse,DistanceTableTrue,FontSize10,GraphLayoutAutomatic,ImagePadding10,ImageSizeAutomatic,ItemSizeAutomatic,SelectionRuleFirst,ShowTreeTrue,Spacings{0.7,0.7},SortTrue,TableBreaksFalse,TraceTrue,TreeTrue,TreeEdgeStyleThickness[0.003],

,VertexCoordinatesAutomatic,VertexLabelsName,VertexSizeAutomatic,VertexStyle

,VertexLabelStyleDirectiveBold,

,12

Example 22

In[]:=

E13={{{1,2},2},{{1,6},12},{{5,2},17},{{2,3},1},{{2,8},1},{{3,1},-4},{{9,6},4},{{4,3},3},{{4,6},4},{{4,8},12},{{5,1},8},{{5,4},10},{{6,2},12},{{6,3},12},{{6,7},10},{{8,7},7}};ME13=ToWeightedAdjacencyMatrix[E13];gE13=ToEdgeWeightedGraph[E13];ME13//MatrixForm

Out[]//MatrixForm=

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	1	∞
-4	∞	0	∞	∞	∞	∞	∞	∞
∞	∞	3	0	∞	4	∞	12	∞
8	17	∞	10	0	∞	∞	∞	∞
∞	12	12	∞	∞	0	10	∞	∞
∞	∞	∞	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	4	∞	∞	0

In[]:=

Transpose@Prepend[Sort[Flatten/@E13],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	2	2	3	4	4	4	5	5	5	6	6	6	8	9
y	2	6	3	8	1	3	6	8	1	2	4	2	3	7	7	6
w	2	12	1	1	-4	3	4	12	8	17	10	12	12	10	7	4

In[]:=

DijkstraPathsTree[gE13,6,VertexCoordinatesEllipse[6,3],VertexSizeSmall]

Found cycle of negative totalWeight

{{31,-4},{12,2},{23,1}}

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{6}	62	12	0	∞	12	62	2
{6,2}	63	12	0	∞	12	63	3
{6,2,3}	67	10	0	∞	10	67	7
{2,3,7}	23	1	12	12	13
{2,3,7}	28	1	12	∞	13	28	8
{3,7,8}	31	-4	12	∞	8	31	1
{8,1}	87	7	13	10	20
{1}	12	2	8	12	10	12	2
{1,2}	16	12	8	0	20
{2}	23	1	10	12	11	23	3

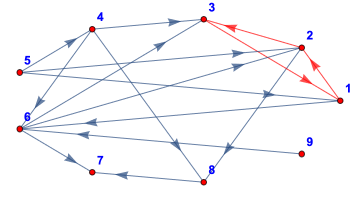
Example 23

In[]:=

E14={{{1,2},2},{{1,6},12},{{5,2},10},{{2,3},1},{{8,2},1},{{4,3},-3},{{4,6},4},{{4,8},2},{{5,1},10},{{5,4},10},{{6,9},-5},{{6,2},12},{{3,9},5},{{6,7},10},{{7,9},1},{{8,7},7},{{9,8},-7}};ME14=ToWeightedAdjacencyMatrix[E14];gE14=ToEdgeWeightedGraph[E14];ME14//MatrixForm

Out[]//MatrixForm=

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	∞	∞
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	∞
10	10	∞	10	0	∞	∞	∞	∞
∞	12	∞	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	∞	∞	-7	0

In[]:=

gE14//EdgeList

Out[]=

{12,16,52,23,82,43,46,48,51,54,69,62,39,67,79,87,98}

In[]:=

Transpose@Prepend[Sort[Flatten/@E14],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	2	3	4	4	4	5	5	5	6	6	6	7	8	8	9
y	2	6	3	9	3	6	8	1	2	4	2	7	9	9	2	7	8
w	2	12	1	5	-3	4	2	10	10	10	12	10	-5	1	1	7	-7

In[]:=

DijkstraPathsTree[ME14,5,SelectionRuleFirst,VertexCoordinatesEllipse[6,3],TableBreaks->{5}]

Vertex	5	1	2	3	4	6	7	8	9
Distance	0	10	3	4	10	14	9	2	9
From Vertex	--	5	8	2	5	4	8	9	6

{{23,1},{46,4},{51,10},{54,10},{69,-5},{82,1},{87,7},{98,-7}}

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{5}	51	10	0	∞	10	51	1
{5,1}	52	10	0	∞	10	52	2
{5,1,2}	54	10	0	∞	10	54	4
{1,2,4}	12	2	10	10	12
{1,2,4}	16	12	10	∞	22	16	6

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{2,4,6}	23	1	10	∞	11	23	3
{4,6,3}	43	-3	10	11	7	43	3
{4,6,3}	46	4	10	22	14	46	6
{4,6,3}	48	2	10	∞	12	48	8
{6,3,8}	62	12	14	10	26
{6,3,8}	67	10	14	∞	24	67	7
{6,3,8,7}	69	-5	14	∞	9	69	9
{3,8,7,9}	39	5	7	9	12
{8,7,9}	82	1	12	10	13
{8,7,9}	87	7	12	24	19	87	7
{7,9}	79	1	19	9	20
{9}	98	-7	9	12	2	98	8
{8}	82	1	2	10	3	82	2
{8,2}	87	7	2	19	9	87	7
{2,7}	23	1	3	7	4	23	3
{7,3}	79	1	9	9	10
{3}	39	5	4	9	9

Example 24

In[]:=

E15={{15,6},{19,4},{16,5},{29,4},{37,2},{36,8},{32,5},{35,5},{46,2},{42,5},{56,4},{76,2},{81,1},{85,4},{87,7},{94,1},{93,2}};ME15=ToWeightedAdjacencyMatrix[E15];gE15=ToEdgeWeightedGraph[E15];ME15//MatrixForm

Out[]//MatrixForm=

0	∞	∞	∞	6	5	∞	∞	4
∞	0	∞	∞	∞	∞	∞	∞	4
∞	5	0	∞	5	8	2	∞	∞
∞	5	∞	0	∞	2	∞	∞	∞
∞	∞	∞	∞	0	4	∞	∞	∞
∞	∞	∞	∞	∞	0	∞	∞	∞
∞	∞	∞	∞	∞	2	0	∞	∞
1	∞	∞	∞	4	∞	7	0	∞
∞	∞	2	1	∞	∞	∞	∞	0

In[]:=

Transpose@Prepend[Sort[Map[Flatten,E15/.EdgeToPair]],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	1	2	3	3	3	3	4	4	5	7	8	8	8	9	9
y	5	6	9	9	2	5	6	7	2	6	6	6	1	5	7	3	4
w	6	5	4	4	5	5	8	2	5	2	4	2	1	4	7	2	1

In[]:=

DijkstraPathsTree[gE15,8,TraceFalse,VertexCoordinatesEllipse[6,3]];

Vertex	8	1	2	3	4	5	6	7	9
Distance	0	1	11	7	6	4	6	7	5
From Vertex	--	8	4	9	9	8	1	8	1

{{16,5},{19,4},{42,5},{81,1},{85,4},{87,7},{93,2},{94,1}}

In[]:=

DijkstraPathsTree[gE15,8,DistanceTableFalse,TraceTrue];

{{16,5},{19,4},{42,5},{81,1},{85,4},{87,7},{93,2},{94,1}}

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{8}	81	1	0	∞	1	81	1
{8,1}	85	4	0	∞	4	85	5
{8,1,5}	87	7	0	∞	7	87	7
{1,5,7}	15	6	1	4	7
{1,5,7}	19	4	1	∞	5	19	9
{1,5,7,9}	16	5	1	∞	6	16	6
{5,7,9,6}	56	4	4	6	8
{7,9,6}	76	2	7	6	9
{9,6}	94	1	5	∞	6	94	4
{9,6,4}	93	2	5	∞	7	93	3
{4,3}	46	2	6	6	8
{4,3}	42	5	6	∞	11	42	2
{3,2}	37	2	7	7	9
{3,2}	36	8	7	6	15
{3,2}	32	5	7	11	12
{3,2}	35	5	7	4	12
{2}	29	4	11	5	15

Example 25

In[]:=

E16={{18,4},{16,5},{14,3},{24,2},{38,7},{36,7},{45,4},{47,4},{58,2},{62,1},{65,3},{63,1},{74,5},{81,5},{82,1}};ME16=ToWeightedAdjacencyMatrix[E16];gE16=ToEdgeWeightedGraph[E16];ME16//MatrixForm

Out[]//MatrixForm=

0	∞	∞	3	∞	5	∞	4
∞	0	∞	2	∞	∞	∞	∞
∞	∞	0	∞	∞	7	∞	7
∞	∞	∞	0	4	∞	4	∞
∞	∞	∞	∞	0	∞	∞	2
∞	1	1	∞	3	0	∞	∞
∞	∞	∞	5	∞	∞	0	∞
5	1	∞	∞	∞	∞	∞	0

In[]:=

Transpose@Prepend[Sort[Map[Flatten,E16/.EdgeToPair]],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	1	2	3	3	4	4	5	6	6	6	7	8	8
y	4	6	8	4	6	8	5	7	8	2	3	5	4	1	2
w	3	5	4	2	7	7	4	4	2	1	1	3	5	5	1

In[]:=

DijkstraPathsTree[E16,5,ImageSize{400,150},Spacings{0.5,1},TableBreaks{10},TraceTrue]

Vertex	5	1	2	3	4	6	7	8
Distance	0	7	3	13	5	12	9	2
From Vertex	--	8	8	6	2	1	4	5

{{16,5},{24,2},{47,4},{58,2},{63,1},{81,5},{82,1}}

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{5}	58	2	0	∞	2	58	8
{8}	81	5	2	∞	7	81	1
{8,1}	82	1	2	∞	3	82	2
{1,2}	18	4	7	2	11
{1,2}	16	5	7	∞	12	16	6
{1,2,6}	14	3	7	∞	10	14	4
{2,6,4}	24	2	3	10	5	24	4
{6,4}	62	1	12	3	13
{6,4}	65	3	12	0	15
{6,4}	63	1	12	∞	13	63	3

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{4,3}	45	4	5	0	9
{4,3}	47	4	5	∞	9	47	7
{3,7}	38	7	13	2	20
{3,7}	36	7	13	12	20
{7}	74	5	9	5	14

In[]:=

DijkstraPathsTree[ME16,5,ImageSize{450,150},ShowTreeTrue,TraceReduce];

Vertex	5	1	2	3	4	6	7	8
Distance	0	7	3	13	5	12	9	2
From Vertex	--	8	8	6	2	1	4	5

{{16,5},{24,2},{47,4},{58,2},{63,1},{81,5},{82,1}}

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{5}	58	2	0	∞	2	58	8
{8}	81	5	2	∞	7	81	1
{8,1}	82	1	2	∞	3	82	2
{1,2}	14	3	7	∞	10	14	4
{1,2,4}	16	5	7	∞	12	16	6
{2,4,6}	24	2	3	10	5	24	4
{4,6}	47	4	5	∞	9	47	7
{6,7}	63	1	12	∞	13	63	3

Example 26

In[]:=

E17={{15,0},{16,4},{17,7},{19,5},{23,7},{28,5},{31,7},{32,6},{35,2},{36,3},{39,4},{46,5},{47,3},{53,4},{58,1},{59,1},{64,7},{69,7},{73,6},{92,5},{95,6},{97,6},{98,5}};ME17=ToWeightedAdjacencyMatrix[E17];gE17=ToEdgeWeightedGraph[E17,DirectedEdgesTrue];ME17//MatrixForm

Out[]//MatrixForm=

0	∞	∞	∞	0	4	7	∞	5
∞	0	7	∞	∞	∞	∞	5	∞
7	6	0	∞	2	3	∞	∞	4
∞	∞	∞	0	∞	5	3	∞	∞
∞	∞	4	∞	0	∞	∞	1	1
∞	∞	∞	7	∞	0	∞	∞	7
∞	∞	6	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	∞	0	∞
∞	5	∞	∞	6	∞	6	5	0

In[]:=

Transpose@Prepend[Sort[Map[Flatten,E17/.EdgeToPair]],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	1	1	2	2	3	3	3	3	3	4	4	5	5	5	6	6	7	9	9	9	9
y	5	6	7	9	3	8	1	2	5	6	9	6	7	3	8	9	4	9	3	2	5	7	8
w	0	4	7	5	7	5	7	6	2	3	4	5	3	4	1	1	7	7	6	5	6	6	5

In[]:=

DijkstraPathsTree[gE17,5,ShowTreeFalse,Spacings{0.5,1},TableBreaks8];

Vertex	5	1	2	3	4	6	7	8	9
Distance	0	11	6	4	14	7	7	1	1
From Vertex	--	3	9	5	6	3	9	5	5

{{31,7},{36,3},{53,4},{58,1},{59,1},{64,7},{92,5},{97,6}}

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{5}	53	4	0	∞	4	53	3
{5,3}	58	1	0	∞	1	58	8
{5,3,8}	59	1	0	∞	1	59	9
{3,8,9}	31	7	4	∞	11	31	1
{3,8,9,1}	32	6	4	∞	10	32	2
{3,8,9,1,2}	35	2	4	0	6
{3,8,9,1,2}	36	3	4	∞	7	36	6
{3,8,9,1,2,6}	39	4	4	1	8

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{9,1,2,6}	92	5	1	10	6	92	2
{9,1,2,6}	95	6	1	0	7
{9,1,2,6}	97	6	1	∞	7	97	7
{9,1,2,6,7}	98	5	1	1	6
{1,2,6,7}	15	0	11	0	11
{1,2,6,7}	16	4	11	7	15
{1,2,6,7}	17	7	11	7	18
{1,2,6,7}	19	5	11	1	16

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{2,6,7}	23	7	6	4	13
{2,6,7}	28	5	6	1	11
{6,7}	64	7	7	∞	14	64	4
{6,7,4}	69	7	7	1	14
{7,4}	73	6	7	4	13
{4}	46	5	14	7	19
{4}	47	3	14	7	17

In[]:=

DijkstraPathsTree[E17,5,DistanceTableFalse,Spacings{0.5,1},ShowTreeFalse,TraceReduce]

{{31,7},{36,3},{53,4},{58,1},{59,1},{64,7},{92,5},{97,6}}

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{5}	53	4	0	∞	4	53	3
{5,3}	58	1	0	∞	1	58	8
{5,3,8}	59	1	0	∞	1	59	9
{3,8,9}	31	7	4	∞	11	31	1
{3,8,9,1}	32	6	4	∞	10	32	2
{3,8,9,1,2}	36	3	4	∞	7	36	6
{9,1,2,6}	92	5	1	10	6	92	2
{9,1,2,6}	97	6	1	∞	7	97	7
{6,7}	64	7	7	∞	14	64	4

Example 27

In[]:=

E18={{13,5},{24,5},{27,1},{28,3},{29,0},{35,3},{36,5},{46,1},{47,4},{56,4},{57,3},{58,2},{59,4},{64,2},{67,0},{69,5},{71,4},{73,5},{74,7},{85,3},{91,6},{92,3},{94,5},{95,6},{98,1}};ME18=ToWeightedAdjacencyMatrix[E18];gE18=ToEdgeWeightedGraph[E18,DirectedEdgesTrue];ME18//MatrixForm

Out[]//MatrixForm=

0	∞	5	∞	∞	∞	∞	∞	∞
∞	0	∞	5	∞	∞	1	3	0
∞	∞	0	∞	3	5	∞	∞	∞
∞	∞	∞	0	∞	1	4	∞	∞
∞	∞	∞	∞	0	4	3	2	4
∞	∞	∞	2	∞	0	0	∞	5
4	∞	5	7	∞	∞	0	∞	∞
∞	∞	∞	∞	3	∞	∞	0	∞
6	3	∞	5	6	∞	∞	1	0

In[]:=

Transpose@Prepend[Sort[Map[Flatten,E18/.EdgeToPair]],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	2	2	2	2	3	3	4	4	5	5	5	5	6	6	6	7	7	7	8	9	9	9	9	9
y	3	4	7	8	9	5	6	6	7	6	7	8	9	4	7	9	1	3	4	5	1	2	4	5	8
w	5	5	1	3	0	3	5	1	4	4	3	2	4	2	0	5	4	5	7	3	6	3	5	6	1

In[]:=

DijkstraPathsTree[E18,5,TraceReduce];

Vertex	5	1	2	3	4	6	7	8	9
Distance	0	7	7	8	6	4	3	2	4
From Vertex	--	7	9	7	6	5	5	5	5

{{56,4},{57,3},{58,2},{59,4},{64,2},{71,4},{73,5},{92,3}}

M	x→y	w	U(x)	U(y)	U(x)+w	FromWhere	y
{5}	56	4	0	∞	4	56	6
{5,6}	57	3	0	∞	3	57	7
{5,6,7}	58	2	0	∞	2	58	8
{5,6,7,8}	59	4	0	∞	4	59	9
{6,7,8,9}	64	2	4	∞	6	64	4
{7,8,9,4}	71	4	3	∞	7	71	1
{7,8,9,4,1}	73	5	3	∞	8	73	3
{9,4,1,3}	92	3	4	∞	7	92	2

In[]:=

DijkstraPathsTree[gE18,6,TraceFalse,TreeFalse]

Vertex	6	1	2	3	4	5	7	8	9
Distance	0	4	8	5	2	8	0	6	5
From Vertex	--	7	9	7	6	3	6	9	6

Shortest Paths: Floyd’s Algorithm

Options

In[]:=

Options[Floyd]

Out[]=

{DistanceTableTrue,FontSize10,FromWhereTableTrue,PartitionFalse,TraceFalse}

Example 22

In[]:=

E19={{{1,2},2},{{1,6},12},{{5,2},17},{{2,3},1},{{2,8},1},{{3,1},-4},{{9,6},4},{{4,3},3},{{4,6},4},{{4,8},12},{{5,1},8},{{5,4},10},{{6,2},12},{{6,3},12},{{6,7},10},{{8,7},7}};ME19=ToWeightedAdjacencyMatrix[E19];gE19=ToEdgeWeightedGraph[E19];ME19//MatrixForm

Out[]//MatrixForm=

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	1	∞
-4	∞	0	∞	∞	∞	∞	∞	∞
∞	∞	3	0	∞	4	∞	12	∞
8	17	∞	10	0	∞	∞	∞	∞
∞	12	12	∞	∞	0	10	∞	∞
∞	∞	∞	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	4	∞	∞	0

In[]:=

Transpose@Prepend[Sort[Flatten/@E19],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	2	2	3	4	4	4	5	5	5	6	6	6	8	9
y	2	6	3	8	1	3	6	8	1	2	4	2	3	7	7	6
w	2	12	1	1	-4	3	4	12	8	17	10	12	12	10	7	4

In[]:=

ToGraph[E19,GraphLayoutAutomatic,ImagePadding10,VertexCoordinates{{0.9191450300180578`,1.0504514628777804`},{1.0504514628777804`,0.5252257314388902`},{0.`,0.5252257314388902`},{0.`,0.`},{0.5252257314388902`,0.5252257314388902`-(1/5)},{1.8382900600361156`,0.5252257314388902`},{2.1009029257555607`,0.`},{1.0504514628777804`,0.`},{1.5756771943166705`,0.`}},VertexLabels"Name",VertexStyleRed]

Out[]=

In[]:=

Floyd[E19]

Out[]=

Found cycle of negative weight

{{31,-4},{12,2},{23,1}}

In[]:=

Floyd[ME19,TraceTrue]

Found cycle of negative weight

{{31,-4},{12,2},{23,1}}

Out[]=



0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	1	∞
-4	∞	0	∞	∞	∞	∞	∞	∞
∞	∞	3	0	∞	4	∞	12	∞
8	17	∞	10	0	∞	∞	∞	∞
∞	12	12	∞	∞	0	10	∞	∞
∞	∞	∞	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	4	∞	∞	0

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	1	∞
-4	-2	0	∞	∞	8	∞	∞	∞
∞	∞	3	0	∞	4	∞	12	∞
8	10	∞	10	0	20	∞	∞	∞
∞	12	12	∞	∞	0	10	∞	∞
∞	∞	∞	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	4	∞	∞	0

0	2	3	∞	∞	12	∞	3	∞
∞	0	1	∞	∞	∞	∞	1	∞
-4	-2	-1	∞	∞	8	∞	-1	∞
∞	∞	3	0	∞	4	∞	12	∞
8	10	11	10	0	20	∞	11	∞
∞	12	12	∞	∞	0	10	13	∞
∞	∞	∞	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	4	∞	∞	0



Example 23

In[]:=

E20={{{1,2},2},{{1,6},12},{{5,2},10},{{2,3},1},{{8,2},1},{{4,3},-3},{{4,6},4},{{4,8},2},{{5,1},10},{{5,4},10},{{6,9},-5},{{6,2},12},{{3,9},5},{{6,7},10},{{7,9},1},{{8,7},7},{{9,8},-7}};ME20=ToWeightedAdjacencyMatrix[E20];gE20=ToEdgeWeightedGraph[E20];ME20//MatrixForm

Out[]//MatrixForm=

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	∞	∞
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	∞
10	10	∞	10	0	∞	∞	∞	∞
∞	12	∞	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	∞	∞	-7	0

In[]:=

Transpose@Prepend[Sort[Flatten/@E20],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	2	3	4	4	4	5	5	5	6	6	6	7	8	8	9
y	2	6	3	9	3	6	8	1	2	4	2	7	9	9	2	7	8
w	2	12	1	5	-3	4	2	10	10	10	12	10	-5	1	1	7	-7

In[]:=

Graph[EdgeList[gE20],ImagePadding10,VertexLabels"Name"]

Out[]=

In[]:=

Floyd[ME20,Partition2,TraceTrue]//Row[#,", "]&/@#&//StylePrint/@#&;

★	1	2	3	4	5	6	7	8	9
1	0	1	2	∞	∞	12	7	0	7
2	∞	0	1	∞	∞	∞	6	-1	6
3	∞	-1	0	∞	∞	∞	5	-2	5
4	∞	-7	-6	0	∞	4	-1	-8	-1
5	10	3	4	10	0	14	9	2	9
6	∞	-11	-10	∞	∞	0	-5	-12	-5
7	∞	-5	-4	∞	∞	∞	0	-6	1
8	∞	1	2	∞	∞	∞	7	0	7
9	∞	-6	-5	∞	∞	∞	0	-7	0

★	1	2	3	4	5	6	7	8	9
1	★	82	23	★	★	16	87	98	69
2	★	★	23	★	★	★	87	98	39
3	★	82	★	★	★	★	87	98	39
4	★	82	23	★	★	46	87	98	69
5	51	82	23	54	★	46	87	98	69
6	★	82	23	★	★	★	87	98	69
7	★	82	23	★	★	★	★	98	79
8	★	82	23	★	★	★	87	★	39
9	★	82	23	★	★	★	87	98	★

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	∞	∞
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	∞
10	10	∞	10	0	∞	∞	∞	∞
∞	12	∞	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	∞	∞	-7	0

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	∞	∞
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	∞
10	10	∞	10	0	22	∞	∞	∞
∞	12	∞	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	∞	∞	-7	0

0	2	3	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	∞	∞
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	∞
10	10	11	10	0	22	∞	∞	∞
∞	12	13	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	2	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	∞	∞	-7	0

0	2	3	∞	∞	12	∞	∞	8
∞	0	1	∞	∞	∞	∞	∞	6
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	2
10	10	11	10	0	22	∞	∞	16
∞	12	13	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	2	∞	∞	∞	7	0	7
∞	∞	∞	∞	∞	∞	∞	-7	0

0	2	3	∞	∞	12	∞	∞	8
∞	0	1	∞	∞	∞	∞	∞	6
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	2
10	10	7	10	0	14	∞	12	12
∞	12	13	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	2	∞	∞	∞	7	0	7
∞	∞	∞	∞	∞	∞	∞	-7	0

0	2	3	∞	∞	12	∞	∞	8
∞	0	1	∞	∞	∞	∞	∞	6
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	2
10	10	7	10	0	14	∞	12	12
∞	12	13	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	2	∞	∞	∞	7	0	7
∞	∞	∞	∞	∞	∞	∞	-7	0

0	2	3	∞	∞	12	22	∞	7
∞	0	1	∞	∞	∞	∞	∞	6
∞	∞	0	∞	∞	∞	∞	∞	5
∞	16	-3	0	∞	4	14	2	-1
10	10	7	10	0	14	24	12	9
∞	12	13	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	2	∞	∞	∞	7	0	7
∞	∞	∞	∞	∞	∞	∞	-7	0

0	2	3	∞	∞	12	22	∞	7
∞	0	1	∞	∞	∞	∞	∞	6
∞	∞	0	∞	∞	∞	∞	∞	5
∞	16	-3	0	∞	4	14	2	-1
10	10	7	10	0	14	24	12	9
∞	12	13	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	2	∞	∞	∞	7	0	7
∞	∞	∞	∞	∞	∞	∞	-7	0

0	2	3	∞	∞	12	22	∞	7
∞	0	1	∞	∞	∞	∞	∞	6
∞	∞	0	∞	∞	∞	∞	∞	5
∞	3	-3	0	∞	4	9	2	-1
10	10	7	10	0	14	19	12	9
∞	12	13	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	2	∞	∞	∞	7	0	7
∞	-6	-5	∞	∞	∞	0	-7	0

0	1	2	∞	∞	12	7	0	7
∞	0	1	∞	∞	∞	6	-1	6
∞	-1	0	∞	∞	∞	5	-2	5
∞	-7	-6	0	∞	4	-1	-8	-1
10	3	4	10	0	14	9	2	9
∞	-11	-10	∞	∞	0	-5	-12	-5
∞	-5	-4	∞	∞	∞	0	-6	1
∞	1	2	∞	∞	∞	7	0	7
∞	-6	-5	∞	∞	∞	0	-7	0

Example 24

In[]:=

E21={{15,6},{19,4},{16,5},{29,4},{37,2},{36,8},{32,5},{35,5},{46,2},{42,5},{56,4},{76,2},{81,1},{85,4},{87,7},{94,1},{93,2}};ME21=ToWeightedAdjacencyMatrix[E21];gE21=ToEdgeWeightedGraph[E21];ME21//MatrixForm

Out[]//MatrixForm=

0	∞	∞	∞	6	5	∞	∞	4
∞	0	∞	∞	∞	∞	∞	∞	4
∞	5	0	∞	5	8	2	∞	∞
∞	5	∞	0	∞	2	∞	∞	∞
∞	∞	∞	∞	0	4	∞	∞	∞
∞	∞	∞	∞	∞	0	∞	∞	∞
∞	∞	∞	∞	∞	2	0	∞	∞
1	∞	∞	∞	4	∞	7	0	∞
∞	∞	2	1	∞	∞	∞	∞	0

In[]:=

Transpose@Prepend[Sort[Map[Flatten,E21/.EdgeToPair]],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	1	2	3	3	3	3	4	4	5	7	8	8	8	9	9
y	5	6	9	9	2	5	6	7	2	6	6	6	1	5	7	3	4
w	6	5	4	4	5	5	8	2	5	2	4	2	1	4	7	2	1

In[]:=

Graph[EdgeList[gE21],ImagePadding10,VertexLabels"Name"]

Out[]=

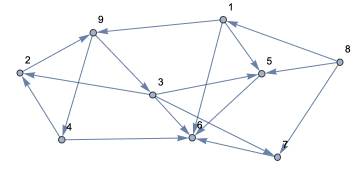
In[]:=

Floyd[gE21,FromWhereTableFalse]

★	1	2	3	4	5	6	7	8	9
1	0	10	6	5	6	5	8	∞	4
2	∞	0	6	5	11	7	8	∞	4
3	∞	5	0	10	5	4	2	∞	9
4	∞	5	11	0	16	2	13	∞	9
5	∞	∞	∞	∞	0	4	∞	∞	∞
6	∞	∞	∞	∞	∞	0	∞	∞	∞
7	∞	∞	∞	∞	∞	2	0	∞	∞
8	1	11	7	6	4	6	7	0	5
9	∞	6	2	1	7	3	4	∞	0

Example 25

In[]:=

E22={{18,4},{16,5},{14,3},{24,2},{38,7},{36,7},{45,4},{47,4},{58,2},{62,1},{65,3},{63,1},{74,5},{81,5},{82,1}};ME22=ToWeightedAdjacencyMatrix[E22];gE22=ToEdgeWeightedGraph[E22];ME22//MatrixForm

Out[]//MatrixForm=

0	∞	∞	3	∞	5	∞	4
∞	0	∞	2	∞	∞	∞	∞
∞	∞	0	∞	∞	7	∞	7
∞	∞	∞	0	4	∞	4	∞
∞	∞	∞	∞	0	∞	∞	2
∞	1	1	∞	3	0	∞	∞
∞	∞	∞	5	∞	∞	0	∞
5	1	∞	∞	∞	∞	∞	0

In[]:=

Transpose@Prepend[Sort[Map[Flatten,E22/.EdgeToPair]],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	1	2	3	3	4	4	5	6	6	6	7	8	8
y	4	6	8	4	6	8	5	7	8	2	3	5	4	1	2
w	3	5	4	2	7	7	4	4	2	1	1	3	5	5	1

In[]:=

Graph[EdgeList[gE22],ImagePadding10,VertexLabels"Name"]

Out[]=

In[]:=

Floyd[gE22,DistanceTableFalse]

★	1	2	3	4	5	6	7	8
1	★	82	63	14	45	16	47	18
2	81	★	63	24	45	16	47	58
3	81	62	★	24	65	36	47	38
4	81	82	63	★	45	16	47	58
5	81	82	63	24	★	16	47	58
6	81	62	63	24	65	★	47	58
7	81	82	63	74	45	16	★	58
8	81	82	63	24	45	16	47	★

Example 26

In[]:=

E23={{15,0},{16,4},{17,7},{19,5},{23,7},{28,5},{31,7},{32,6},{35,2},{36,3},{39,4},{46,5},{47,3},{53,4},{58,1},{59,1},{64,7},{69,7},{73,6},{92,5},{95,6},{97,6},{98,5}};ME23=ToWeightedAdjacencyMatrix[E23];gE23=ToEdgeWeightedGraph[E23,DirectedEdgesTrue];ME23//MatrixForm

Out[]//MatrixForm=

0	∞	∞	∞	0	4	7	∞	5
∞	0	7	∞	∞	∞	∞	5	∞
7	6	0	∞	2	3	∞	∞	4
∞	∞	∞	0	∞	5	3	∞	∞
∞	∞	4	∞	0	∞	∞	1	1
∞	∞	∞	7	∞	0	∞	∞	7
∞	∞	6	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	∞	0	∞
∞	5	∞	∞	6	∞	6	5	0

In[]:=

Transpose@Prepend[Sort[Map[Flatten,E23/.EdgeToPair]],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	1	1	2	2	3	3	3	3	3	4	4	5	5	5	6	6	7	9	9	9	9
y	5	6	7	9	3	8	1	2	5	6	9	6	7	3	8	9	4	9	3	2	5	7	8
w	0	4	7	5	7	5	7	6	2	3	4	5	3	4	1	1	7	7	6	5	6	6	5

In[]:=

Graph[EdgeList[gE23],ImagePadding10,VertexLabels"Name"]

Out[]=

In[]:=

Floyd[gE23,FromWhereTableFalse,TraceFalse]

★	1	2	3	4	5	6	7	8	9
1	0	6	4	11	0	4	7	1	1
2	14	0	7	17	9	10	16	5	10
3	7	6	0	10	2	3	9	3	3
4	16	15	9	0	11	5	3	12	12
5	11	6	4	14	0	7	7	1	1
6	23	12	16	7	13	0	10	12	7
7	13	12	6	16	8	9	0	9	9
8	∞	∞	∞	∞	∞	∞	∞	0	∞
9	17	5	10	20	6	13	6	5	0

Example 27

In[]:=

E24={{13,5},{24,5},{27,1},{28,3},{29,0},{35,3},{36,5},{46,1},{47,4},{56,4},{57,3},{58,2},{59,4},{64,2},{67,0},{69,5},{71,4},{73,5},{74,7},{85,3},{91,6},{92,3},{94,5},{95,6},{98,1}};ME24=ToWeightedAdjacencyMatrix[E24];gE24=ToEdgeWeightedGraph[E24,DirectedEdgesTrue];ME24//MatrixForm

Out[]//MatrixForm=

0	∞	5	∞	∞	∞	∞	∞	∞
∞	0	∞	5	∞	∞	1	3	0
∞	∞	0	∞	3	5	∞	∞	∞
∞	∞	∞	0	∞	1	4	∞	∞
∞	∞	∞	∞	0	4	3	2	4
∞	∞	∞	2	∞	0	0	∞	5
4	∞	5	7	∞	∞	0	∞	∞
∞	∞	∞	∞	3	∞	∞	0	∞
6	3	∞	5	6	∞	∞	1	0

In[]:=

Transpose@Prepend[Sort[Map[Flatten,E24/.EdgeToPair]],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	2	2	2	2	3	3	4	4	5	5	5	5	6	6	6	7	7	7	8	9	9	9	9	9
y	3	4	7	8	9	5	6	6	7	6	7	8	9	4	7	9	1	3	4	5	1	2	4	5	8
w	5	5	1	3	0	3	5	1	4	4	3	2	4	2	0	5	4	5	7	3	6	3	5	6	1

In[]:=

Graph[EdgeList[gE24],ImagePadding10,VertexLabels"Name"]

Out[]=

In[]:=

Floyd[gE24,DistanceTableTrue,FromWhereTableFalse]

★	1	2	3	4	5	6	7	8	9
1	0	15	5	12	8	10	10	10	12
2	5	0	6	5	4	6	1	1	0
3	9	10	0	7	3	5	5	5	7
4	5	9	6	0	9	1	1	7	6
5	7	7	8	6	0	4	3	2	4
6	4	8	5	2	8	0	0	6	5
7	4	15	5	7	8	8	0	10	12
8	10	10	11	9	3	7	6	0	7
9	6	3	9	5	4	6	4	1	0

Shortest Paths: FloydShortestPaths

Options

Alternatives for optional arguments: -- FromWhere -> All | any part specification of the list.

In[]:=

Options[FloydShortestPaths]

Out[]=

{FramedTrue,FromWhereAll,PrintTrue}

Example 28

In[]:=

E25={{{1,2},2},{{1,6},12},{{5,2},17},{{2,3},1},{{2,8},1},{{3,1},-4},{{9,6},4},{{4,3},3},{{4,6},4},{{4,8},12},{{5,1},8},{{5,4},10},{{6,2},12},{{6,3},12},{{6,7},10},{{8,7},7}};ME25=ToWeightedAdjacencyMatrix[E25];gE25=ToEdgeWeightedGraph[E25];ME25//MatrixForm

Out[]//MatrixForm=

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	1	∞
-4	∞	0	∞	∞	∞	∞	∞	∞
∞	∞	3	0	∞	4	∞	12	∞
8	17	∞	10	0	∞	∞	∞	∞
∞	12	12	∞	∞	0	10	∞	∞
∞	∞	∞	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	4	∞	∞	0

In[]:=

Transpose@Prepend[Sort[Flatten/@E25],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	2	2	3	4	4	4	5	5	5	6	6	6	8	9
y	2	6	3	8	1	3	6	8	1	2	4	2	3	7	7	6
w	2	12	1	1	-4	3	4	12	8	17	10	12	12	10	7	4

In[]:=

FloydShortestPaths[E25]

Out[]=

Found cycle of negative weight

{{31,-4},{12,2},{23,1}}

Example 29

In[]:=

E26={{{1,2},2},{{1,6},12},{{5,2},10},{{2,3},1},{{8,2},1},{{4,3},-3},{{4,6},4},{{4,8},2},{{5,1},10},{{5,4},10},{{6,9},-5},{{6,2},12},{{3,9},5},{{6,7},10},{{7,9},1},{{8,7},7},{{9,8},-7}};ME26=ToWeightedAdjacencyMatrix[E26];gE26=ToEdgeWeightedGraph[E26];ME26//MatrixForm

Out[]//MatrixForm=

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	∞	∞
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	∞
10	10	∞	10	0	∞	∞	∞	∞
∞	12	∞	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	∞	∞	-7	0

In[]:=

Transpose@Prepend[Sort[Flatten/@E26],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	2	3	4	4	4	5	5	5	6	6	6	7	8	8	9
y	2	6	3	9	3	6	8	1	2	4	2	7	9	9	2	7	8
w	2	12	1	5	-3	4	2	10	10	10	12	10	-5	1	1	7	-7

In[]:=

FloydShortestPaths[ME26,FromWhere{1}]

{{16,12},{69,-5}}

{{16,12},{69,-5},{98,-7}}

{{16,12},{69,-5},{98,-7},{82,1}}

{{16,12},{69,-5},{98,-7},{87,7}}

{{16,12},{69,-5},{98,-7},{82,1},{23,1}}

In[]:=

FloydShortestPaths[ME26,FromWhere3;;5]

{{39,5},{98,-7}}

{{39,5},{98,-7},{82,1}}

{{39,5},{98,-7},{87,7}}

{{46,4},{69,-5}}

{{46,4},{69,-5},{98,-7}}

{{46,4},{69,-5},{98,-7},{82,1}}

{{46,4},{69,-5},{98,-7},{87,7}}

{{46,4},{69,-5},{98,-7},{82,1},{23,1}}

{{54,10},{46,4}}

{{54,10},{46,4},{69,-5}}

{{54,10},{46,4},{69,-5},{98,-7}}

{{54,10},{46,4},{69,-5},{98,-7},{82,1}}

{{54,10},{46,4},{69,-5},{98,-7},{87,7}}

{{54,10},{46,4},{69,-5},{98,-7},{82,1},{23,1}}

In[]:=

FloydShortestPaths[ME26,FromWhere;;2]

{{16,12},{69,-5}}

{{16,12},{69,-5},{98,-7}}

{{16,12},{69,-5},{98,-7},{82,1}}

{{16,12},{69,-5},{98,-7},{87,7}}

{{16,12},{69,-5},{98,-7},{82,1},{23,1}}

{{23,1},{39,5}}

{{23,1},{39,5},{98,-7}}

{{23,1},{39,5},{98,-7},{87,7}}

In[]:=

FloydShortestPaths[ME26,FromWhere{3,6}]

{{39,5},{98,-7}}

{{39,5},{98,-7},{82,1}}

{{39,5},{98,-7},{87,7}}

{{69,-5},{98,-7}}

{{69,-5},{98,-7},{82,1}}

{{69,-5},{98,-7},{87,7}}

{{69,-5},{98,-7},{82,1},{23,1}}

Example 30

In[]:=

E27={{15,6},{19,4},{16,5},{29,4},{37,2},{36,8},{32,5},{35,5},{46,2},{42,5},{56,4},{76,2},{81,1},{85,4},{87,7},{94,1},{93,2}};ME27=ToWeightedAdjacencyMatrix[E27];gE27=ToEdgeWeightedGraph[E27];ME27//MatrixForm

Out[]//MatrixForm=

0	∞	∞	∞	6	5	∞	∞	4
∞	0	∞	∞	∞	∞	∞	∞	4
∞	5	0	∞	5	8	2	∞	∞
∞	5	∞	0	∞	2	∞	∞	∞
∞	∞	∞	∞	0	4	∞	∞	∞
∞	∞	∞	∞	∞	0	∞	∞	∞
∞	∞	∞	∞	∞	2	0	∞	∞
1	∞	∞	∞	4	∞	7	0	∞
∞	∞	2	1	∞	∞	∞	∞	0

In[]:=

Transpose@Prepend[Sort[Flatten/@(E27/.EdgeToPair)],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	1	2	3	3	3	3	4	4	5	7	8	8	8	9	9
y	5	6	9	9	2	5	6	7	2	6	6	6	1	5	7	3	4
w	6	5	4	4	5	5	8	2	5	2	4	2	1	4	7	2	1

In[]:=

FloydShortestPaths[gE27,FromWhere{1,5,8}]

{{19,4},{93,2}}

{{19,4},{94,1}}

{{19,4},{93,2},{37,2}}

{{19,4},{94,1},{42,5}}

{{81,1},{16,5}}

{{81,1},{19,4}}

{{81,1},{19,4},{93,2}}

{{81,1},{19,4},{94,1}}

{{81,1},{19,4},{94,1},{42,5}}

Example 31

In[]:=

E28={{18,4},{16,5},{14,3},{24,2},{38,7},{36,7},{45,4},{47,4},{58,2},{62,1},{65,3},{63,1},{74,5},{81,5},{82,1}};ME28=ToWeightedAdjacencyMatrix[E28];gE28=ToEdgeWeightedGraph[E28];ME28//MatrixForm

Out[]//MatrixForm=

0	∞	∞	3	∞	5	∞	4
∞	0	∞	2	∞	∞	∞	∞
∞	∞	0	∞	∞	7	∞	7
∞	∞	∞	0	4	∞	4	∞
∞	∞	∞	∞	0	∞	∞	2
∞	1	1	∞	3	0	∞	∞
∞	∞	∞	5	∞	∞	0	∞
5	1	∞	∞	∞	∞	∞	0

In[]:=

Transpose@Prepend[Sort[Flatten/@(E28/.EdgeToPair)],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	1	2	3	3	4	4	5	6	6	6	7	8	8
y	4	6	8	4	6	8	5	7	8	2	3	5	4	1	2
w	3	5	4	2	7	7	4	4	2	1	1	3	5	5	1

In[]:=

FloydShortestPaths[ME28,FromWhere6;;7]

{{62,1},{24,2}}

{{65,3},{58,2}}

{{62,1},{24,2},{47,4}}

{{65,3},{58,2},{81,5}}

{{74,5},{45,4}}

{{74,5},{45,4},{58,2}}

{{74,5},{45,4},{58,2},{81,5}}

{{74,5},{45,4},{58,2},{82,1}}

{{74,5},{45,4},{58,2},{81,5},{16,5}}

{{74,5},{45,4},{58,2},{81,5},{16,5},{63,1}}

Example 32

In[]:=

E29={{15,0},{16,4},{17,7},{19,5},{23,7},{28,5},{31,7},{32,6},{35,2},{36,3},{39,4},{46,5},{47,3},{53,4},{58,1},{59,1},{64,7},{69,7},{73,6},{92,5},{95,6},{97,6},{98,5}};ME29=ToWeightedAdjacencyMatrix[E29];gE29=ToEdgeWeightedGraph[E29,DirectedEdgesTrue];ME29//MatrixForm

Out[]//MatrixForm=

0	∞	∞	∞	0	4	7	∞	5
∞	0	7	∞	∞	∞	∞	5	∞
7	6	0	∞	2	3	∞	∞	4
∞	∞	∞	0	∞	5	3	∞	∞
∞	∞	4	∞	0	∞	∞	1	1
∞	∞	∞	7	∞	0	∞	∞	7
∞	∞	6	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	∞	0	∞
∞	5	∞	∞	6	∞	6	5	0

In[]:=

Transpose@Prepend[Sort[Flatten/@(E29/.EdgeToPair)],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	1	1	1	2	2	3	3	3	3	3	4	4	5	5	5	6	6	7	9	9	9	9
y	5	6	7	9	3	8	1	2	5	6	9	6	7	3	8	9	4	9	3	2	5	7	8
w	0	4	7	5	7	5	7	6	2	3	4	5	3	4	1	1	7	7	6	5	6	6	5

In[]:=

FloydShortestPaths[ME29,FromWhere6;;7]

{{64,7},{47,3}}

{{69,7},{92,5}}

{{69,7},{95,6}}

{{69,7},{98,5}}

{{64,7},{47,3},{73,6}}

{{64,7},{47,3},{73,6},{31,7}}

{{73,6},{31,7}}

{{73,6},{32,6}}

{{73,6},{35,2}}

{{73,6},{36,3}}

{{73,6},{35,2},{58,1}}

{{73,6},{35,2},{59,1}}

{{73,6},{36,3},{64,7}}

Example 33

In[]:=

E30={{13,5},{24,5},{27,1},{28,3},{29,0},{35,3},{36,5},{46,1},{47,4},{56,4},{57,3},{58,2},{59,4},{64,2},{67,0},{69,5},{71,4},{73,5},{74,7},{85,3},{91,6},{92,3},{94,5},{95,6},{98,1}};ME30=ToWeightedAdjacencyMatrix[E30];gE30=ToEdgeWeightedGraph[E30,DirectedEdgesTrue];ME30//MatrixForm

Out[]//MatrixForm=

0	∞	5	∞	∞	∞	∞	∞	∞
∞	0	∞	5	∞	∞	1	3	0
∞	∞	0	∞	3	5	∞	∞	∞
∞	∞	∞	0	∞	1	4	∞	∞
∞	∞	∞	∞	0	4	3	2	4
∞	∞	∞	2	∞	0	0	∞	5
4	∞	5	7	∞	∞	0	∞	∞
∞	∞	∞	∞	3	∞	∞	0	∞
6	3	∞	5	6	∞	∞	1	0

In[]:=

Transpose@Prepend[Sort[Flatten/@(E30/.EdgeToPair)],{"x","y","w"}]//Grid[#,DividersAll]&

Out[]=

x	1	2	2	2	2	3	3	4	4	5	5	5	5	6	6	6	7	7	7	8	9	9	9	9	9
y	3	4	7	8	9	5	6	6	7	6	7	8	9	4	7	9	1	3	4	5	1	2	4	5	8
w	5	5	1	3	0	3	5	1	4	4	3	2	4	2	0	5	4	5	7	3	6	3	5	6	1

In[]:=

FloydShortestPaths[ME30,FromWhere;;2]

{{13,5},{35,3}}

{{13,5},{36,5}}

{{13,5},{35,3},{58,2}}

{{13,5},{35,3},{59,4}}

{{13,5},{36,5},{64,2}}

{{13,5},{36,5},{67,0}}

{{13,5},{35,3},{59,4},{92,3}}

{{24,5},{46,1}}

{{27,1},{71,4}}

{{27,1},{73,5}}

{{29,0},{98,1}}

{{29,0},{98,1},{85,3}}

EulerTourQ and EulerTour

Alternatives for optional argument of EulerTourQ:-- Trace -> True | False

In[]:=

Options[EulerTourQ]

Out[]=

{TraceFalse}

Alternatives for optional arguments : -- FontSize -> 10 | any font size,-- GraphLayout  Automatic | any Graph layout,-- ImagePadding  15,-- ImageSize  Automatic | {450, 150} | any dimensions,-- ItemSize -> Automatic | {2, 4, 2, 2, 28, 2} | {s1, s2, s3, s4, s5, s6},-- ManipulateTour -> True |False,-- ManipulateWalk -> False | True,-- SelectionRule  First | Last | RandomChoice,-- Spacings -> Automatic | {s1, Automatic} | {s1, s2},-- TableBreaks → False | integer | {integers},-- TourStyle -> {Automatic | Thick | Thin | Thickness[ _ ], Red | color specification },-- TourType  Vertices | UndirectedEdges | DirectedEdges | Rule | Pairs | None,-- Trace -> True | False,-- SelectedVertexSize -> Automatic | Tiny | Small | Medium | Large | RealNumber,-- SelectedVertexStyle -> Automatic | color specification.

In[]:=

Options[EulerTour]

Out[]=

FontSize10,GraphLayoutAutomatic,ImagePadding15,ImageSizeAutomatic,ItemSizeAutomatic,ManipulateTourTrue,ManipulateWalkFalse,SelectedVertexSizeAutomatic,SelectedVertexStyleAutomatic,SelectionRuleFirst,Spacings{1,Automatic},TableBreaksFalse,TourStyleThickness[Large],

,TourFormatVertices,TraceReduce,VertexCoordinatesAutomatic

Example 34

In[]:=

E31={{6,3},{3,11},{6,9},{9,1},{7,11},{3,7},{2,7},{7,12},{12,8},{2,8},{4,11},{11,5},{5,1},{10,3},{4,9}};ME31=ToWeightedAdjacencyMatrix[E31,∞];gE31=ToGraph[E31,∞];

In[]:=

EulerTourQ[ME31,TraceTrue]

Vertices and their degrees:

{{1,2},{2,2},{3,4},{4,2},{5,2},{6,2},{7,4},{8,2},{9,3},{10,1},{11,4},{12,2}}

There exists Euler tour between vertices 9 and 10

In[]:=

EulerTour[gE31,10,ItemSizeAutomatic,ManipulateWalkTrue,TraceTrue,TableBreaks8,SelectionRuleRandomChoice]

{10,3,7,12,8,2,7,11,4,9,6,3,11,5,1,9}

v 1	e	v 2	c(e)	Σ ⋃ Ω	Σ
10	{10,3}	3	1	{10,3}	2
3	{3,7}	7	1	{10,3,7}	3
7	{7,11}	11	1	{10,3,7,11}	4
11	{4,11}	4	1	{10,3,7,11,4}	5
4	{4,9}	9	1	{10,3,7,11,4,9}	6
9	{6,9}	6	1	{10,3,7,11,4,9,6}	7
6	{6,3}	3	1	{10,3,7,11,4,9,6,3}	8
3	{3,11}	11	1	{10,3,7,11,4,9,6,3,11}	9

v 1	e	v 2	c(e)	Σ ⋃ Ω	Σ
11	{11,5}	5	1	{10,3,7,11,4,9,6,3,11,5}	10
5	{5,1}	1	1	{10,3,7,11,4,9,6,3,11,5,1}	11
1	{9,1}	9	1	{10,3,7,11,4,9,6,3,11,5,1,9}	12
1	{9,1}	9	-1	{10,3,7,11,4,9,6,3,11,5,1} ⋃ {1,9}	11
5	{5,1}	1	-1	{10,3,7,11,4,9,6,3,11,5} ⋃ {5,1,1,9}	10
11	{11,5}	5	-1	{10,3,7,11,4,9,6,3,11} ⋃ {11,5,5,1,1,9}	9
3	{3,11}	11	-1	{10,3,7,11,4,9,6,3} ⋃ {3,11,11,5,5,1,1,9}	8
6	{6,3}	3	-1	{10,3,7,11,4,9,6} ⋃ {6,3,3,11,11,5,5,1,1,9}	7

v 1	e	v 2	c(e)	Σ ⋃ Ω	Σ
9	{6,9}	6	-1	{10,3,7,11,4,9} ⋃ {9,6,6,3,3,11,11,5,5,1,1,9}	6
4	{4,9}	9	-1	{10,3,7,11,4} ⋃ {4,9,9,6,6,3,3,11,11,5,5,1,1,9}	5
11	{4,11}	4	-1	{10,3,7,11} ⋃ {11,4,4,9,9,6,6,3,3,11,11,5,5,1,1,9}	4
7	{7,11}	11	-1	{10,3,7} ⋃ {7,11,11,4,4,9,9,6,6,3,3,11,11,5,5,1,1,9}	3
7	{7,12}	12	1	{10,3,7,12} ⋃ {7,11,11,4,4,9,9,6,6,3,3,11,11,5,5,1,1,9}	4
12	{12,8}	8	1	{10,3,7,12,8} ⋃ {7,11,11,4,4,9,9,6,6,3,3,11,11,5,5,1,1,9}	5
8	{2,8}	2	1	{10,3,7,12,8,2} ⋃ {7,11,11,4,4,9,9,6,6,3,3,11,11,5,5,1,1,9}	6
2	{2,7}	7	1	{10,3,7,12,8,2,7,11,4,9,6,3,11,5,1,9}	16

{103,37,712,128,82,27,711,114,49,96,63,311,115,51,19}

{103,37,711,114,49,96,63,311,115,51,19,91,15,511,113,36,69,94,411,117,712,128,82,27,711,114,49,96,63,311,115,51,19}

Example 35

In[]:=

E32={{1,11},{1,7},{11,12},{12,1},{1,2},{2,3},{3,4},{4,5},{13,14},{14,4},{5,6},{1,5},{6,4},{2,5},{3,6},{2,7},{5,7},{3,8},{6,8},{9,8},{7,10},{10,8},{11,9},{11,8}};ME32=ToWeightedAdjacencyMatrix[E32,∞];gE32=ToGraph[E32,∞,GraphLayoutAutomatic]

Out[]=

In[]:=

EulerTourQ[E32,TraceTrue]

Vertices and their degrees:

{{1,5},{2,4},{3,4},{4,4},{5,5},{6,4},{7,4},{8,5},{9,2},{10,2},{11,4},{12,2},{13,1},{14,2}}

There exists no Euler tour

In[]:=

EulerTour[gE32,1,ItemSize{2,4,2,2,26,2},ManipulateTourFalse,ManipulateWalkFalse,SelectionRuleLast,TraceFalse,TableBreaks12]

{1,5,7,10,8,11,9,8,6,3,4,6,5,4,14,13}

Example 36

In[]:=

E33={{1,2},{2,3},{3,4},{1,5},{5,6},{6,4},{2,5},{3,6},{2,7},{5,7},{3,8},{6,8},{7,9},{9,8},{7,10},{10,8},{5,10},{10,3},{3,11},{11,5},{1,11},{11,4},{4,7},{7,1}};ME33=ToWeightedAdjacencyMatrix[E31,∞];gE33=ToGraph[E33];

In[]:=

EulerTourQ[E33]

There exists closed Euler tour on any vertex

In[]:=

EulerTour[E33,2,ManipulateWalkTrue,ManipulateTourTrue,SelectionRuleRandomChoice,TraceReduce,VertexCoordinatesEllipse[5,3]]

{2,5,7,4,6,3,4,11,1,5,11,3,2,1,7,9,8,6,5,10,3,8,10,7,2}

v 1	e	v 2	c(e)	Σ ⋃ Ω	Σ
7	{2,7}	2	1	{2,5,7,4,6,3,4,11,1,5,11,3,2,1,7,2}	16
7	{2,7}	2	-1	{2,5,7,4,6,3,4,11,1,5,11,3,2,1,7} ⋃ {7,2}	15
10	{7,10}	7	1	{2,5,7,4,6,3,4,11,1,5,11,3,2,1,7,9,8,6,5,10,7,2}	22
10	{7,10}	7	-1	{2,5,7,4,6,3,4,11,1,5,11,3,2,1,7,9,8,6,5,10} ⋃ {10,7,7,2}	20
8	{10,8}	10	1	{2,5,7,4,6,3,4,11,1,5,11,3,2,1,7,9,8,6,5,10,3,8,10,7,2}	25

{25,57,74,46,63,34,411,111,15,511,113,32,21,17,79,98,86,65,510,103,38,810,107,72}

{25,57,74,46,63,34,411,111,15,511,113,32,21,17,72,27,79,98,86,65,510,107,72,27,710,103,38,810,107,72}

Example 37

In[]:=

E34={{1,2},{1,16},{2,3},{2,21},{3,11},{3,13},{4,5},{5,6},{5,7},{5,12},{5,17},{6,7},{7,8},{8,9},{8,20},{9,10},{9,19},{10,5},{10,7},{10,11},{11,4},{11,13},{12,3},{13,2},{13,10},{13,14},{14,10},{15,14},{15,16},{16,13},{16,14},{17,18},{18,8},{19,15},{20,9},{21,1},{21,22},{22,1},{22,15}};

In[]:=

EulerTourQ[E34,TraceTrue]

Vertices and their degrees:

{{1,4},{2,4},{3,4},{4,2},{5,6},{6,2},{7,4},{8,4},{9,4},{10,6},{11,4},{12,2},{13,6},{14,4},{15,4},{16,4},{17,2},{18,2},{19,2},{20,2},{21,3},{22,3}}

There exists Euler tour between vertices 21 and 22

In[]:=

EulerTour[E34,21,ManipulateWalkTrue,ManipulateTourFalse,SelectionRuleLast,TraceTrue,TableBreaks8]

{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10,9,8,7,6,5,4,11,3,2,1,22}

v 1	e	v 2	c(e)	Σ ⋃ Ω	Σ
21	{21,22}	22	1	{21,22}	2
22	{22,15}	15	1	{21,22,15}	3
15	{19,15}	19	1	{21,22,15,19}	4
19	{9,19}	9	1	{21,22,15,19,9}	5
9	{20,9}	20	1	{21,22,15,19,9,20}	6
20	{8,20}	8	1	{21,22,15,19,9,20,8}	7
8	{18,8}	18	1	{21,22,15,19,9,20,8,18}	8
18	{17,18}	17	1	{21,22,15,19,9,20,8,18,17}	9

v 1	e	v 2	c(e)	Σ ⋃ Ω	Σ
17	{5,17}	5	1	{21,22,15,19,9,20,8,18,17,5}	10
5	{10,5}	10	1	{21,22,15,19,9,20,8,18,17,5,10}	11
10	{14,10}	14	1	{21,22,15,19,9,20,8,18,17,5,10,14}	12
14	{16,14}	16	1	{21,22,15,19,9,20,8,18,17,5,10,14,16}	13
16	{16,13}	13	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13}	14
13	{13,14}	14	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14}	15
14	{15,14}	15	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15}	16
15	{15,16}	16	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16}	17

v 1	e	v 2	c(e)	Σ ⋃ Ω	Σ
16	{1,16}	1	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1}	18
1	{22,1}	22	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,22}	19
1	{22,1}	22	-1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1} ⋃ {1,22}	18
1	{21,1}	21	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21} ⋃ {1,22}	19
21	{2,21}	2	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2} ⋃ {1,22}	20
2	{13,2}	13	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13} ⋃ {1,22}	21
13	{13,10}	10	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10} ⋃ {1,22}	22
10	{10,11}	11	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11} ⋃ {1,22}	23

v 1	e	v 2	c(e)	Σ ⋃ Ω	Σ
11	{11,13}	13	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13} ⋃ {1,22}	24
13	{3,13}	3	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3} ⋃ {1,22}	25
3	{12,3}	12	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12} ⋃ {1,22}	26
12	{5,12}	5	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5} ⋃ {1,22}	27
5	{5,7}	7	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7} ⋃ {1,22}	28
7	{10,7}	10	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10} ⋃ {1,22}	29
10	{9,10}	9	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10,9} ⋃ {1,22}	30
9	{8,9}	8	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10,9,8} ⋃ {1,22}	31

v 1	e	v 2	c(e)	Σ ⋃ Ω	Σ
8	{7,8}	7	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10,9,8,7} ⋃ {1,22}	32
7	{6,7}	6	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10,9,8,7,6} ⋃ {1,22}	33
6	{5,6}	5	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10,9,8,7,6,5} ⋃ {1,22}	34
5	{4,5}	4	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10,9,8,7,6,5,4} ⋃ {1,22}	35
4	{11,4}	11	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10,9,8,7,6,5,4,11} ⋃ {1,22}	36
11	{3,11}	3	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10,9,8,7,6,5,4,11,3} ⋃ {1,22}	37
3	{2,3}	2	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10,9,8,7,6,5,4,11,3,2} ⋃ {1,22}	38
2	{1,2}	1	1	{21,22,15,19,9,20,8,18,17,5,10,14,16,13,14,15,16,1,21,2,13,10,11,13,3,12,5,7,10,9,8,7,6,5,4,11,3,2,1,22}	40

{2122,2215,1519,199,920,208,818,1817,175,510,1014,1416,1613,1314,1415,1516,161,122,221,121,212,213,1310,1011,1113,133,312,125,57,710,109,98,87,76,65,54,411,113,32,21,122}

Example 38

In[]:=

E35={{11,2},{7,6},{5,9},{8,12},{8,2},{9,10},{8,4},{12,5},{7,12},{5,1},{9,1},{3,10},{3,1},{3,8},{10,6},{4,10},{3,7},{8,5},{12,3},{2,6},{7,2},{12,9},{7,8},{1,12},{11,3},{6,8},{11,7}}

Out[]=

{{11,2},{7,6},{5,9},{8,12},{8,2},{9,10},{8,4},{12,5},{7,12},{5,1},{9,1},{3,10},{3,1},{3,8},{10,6},{4,10},{3,7},{8,5},{12,3},{2,6},{7,2},{12,9},{7,8},{1,12},{11,3},{6,8},{11,7}}

In[]:=

EulerTourQ[E35]

There exists Euler tour between vertices 8 and 11

In[]:=

EulerTour[E35,8,ManipulateWalkTrue,ManipulateTourFalse,SelectionRuleFirst,TraceReduce,VertexCoordinatesEllipse[6,3]]

{8,12,5,9,10,3,1,5,8,2,11,3,8,4,10,6,7,12,9,1,12,3,7,2,6,8,7,11}

v 1	e	v 2	c(e)	Σ ⋃ Ω	Σ
7	{11,7}	11	1	{8,12,5,9,10,3,1,5,8,2,11,3,8,4,10,6,7,12,3,7,2,6,8,7,11}	25
12	{12,3}	3	-1	{8,12,5,9,10,3,1,5,8,2,11,3,8,4,10,6,7,12} ⋃ {12,3,3,7,7,2,2,6,6,8,8,7,7,11}	18
1	{1,12}	12	1	{8,12,5,9,10,3,1,5,8,2,11,3,8,4,10,6,7,12,9,1,12,3,7,2,6,8,7,11}	28

{812,125,59,910,103,31,15,58,82,211,113,38,84,410,106,67,712,123,37,72,26,68,87,711,117,78,86,62,27,73,312,129,91,112,123,37,72,26,68,87,711}

Pairing in Bipartite (Dissected) Graphs

AugmentingPath

Alternatives for optional arguments of AugmentigPath:-- AugmentedPairing ->True | False,-- AugmentingPath -> True | False,-- FromWhere -> True | False,-- FontSize -> 10 | Any font size,-- ImageSize -> Automatic | {450, 150} | Any dimensions,-- ImagePadding -> 10 | Any size,-- ItemSize -> Automatic | List, -- Manipulate -> True | False,-- SelectionRule  First | Last | RandomChoice,-- Sort -> True | False,-- Spacings -> Automatic | {0.5, 0,8} | as for Grid-- Trace -> True | Reduce | False,-- VertexCoordinates  Automatic | “XY” | Orthogon[positive number].

In[]:=

Options[AugmentingPath]

Out[]=

{AugmentedPairingTrue,AugmentingPathTrue,FontSize10,FromWhereTrue,ImageSizeAutomatic,ImagePadding10,ItemSizeAutomatic,ManipulateTrue,SelectionRuleFirst,SortFalse,Spacings{1,0.75},TraceTrue,VertexCoordinatesAutomatic}

MaxPairing

Alternatives for optional arguments of MaxPairing:-- FontSize -> 10 | any font size,-- ItemSize -> Automatic | List, -- Print => All | Last,-- SelectionRule  First | Last | RandomChoice,-- Sort -> True | False,-- Spacings -> Automatic | {0.5, 0,8} | {number | Automatic, number | Automatic} | number,-- Trace -> True | Reduce | False.

In[]:=

Options[MaxPairing]

Out[]=

{AugmentedPairingTrue,AugmentingPathTrue,FontSize10,FromWhereTrue,ItemSizeAutomatic,PrintAll,SelectionRuleFirst,SortFalse,Spacings{1,0.75},TraceTrue}

Example 39: X = Range[1, 7], Y = Range[8, 15]

In[]:=

X36=Range[1,7];Y36=Range[8,15];E36={{1,10},{1,11},{2,8},{2,9},{3,8},{3,9},{3,11},{4,12},{4,13},{4,14},{4,15},{5,9},{5,10},{5,12},{6,8},{6,13},{7,11},{7,14}};P36={110,28,39,412,711};gE36=ToGraph[E36,∞];ToGraph[E36,∞,EdgeStyleMap[#{Thick,Green}&,P36],GraphLayoutAutomatic,VertexCoordinatesOrthogon[7,8,1],VertexLabels->OrthogonLabels[7,8],ImagePadding10,ImageSize{450,150}]

Out[]=

In[]:=

{DissectedGraphQ[gE36,X36,Y36],MaxPairingLength[gE36,X36]}

Out[]=

{True,7}

In[]:=

P36={110,28,39,412,711};AugmentingPath[gE36,X36,Y36,P36,SelectionRuleFirst,VertexCoordinatesOrthogon[1],TraceTrue]

Initial pairing:

{110,28,39,412,711}

Extension of initial pairing found in a trivial way:

{110,28,39,412,711,613}

Mx	x	xy	y	zy	z	Mz	FromWhere
{5}
∅	5	59	9	39	3	{3}	{59,93}
∅	5	510	10	110	1	{3,1}	{510,101}
∅	5	512	12	412	4	{3,1,4}	{512,124}
{3,1,4}
{1,4}	3	38	8	28	2	{2}	{38,82}
{1,4}	3	311	11	711	7	{2,7}	{311,117}
∅	4	413	13	613	6	{2,7,6}	{413,136}
∅	4	414	14			{2,7,6}	{414}
∅

FromWhereList:

{59,39,510,110,512,412,38,28,311,711,413,613,414}

Augmenting Path:

{512,412,414}

Augmented Pairing:

{110,28,39,711,613,512,414}

In[]:=

AugmentingPath[E36,X36,Y36,SelectionRuleFirst,VertexCoordinatesOrthogon[1],TraceReduce]

A pairing found in a trivial way:

{110,28,39,412,613,711}

Mx	x	xy	y	zy	z	Mz	FromWhere
∅	5	59	9	39	3	{3}	{59,93}
∅	5	510	10	110	1	{3,1}	{510,101}
∅	5	512	12	412	4	{3,1,4}	{512,124}
{1,4}	3	38	8	28	2	{2}	{38,82}
{1,4}	3	311	11	711	7	{2,7}	{311,117}
∅	4	413	13	613	6	{2,7,6}	{413,136}
∅	4	414	14			{2,7,6}	{414}

FromWhereList:

{59,39,510,110,512,412,38,28,311,711,413,613,414}

Augmenting Path:

{512,412,414}

Augmented Pairing:

{110,28,39,613,711,512,414}

GraphAlgorithms`Private`n

In[]:=

MaxPairing[E36,X36,Y36,P36,AugmentingPathTrue,AugmentedPairingTrue,SelectionRuleLast,FromWhereTrue,TraceTrue]

Initial pairing:

{110,28,39,412,711}

Extension of initial pairing found in a trivial way:

{110,28,39,412,711,613}

Mx	x	xy	y	zy	z	Mz	FromWhere
{5}
∅	5	512	12	412	4	{4}	{512,124}
∅	5	510	10	110	1	{4,1}	{510,101}
∅	5	59	9	39	3	{4,1,3}	{59,93}
{4,1,3}
{4,1}	3	311	11	711	7	{7}	{311,117}
{4,1}	3	38	8	28	2	{7,2}	{38,82}
∅	4	415	15			{7,2}	{415}
∅

FromWhereList:

{512,124,510,101,59,93,311,117,38,82,415}

Augmenting Path:

{512,412,415}

Augmented Pairing:

{110,28,39,711,613,512,415}

***

The last pairing is maximal.

Example 40: X = Range[1, 7], Y = Range[8, 15]

In[]:=

X37=Range[1,7];Y37=Range[8,15];E37={{1,11},{1,12},{1,14},{1,15},{2,8},{2,11},{2,15},{3,9},{3,11},{3,12},{3,14},{4,12},{4,13},{4,14},{5,9},{5,10},{5,11},{5,12},{6,10},{6,11},{6,12},{6,9},{7,8},{7,9},{7,10},{7,11}};E37={{1,11},{1,12},{1,14},{1,15},{2,8},{2,11},{2,15},{3,9},{3,11},{3,12},{3,14},{4,12},{4,13},{4,14},{5,10},{5,11},{5,12},{6,10},{6,11},{6,12},{7,10},{7,11}};P37={111,28,39,412,510};gE37=ToGraph[E37,∞];ToGraph[E37,∞,EdgeStyleMap[#{Thick,Green}&,P37],GraphLayoutAutomatic,VertexCoordinatesOrthogon[7,8,1],VertexLabels->OrthogonLabels[7,8],ImagePadding10]

Out[]=

In[]:=

{DissectedGraphQ[gE37,X37,Y37],MaxPairingLength[gE37,X37]}

Out[]=

{True,7}

In[]:=

P37={111,28,39,412,510};AugmentingPath[E37,X37,Y37,P37,SelectionRuleLast,ManipulateTrue,TraceTrue,VertexCoordinates"XY"]

Initial pairing:

{111,28,39,412,510}

Mx	x	xy	y	zy	z	Mz	FromWhere
{6,7}
{6}	7	711	11	111	1	{1}	{711,111}
{6}	7	710	10	510	5	{1,5}	{710,105}
∅	6	612	12	412	4	{1,5,4}	{612,124}
{1,5,4}
{1,5}	4	414	14			∅	{414}
∅	1	115	15			∅	{115}
∅

FromWhereList:

{711,111,710,510,612,412,414,115}

Augmenting Path:

{711,111,115}

Augmented Pairing:

{28,39,412,510,711,115}

In[]:=

AugmentingPath[E37,X37,Y37,SelectionRuleLast,ManipulateTrue,TraceTrue,VertexCoordinates"XY"]

A pairing found in a trivial way:

{711,612,510,414,39,215}

Mx	x	xy	y	zy	z	Mz	FromWhere
{1}
∅	1	115	15	215	2	{2}	{115,152}
∅	1	114	14	414	4	{2,4}	{114,144}
∅	1	112	12	612	6	{2,4,6}	{112,126}
∅	1	111	11	711	7	{2,4,6,7}	{111,117}
{2,4,6,7}
{2,4,6}	7	710	10	510	5	{5}	{710,105}
{2}	4	413	13			{5}	{413}
∅	2	28	8			∅	{28}
∅

FromWhereList:

{115,215,114,414,112,612,111,711,710,510,413,28}

Augmenting Path:

{115,215,28}

Augmented Pairing:

{711,612,510,414,39,115,28}

In[]:=

MaxPairing[E37,X37,Y37,FromWhereTrue,TraceTrue,PrintAll]

Extension of initial pairing found in a trivial way:

{111,28,39,412,510}

Mx	x	xy	y	zy	z	Mz	FromWhere
{6,7}
{7}	6	610	10	510	5	{5}	{610,105}
{7}	6	611	11	111	1	{5,1}	{611,111}
{7}	6	612	12	412	4	{5,1,4}	{612,124}
{5,1,4}
{4}	1	114	14			∅	{114}
∅	4	413	13			∅	{413}
∅

FromWhereList:

{610,105,611,111,612,124,114,413}

Augmenting Path:

{612,412,413}

Augmented Pairing:

{111,28,39,510,612,413}

***

Mx	x	xy	y	zy	z	Mz	FromWhere
{7}
∅	7	710	10	510	5	{5}	{710,105}
∅	7	711	11	111	1	{5,1}	{711,111}
{5,1}
{1}	5	512	12	612	6	{6}	{512,126}
∅	1	114	14			{6}	{114}
∅

FromWhereList:

{710,105,711,111,512,126,114}

Augmenting Path:

{711,111,114}

Augmented Pairing:

{28,39,510,612,413,711,114}

***

The last pairing is maximal.

In[]:=

MaxPairingLength[gE37,X37]

Out[]=

Example 41: X = Range[1, 7], Y = Range[8, 14]

In[]:=

X38=Range[1,7];Y38=Range[8,14];E38={{1,11},(*{1,12},{1,14},{1,15},*){2,8},(*{2,11},{2,15},*){3,9},{3,11},{3,12},{3,14},{4,12},{4,13},{4,14},{5,9},{5,10},{5,11},(*{5,12},{6,10},{6,11},*){6,12},{6,9},{7,8},{7,9},{7,10},{7,11}};ME38=ToWeightedAdjacencyMatrix[E38,∞];P38={111,28,39,412,510};gE38=ToGraph[E38,∞];ToGraph[E38,∞,EdgeStyleMap[#{Thick,Green}&,P38],GraphLayoutAutomatic,VertexCoordinatesOrthogon[7,7,1.5],VertexLabelsOrthogonLabels[7,7],ImagePadding10]

Out[]=

In[]:=

{DissectedGraphQ[gE38,X38],MaxPairingLength[gE38,X38]}

Out[]=

{True,7}

In[]:=

P38={111,28,39,412,510};AugmentingPath[E38,X38,Y38,P38,SelectionRuleLast,VertexCoordinatesOrthogon[1]]

Initial pairing:

{111,28,39,412,510}

Mx	x	xy	y	zy	z	Mz	FromWhere
{6,7}
{6}	7	711	11	111	1	{1}	{711,111}
{6}	7	710	10	510	5	{1,5}	{710,105}
{6}	7	79	9	39	3	{1,5,3}	{79,93}
{6}	7	78	8	28	2	{1,5,3,2}	{78,82}
∅	6	612	12	412	4	{1,5,3,2,4}	{612,124}
{1,5,3,2,4}
{1,5,3,2}	4	414	14			∅	{414}
∅

FromWhereList:

{711,111,710,510,79,39,78,28,612,412,414}

Augmenting Path:

{612,412,414}

Augmented Pairing:

{111,28,39,510,612,414}

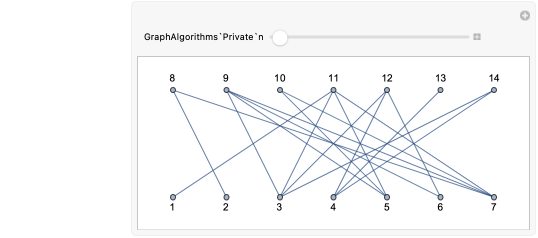
In[]:=

MaxPairing[ME38,X38,Y38,P38]

Initial pairing:

{111,28,39,412,510}

Mx	x	xy	y	zy	z	Mz	FromWhere
{6,7}
{7}	6	69	9	39	3	{3}	{69,93}
{7}	6	612	12	412	4	{3,4}	{612,124}
∅	7	78	8	28	2	{3,4,2}	{78,82}
∅	7	710	10	510	5	{3,4,2,5}	{710,105}
∅	7	711	11	111	1	{3,4,2,5,1}	{711,111}
{3,4,2,5,1}
{4,2,5,1}	3	314	14			∅	{314}
{2,5,1}	4	413	13			∅	{413}
∅

FromWhereList:

{69,93,612,124,78,82,710,105,711,111,314,413}

Augmenting Path:

{612,412,413}

Augmented Pairing:

{111,28,39,510,612,413}

***

Mx	x	xy	y	zy	z	Mz	FromWhere
{7}
∅	7	78	8	28	2	{2}	{78,82}
∅	7	79	9	39	3	{2,3}	{79,93}
∅	7	710	10	510	5	{2,3,5}	{710,105}
∅	7	711	11	111	1	{2,3,5,1}	{711,111}
{2,3,5,1}
{5,1}	3	312	12	612	6	{6}	{312,126}
{5,1}	3	314	14			{6}	{314}
∅

FromWhereList:

{78,82,79,93,710,105,711,111,312,126,314}

Augmenting Path:

{79,39,314}

Augmented Pairing:

{111,28,510,612,413,79,314}

***

The last pairing is maximal.

In[]:=

MaxPairingLength[ME38,X38]

Out[]=

Example 42: X = Range[1, 8], Y = Range[9, 16]

In[]:=

X39=Range[1,8];Y39=Range[9,16];E39={{1,9},{1,10},{1,12},{1,13},{2,10},{2,12},{3,9},{3,11},{3,13},{4,9},{4,12},{4,14},{4,15},{4,16},{5,13},{5,14},{5,15},{5,16},{6,9},{6,12},{7,10},{7,11},{8,10},{8,11}};P39={19,210,311,412,513};gE39=ToGraph[E39,∞];ToGraph[E39,∞,EdgeStyleMap[#{Thick,Green}&,P39],GraphLayoutAutomatic,VertexCoordinatesOrthogon[8,8,1],VertexLabelsOrthogonLabels[8,8],ImagePadding10]

Out[]=

In[]:=

{DissectedGraphQ[E39,X39,Y39],MaxPairingLength[E39,X39]}

Out[]=

{False,7}

In[]:=

AugmentingPath[gE39,X39,Y39,P39,SelectionRuleRandomChoice,VertexCoordinates"XY"]

Initial pairing:

{19,210,311,412,513}

Mx	x	xy	y	zy	z	Mz	FromWhere
{6,7,8}
{6,7}	8	810	10	210	2	{2}	{810,102}
{6,7}	8	811	11	311	3	{2,3}	{811,113}
∅	6	69	9	19	1	{2,3,1}	{69,91}
∅	6	612	12	412	4	{2,3,1,4}	{612,124}
{2,3,1,4}
{3,4}	1	113	13	513	5	{5}	{113,135}
{3}	4	414	14			{5}	{414}
∅

FromWhereList:

{810,210,811,311,69,19,612,412,113,513,414}

Augmenting Path:

{612,412,414}

Augmented Pairing:

{19,210,311,513,612,414}

In[]:=

P39={19,210,311,412,513};MaxPairing[E39,X39,Y39,P39,SelectionRuleRandomChoice,TraceReduce];

Initial pairing:

{19,210,311,412,513}

Mx	x	xy	y	zy	z	Mz	FromWhere
{6,7}	8	811	11	311	3	{3}	{811,113}
{6,7}	8	810	10	210	2	{3,2}	{810,102}
{7}	6	612	12	412	4	{3,2,4}	{612,124}
{7}	6	69	9	19	1	{3,2,4,1}	{69,91}
{2,4,1}	3	313	13	513	5	{5}	{313,135}
∅	4	415	15			{5}	{415}

FromWhereList:

{811,113,810,102,612,124,69,91,313,135,415}

Augmenting Path:

{612,412,415}

Augmented Pairing:

{19,210,311,513,612,415}

***

Mx	x	xy	y	zy	z	Mz	FromWhere
{7}	8	810	10	210	2	{2}	{810,102}
{7}	8	811	11	311	3	{2,3}	{811,113}
{2}	3	39	9	19	1	{1}	{39,91}
{2}	3	313	13	513	5	{1,5}	{313,135}
∅	2	212	12	612	6	{1,5,6}	{212,126}
{1,6}	5	514	14			∅	{514}

FromWhereList:

{810,102,811,113,39,91,313,135,212,126,514}

Augmenting Path:

{811,311,313,513,514}

Augmented Pairing:

{19,210,612,415,811,313,514}

***

Mx	x	xy	y	zy	z	Mz	FromWhere
∅	7	711	11	811	8	{8}	{711,118}
∅	7	710	10	210	2	{8,2}	{710,102}
{8}	2	212	12	612	6	{6}	{212,126}
∅	6	69	9	19	1	{1}	{69,91}
∅	1	113	13	313	3	{3}	{113,133}

FromWhereList:

{711,118,710,102,212,126,69,91,113,133}

There is no augmenting Path.

***

The last pairing is maximal

Example 43: X = Range[1, 7], Y = Range[8, 15]

In[]:=

X40=Range[1,7];Y40=Range[8,15];E40={{1,11},{2,9},{2,10},{3,8},{3,13},{4,9},{4,10},{4,14},{5,11},{5,12},{6,12},{6,14},{6,15},{7,10},{7,12}};P40={29,38,511,615,712};gE40=ToGraph[E40,∞];ToGraph[E40,∞,EdgeStyleMap[#{Thick,Green}&,P40],GraphLayoutAutomatic,VertexCoordinatesOrthogon[7,8,1],VertexLabelsOrthogonLabels[7,8],ImagePadding10]

Out[]=

In[]:=

{DissectedGraphQ[gE40,X40],MaxPairingLength[E40,X40]}

Out[]=

{True,7}

In[]:=

AugmentingPath[gE40,X40,Y40,P40,SelectionRuleRandomChoice,VertexCoordinates"XY"]

Initial pairing:

{29,38,511,615,712}

Extension of initial pairing found in a trivial way:

{29,38,511,615,712,410}

Mx	x	xy	y	zy	z	Mz	FromWhere
{1}
∅	1	111	11	511	5	{5}	{111,115}
{5}
∅	5	512	12	712	7	{7}	{512,127}
{7}
∅	7	710	10	410	4	{4}	{710,104}
{4}
∅	4	49	9	29	2	{2}	{49,92}
∅	4	414	14			{2}	{414}
∅

FromWhereList:

{111,511,512,712,710,410,49,29,414}

Augmenting Path:

{111,511,512,712,710,410,414}

Augmented Pairing:

{29,38,615,111,512,710,414}

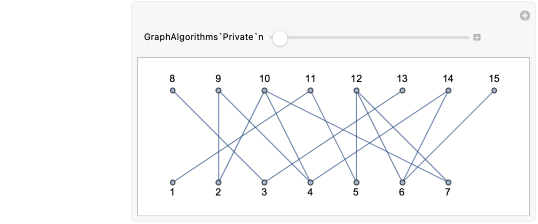
In[]:=

P40={29,38,511,712};MaxPairing[gE40,X40,Y40,P40,SelectionRuleRandomChoice,TraceReduce];

Initial pairing:

{29,38,511,712}

Extension of initial pairing found in a trivial way:

{29,38,511,712,410,614}

Mx	x	xy	y	zy	z	Mz	FromWhere
∅	1	111	11	511	5	{5}	{111,115}
∅	5	512	12	712	7	{7}	{512,127}
∅	7	710	10	410	4	{4}	{710,104}
∅	4	414	14	614	6	{6}	{414,146}
∅	4	49	9	29	2	{6,2}	{49,92}
∅	6	615	15			∅	{615}

FromWhereList:

{111,115,512,127,710,104,414,146,49,92,615}

Augmenting Path:

{111,511,512,712,710,410,414,614,615}

Augmented Pairing:

{29,38,111,512,710,414,615}

***

The last pairing is maximal.

Flows in Networks

Incrementing Path Algorithm

Alternatives for Incrementing Path Algorithm:-- Flow -> True | Essentialpart |False,-- FontSize -> 10 | any font size,-- ItemSize -> Automatic | List of numbers, -- Metod -> MaximalCapacity | ShortestPath,-- Print -> All | Last,-- SelectionRule  First | Last | RandomChoice,-- Spacings -> Automatic | {0.5, 0,8} | {number | Automatic, number | Automatic} | number,-- Trace -> True | Reduced | False.

In[]:=

Options[IncrementingPath]

Out[]=

{FlowTrue,FontSize10,FrameAll,ItemSizeAutomatic,MethodMaximalCapacity,PathTrue,SelectionRuleFirst,Spacings{1,0.5},TraceTrue}

Ford-Fulkerson Algorithm

Alternatives for optional arguments of FordFulkerson:-- Flow -> True | EssentialPart,-- FontSize -> 10 | any font size,-- ItemSize -> Automatic | List of numbers, -- Metod -> MaximalCapacity | ShortestPath,-- Print -> All | Last,-- SelectionRule  First | Last | RandomChoice,-- Spacings -> Automatic | {0.5, 0,8} | {number | Automatic, number | Automatic} | number,-- Trace -> True | Reduced | False.

In[]:=

Options[FordFulkerson]

Out[]=

{FlowTrue,FrameAll,FontSize10,ItemSizeAutomatic,MethodMaximalCapacity,PathTrue,SelectionRuleFirst,PrintAll,SpacingsAutomatic,TraceTrue}

Example 44

In[]:=

E41={{1,2},{1,3},{1,6},{2,3},{2,4},{3,4},{3,5},{4,5},{4,8},{5,1},{5,6},{5,7},{5,8},{6,9},{7,4},{7,9},{8,9}};ME41=ToWeightedAdjacencyMatrix[E41];gE41=ToGraph[E41];ToGraph[E41,AspectRatio1/3,GraphLayoutAutomatic,ImagePadding10,VertexLabels"Name"]

Out[]=

In[]:=

cfl41={{6,0,0},{6,2,0},{3,3,0},{2,0,0},{3,0,0},{4,0,0},{4,2,0},{5,4,3},{3,0,0},{3,1,1},{6,1,0},{5,4,0},{5,0,0},{5,4,0},{6,4,2},{3,0,0},{9,0,0}};c41=#[[1]]&/@cfl41;f41=#[[2]]&/@cfl41;l41=#[[3]]&/@cfl41;Ecfl41=MapThread[Join,{E41,cfl41}];Grid[Prepend[Ecfl41,{"Tail","Head","c","f","l"}]//Transpose,DividersAll,Spacings{1,0.5}]

Out[]=

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
c	6	6	3	2	3	4	4	5	3	3	6	5	5	5	6	3	9
f	0	2	3	0	0	0	2	4	0	1	1	4	0	4	4	0	0
l	0	0	0	0	0	0	0	3	0	1	0	0	0	0	2	0	0

In[]:=

{NetworkQ[gE41,c41,l41],FlowQ[E41,{1,9},f41],FlowValue[E41,{1,9},f41]}

Out[]=

{True,True,4}

In[]:=

IncrementingPath[gE41,c41,l41,{1,9},f41,FontSize10,MethodMaximalCapacity,SelectionRuleFirst,TraceTrue]

f-incrementing path with capacity 3:

{{{1,3},1},{{3,4},1},{{4,8},1},{{8,9},1}}

Incremented flow f with value 7;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	0	5	3	0	0	3	2	4	3	1	1	4	0	4	4	0	3

x	M	y	δ(x)	δ(e)	δ(y)	FromWhere(y)	M
							{1}
1	∅	2	∞	6	6	{{1,2},1}	{2}
-∥-	{2}	3	∞	4	4	{{1,3},1}	{2,3}
-∥-	{2,3}	6	∞	0	0		{2,3}
-∥-	-∥-	5	∞	0	0		{2,3}
2	{3}	3	6	2	4		{3}
-∥-	-∥-	4	6	3	3	{{2,4},1}	{3,4}
3	{4}	4	4	4	4	{{3,4},1}	{4}
-∥-	-∥-	5	4	2	2	{{3,5},1}	{4,5}
4	{5}	5	4	1	2		{5}
-∥-	-∥-	8	4	3	3	{{4,8},1}	{5,8}
-∥-	{5,8}	7	4	2	2	{{7,4},-1}	{5,8,7}
5	{8,7}	6	2	5	2	{{5,6},1}	{8,7,6}
-∥-	{8,7,6}	7	2	1	2		{8,7,6}
-∥-	-∥-	8	2	5	3		{8,7,6}
8	{7,6}	9	3	9	3	{{8,9},1}	{7,6,9}

★★★

In[]:=

IncrementingPath[E41,c41,l41,{1,9},f41,FlowTrue,FontSize10,MethodShortestPath,SelectionRuleLast,TraceTrue]

f-incrementing path with capacity 2:

{{{1,3},1},{{3,5},1},{{5,8},1},{{8,9},1}}

Incremented flow f with value 6;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	0	4	3	0	0	0	4	4	0	1	1	4	2	4	4	0	2

x	M	y	δ(x)	δ(e)	δ(y)	FromWhere(y)	M
							{1}
1	∅	5	∞	0	0		∅
-∥-	-∥-	6	∞	0	0		∅
-∥-	-∥-	3	∞	4	4	{{1,3},1}	{3}
-∥-	{3}	2	∞	6	6	{{1,2},1}	{3,2}
3	{2}	2	4	0	6		{2}
-∥-	-∥-	5	4	2	2	{{3,5},1}	{2,5}
-∥-	{2,5}	4	4	4	4	{{3,4},1}	{2,5,4}
2	{5,4}	4	6	3	4		{5,4}
5	{4}	4	2	1	4		{4}
-∥-	-∥-	8	2	5	2	{{5,8},1}	{4,8}
-∥-	{4,8}	7	2	1	1	{{5,7},1}	{4,8,7}
-∥-	{4,8,7}	6	2	5	2	{{5,6},1}	{4,8,7,6}
4	{8,7,6}	7	4	2	1		{8,7,6}
-∥-	-∥-	8	4	3	2		{8,7,6}
8	{7,6}	9	2	9	2	{{8,9},1}	{7,6,9}

★★★

In[]:=

FordFulkerson[gE41,c41,l41,{1,9},f41,PrintLast,MethodMaximalCapacity,PathFalse,SelectionRuleFirst,TraceReduce]

Incremented flow f with value 12;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	4	6	3	1	3	3	4	5	3	1	2	5	1	5	2	3	4

★★★

There is no f-incrementing path.

x	M	y	δ(x)	δ(e)	δ(y)	FromWhere(y)	M
							{1}
1	∅	2	∞	2	2	{{1,2},1}	{2}
2	∅	3	2	1	1	{{2,3},1}	{3}
3	∅	4	1	1	1	{{3,4},1}	{4}

The last flow with value 12 is maximal

★★★

In[]:=

FordFulkerson[gE41,c41,l41,{1,9},f41,PrintAll,MethodMaximalCapacity,SelectionRuleRandomChoice,TraceFalse]

f-incrementing path with capacity 3:

{{{1,3},1},{{3,4},1},{{4,8},1},{{8,9},1}}

Incremented flow f with value 7;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	0	5	3	0	0	3	2	4	3	1	1	4	0	4	4	0	3

★★★

f-incrementing path with capacity 1:

{{{1,3},1},{{3,5},1},{{5,6},1},{{6,9},1}}

Incremented flow f with value 8;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	0	6	3	0	0	3	3	4	3	1	2	4	0	5	4	0	3

★★★

f-incrementing path with capacity 2:

{{{1,2},1},{{2,4},1},{{7,4},-1},{{7,9},1}}

Incremented flow f with value 10;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	2	6	3	0	2	3	3	4	3	1	2	4	0	5	2	2	3

★★★

f-incrementing path with capacity 1:

{{{1,2},1},{{2,3},1},{{3,5},1},{{5,8},1},{{8,9},1}}

Incremented flow f with value 11;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	3	6	3	1	2	3	4	4	3	1	2	4	1	5	2	2	4

★★★

f-incrementing path with capacity 1:

{{{1,2},1},{{2,4},1},{{4,5},1},{{5,8},1},{{8,9},1}}

Incremented flow f with value 12;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	4	6	3	1	3	3	4	5	3	1	2	4	2	5	2	2	5

★★★

There is no f-incrementing path

The last flow with value 12 is maximal.

★★★

In[]:=

FordFulkerson[gE41,c41,l41,{1,9},f41,PrintLast,MethodShortestPath,SelectionRuleFirst,TraceFalse]

Incremented flow f with value 12;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	4	6	3	1	3	3	4	5	3	1	2	5	1	5	2	3	4

★★★

There is no f-incrementing path.

The last flow with value 12 is maximal

★★★

In[]:=

FordFulkerson[gE41,c41,l41,{1,9},f41,PrintAll,MethodMaximalCapacity,SelectionRuleFirst,TraceFalse]

f-incrementing path with capacity 3:

{{{1,3},1},{{3,4},1},{{4,8},1},{{8,9},1}}

Incremented flow f with value 7;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	0	5	3	0	0	3	2	4	3	1	1	4	0	4	4	0	3

★★★

f-incrementing path with capacity 2:

{{{1,2},1},{{2,4},1},{{7,4},-1},{{7,9},1}}

Incremented flow f with value 9;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	2	5	3	0	2	3	2	4	3	1	1	4	0	4	2	2	3

★★★

f-incrementing path with capacity 1:

{{{1,2},1},{{2,3},1},{{3,5},1},{{5,6},1},{{6,9},1}}

Incremented flow f with value 10;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	3	5	3	1	2	3	3	4	3	1	2	4	0	5	2	2	3

★★★

f-incrementing path with capacity 1:

{{{1,3},1},{{3,5},1},{{5,7},1},{{7,9},1}}

Incremented flow f with value 11;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	3	6	3	1	2	3	4	4	3	1	2	5	0	5	2	3	3

★★★

f-incrementing path with capacity 1:

{{{1,2},1},{{2,4},1},{{4,5},1},{{5,8},1},{{8,9},1}}

Incremented flow f with value 12;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	4	6	3	1	3	3	4	5	3	1	2	5	1	5	2	3	4

★★★

There is no f-incrementing path

The last flow with value 12 is maximal.

★★★

In[]:=

FordFulkerson[gE41,c41,l41,{1,9},f41,PrintAll,MethodShortestPath,SelectionRuleFirst,TraceFalse]

f-incrementing path with capacity 3:

{{{1,2},1},{{2,4},1},{{4,8},1},{{8,9},1}}

Incremented flow f with value 7;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	3	2	3	0	3	0	2	4	3	1	1	4	0	4	4	0	3

★★★

f-incrementing path with capacity 2:

{{{1,3},1},{{3,4},1},{{7,4},-1},{{7,9},1}}

Incremented flow f with value 9;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	3	4	3	0	3	2	2	4	3	1	1	4	0	4	2	2	3

★★★

f-incrementing path with capacity 1:

{{{1,3},1},{{3,5},1},{{5,6},1},{{6,9},1}}

Incremented flow f with value 10;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	3	5	3	0	3	2	3	4	3	1	2	4	0	5	2	2	3

★★★

f-incrementing path with capacity 1:

{{{1,3},1},{{3,5},1},{{5,7},1},{{7,9},1}}

Incremented flow f with value 11;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	3	6	3	0	3	2	4	4	3	1	2	5	0	5	2	3	3

★★★

f-incrementing path with capacity 1:

{{{1,2},1},{{2,3},1},{{3,4},1},{{4,5},1},{{5,8},1},{{8,9},1}}

Incremented flow f with value 12;

Tail	1	1	1	2	2	3	3	4	4	5	5	5	5	6	7	7	8
Head	2	3	6	3	4	4	5	5	8	1	6	7	8	9	4	9	9
f	4	6	3	1	3	3	4	5	3	1	2	5	1	5	2	3	4

★★★

There is no f-incrementing path

The last flow with value 12 is maximal.

★★★

Example 45

In[]:=

E42={{1,2},{1,3},{1,6},{2,3},{2,4},{3,4},{3,5},{4,5},{8,4},{5,1},{5,6},{5,7},{5,8},{6,8},{7,4},{9,7},{9,8}};gE42=Graph[E42,DirectedEdgesTrue,ImagePadding10,VertexLabels"Name"]

Out[]=

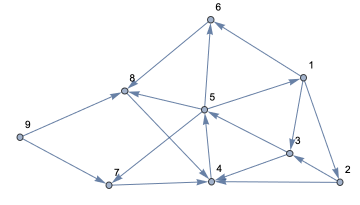
In[]:=

cfl42={{6,0,0},{6,0,0},{4,0,0},{2,0,0},{3,0,0},{4,0,0},{4,0,0},{5,4,3},{3,0,0},{3,0,0},{6,0,0},{5,4,0},{5,0,0},{5,0,0},{6,4,2},{3,0,0},{9,0,0}};c42=#[[1]]&/@cfl42;f42=#[[2]]&/@cfl42;l42=#[[3]]&/@cfl42;Ecfl42=MapThread[Join,{E42,cfl42}];Grid[Prepend[Ecfl42,{"Tail","Head","c","f","l"}]//Transpose,DividersAll]

Out[]=

Tail	1	1	1	2	2	3	3	4	8	5	5	5	5	6	7	9	9
Head	2	3	6	3	4	4	5	5	4	1	6	7	8	8	4	7	8
c	6	6	4	2	3	4	4	5	3	3	6	5	5	5	6	3	9
f	0	0	0	0	0	0	0	4	0	0	0	4	0	0	4	0	0
l	0	0	0	0	0	0	0	3	0	0	0	0	0	0	2	0	0

In[]:=

{NetworkQ[gE42,c42,l42],FlowQ[E42,{1,9},f42],FlowValue[E42,{1,9},f42]}

Out[]=

{True,True,0}

In[]:=

IncrementingPath[gE42,c42,l42,{1,9},f42,FlowTrue,FontSize10,MethodMaximalCapacity,PathTrue,SelectionRuleFirst,TraceTrue]

There is no f-incrementing path

x	M	y	δ(x)	δ(e)	δ(y)	FromWhere(y)	M
							{1}
1	∅	2	∞	6	6	{{1,2},1}	{2}
-∥-	{2}	3	∞	6	6	{{1,3},1}	{2,3}
-∥-	{2,3}	6	∞	4	4	{{1,6},1}	{2,3,6}
-∥-	{2,3,6}	5	∞	0	0		{2,3,6}
2	{3,6}	3	6	2	6		{3,6}
-∥-	-∥-	4	6	3	3	{{2,4},1}	{3,6,4}
3	{6,4}	4	6	4	4	{{3,4},1}	{6,4}
-∥-	-∥-	5	6	4	4	{{3,5},1}	{6,4,5}
6	{4,5}	8	4	5	4	{{6,8},1}	{4,5,8}
-∥-	{4,5,8}	5	4	0	4		{4,5,8}
4	{5,8}	5	4	1	4		{5,8}
-∥-	-∥-	8	4	0	4		{5,8}
-∥-	-∥-	7	4	2	2	{{7,4},-1}	{5,8,7}
5	{8,7}	7	4	1	2		{8,7}
-∥-	-∥-	8	4	5	4		{8,7}
8	{7}	9	4	0	0		{7}
7	∅	9	2	0	0		∅

★★★

In[]:=

FordFulkerson[gE42,c42,l42,{1,9},f42,PrintLast,TraceReduce,MethodShortestPath]

Incremented flow f with value GraphAlgorithms`Private`value$13506;

GraphAlgorithms`Private`ef$13506

★★★

There is no f-incrementing path.

x	M	y	δ(x)	δ(e)	δ(y)	FromWhere(y)	M
							{1}
1	∅	2	∞	6	6	{{1,2},1}	{2}
-∥-	{2}	3	∞	6	6	{{1,3},1}	{2,3}
-∥-	{2,3}	6	∞	4	4	{{1,6},1}	{2,3,6}
-∥-	-∥-	4	6	3	3	{{2,4},1}	{3,6,4}
-∥-	-∥-	5	6	4	4	{{3,5},1}	{6,4,5}
6	{4,5}	8	4	5	4	{{6,8},1}	{4,5,8}
-∥-	-∥-	7	3	2	2	{{7,4},-1}	{5,8,7}

The last flow with value GraphAlgorithms`Private`value$13506 is maximal

★★★

Example 46

In[]:=

E43={{1,7},{1,11},{2,3},{2,8},{2,11},{3,4},{3,8},{3,13},{4,5},{4,10},{4,13},{4,14},{5,6},{5,10},{7,2},{7,3},{7,8},{8,4},{8,9},{9,4},{9,5},{9,10},{10,6},{11,3},{11,12},{12,3},{12,4},{12,13},{13,14},{14,5},{14,6}};gE43=Graph[E43,DirectedEdgesTrue,GraphLayout"SpringEmbedding",ImagePadding10,VertexLabels"Name"]

Out[]=

In[]:=

c43={2,1,1,2,1,1,1,2,1,2,1,2,2,1,1,1,2,1,1,1,1,1,2,2,1,1,2,1,1,1,2};f43=l43=0*Range[Length@E43];cfl43=Thread[List[c43,f43,l43]];Ecfl43=MapThread[Join,{E43,cfl43}];StylePrint/@{Grid[Transpose[Join[{{"Tail","Head","c","f","l"}},Ecfl43[[;;16]]]],FrameAll],Grid[Transpose[Join[{{"Tail","Head","c","f","l"}},Ecfl43[[17;;]]]],FrameAll]};

Tail	1	1	2	2	2	3	3	3	4	4	4	4	5	5	7	7
Head	7	11	3	8	11	4	8	13	5	10	13	14	6	10	2	3
c	2	1	1	2	1	1	1	2	1	2	1	2	2	1	1	1
f	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
l	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Tail	7	8	8	9	9	9	10	11	11	12	12	12	13	14	14
Head	8	4	9	4	5	10	6	3	12	3	4	13	14	5	6
c	2	1	1	1	1	1	2	2	1	1	2	1	1	1	2
f	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
l	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

In[]:=

{NetworkQ[gE43,c43,l43],FlowQ[E43,{1,9},f43],FlowValue[E43,{1,9},f43]}

Out[]=

{True,True,0}

In[]:=

IncrementingPath[gE43,c43,l43,{1,6},f43,FlowEssentialPart,FontSize10,PathTrue,MethodShortestPath,PathTrue,SelectionRuleRandomChoice,TraceReduce]

f-incrementing path with capacity 1:

{{{1,11},1},{{11,3},1},{{3,13},1},{{13,14},1},{{14,6},1}}

Incremented flow f with value 1;

Tail	1	3	11	13	14
Head	11	13	3	14	6
f	1	1	1	1	1

x	M	y	δ(x)	δ(e)	δ(y)	FromWhere(y)	M
							{1}
1	∅	11	∞	1	1	{{1,11},1}	{11}
-∥-	{11}	7	∞	2	2	{{1,7},1}	{11,7}
11	{7}	3	1	2	1	{{11,3},1}	{7,3}
-∥-	-∥-	12	1	1	1	{{11,12},1}	{7,3,12}
7	{3,12}	2	2	1	1	{{7,2},1}	{3,12,2}
-∥-	-∥-	8	2	2	2	{{7,8},1}	{3,12,2,8}
3	{12,2,8}	13	1	2	1	{{3,13},1}	{12,2,8,13}
-∥-	-∥-	4	1	1	1	{{3,4},1}	{12,2,8,13,4}
8	{13,4}	9	2	1	1	{{8,9},1}	{13,4,9}
-∥-	-∥-	14	1	1	1	{{13,14},1}	{4,9,14}
4	{9,14}	5	1	1	1	{{4,5},1}	{9,14,5}
-∥-	-∥-	10	1	2	1	{{4,10},1}	{9,14,5,10}
14	{5,10}	6	1	2	1	{{14,6},1}	{5,10,6}

★★★

In[]:=

IncrementingPath[gE43,c43,l43,{1,6},f43,FlowEssentialPart,FontSize10,PathTrue,MethodMaximalCapacity,SelectionRuleRandomChoice,TraceTrue]

f-incrementing path with capacity 1:

{{{1,7},1},{{7,3},1},{{3,13},1},{{13,14},1},{{14,6},1}}

Incremented flow f with value 1;

Tail	1	3	7	13	14
Head	7	13	3	14	6
f	1	1	1	1	1

x	M	y	δ(x)	δ(e)	δ(y)	FromWhere(y)	M
							{1}
1	∅	7	∞	2	2	{{1,7},1}	{7}
-∥-	{7}	11	∞	1	1	{{1,11},1}	{7,11}
7	{11}	3	2	1	1	{{7,3},1}	{11,3}
-∥-	{11,3}	8	2	2	2	{{7,8},1}	{11,3,8}
-∥-	{11,3,8}	2	2	1	1	{{7,2},1}	{11,3,8,2}
11	{3,8,2}	2	1	0	1		{3,8,2}
-∥-	-∥-	12	1	1	1	{{11,12},1}	{3,8,2,12}
-∥-	{3,8,2,12}	3	1	2	1		{3,8,2,12}
3	{8,2,12}	13	1	2	1	{{3,13},1}	{8,2,12,13}
-∥-	{8,2,12,13}	2	1	0	1		{8,2,12,13}
-∥-	-∥-	12	1	0	1		{8,2,12,13}
-∥-	-∥-	8	1	1	2		{8,2,12,13}
-∥-	-∥-	4	1	1	1	{{3,4},1}	{8,2,12,13,4}
8	{2,12,13,4}	2	2	0	1		{2,12,13,4}
-∥-	-∥-	4	2	1	1		{2,12,13,4}
-∥-	-∥-	9	2	1	1	{{8,9},1}	{2,12,13,4,9}
12	{13,4,9}	13	1	1	1		{13,4,9}
-∥-	-∥-	4	1	2	1		{13,4,9}
13	{4,9}	4	1	0	1		{4,9}
-∥-	-∥-	14	1	1	1	{{13,14},1}	{4,9,14}
4	{9,14}	10	1	2	1	{{4,10},1}	{9,14,10}
-∥-	{9,14,10}	5	1	1	1	{{4,5},1}	{9,14,10,5}
-∥-	{9,14,10,5}	9	1	0	1		{9,14,10,5}
-∥-	-∥-	14	1	2	1		{9,14,10,5}
9	{14,10,5}	5	1	1	1		{14,10,5}
-∥-	-∥-	10	1	1	1		{14,10,5}
14	{10,5}	5	1	1	1		{10,5}
-∥-	-∥-	6	1	2	1	{{14,6},1}	{10,5,6}

★★★

In[]:=

FordFulkerson[gE43,c43,{1,6},f43,FlowEssentialPart,MethodMaximalCapacity,PrintAll,SelectionRuleRandomChoice,TraceReduce]

f-incrementing path with capacity 1:

{{{1,7},1},{{7,8},1},{{8,9},1},{{9,10},1},{{10,6},1}}

Incremented flow f with value 1;

Tail	1	7	8	9	10
Head	7	8	9	10	6
f	1	1	1	1	1

x	M	y	δ(x)	δ(e)	δ(y)	FromWhere(y)	M
							{1}
1	∅	7	∞	2	2	{{1,7},1}	{7}
-∥-	{7}	11	∞	1	1	{{1,11},1}	{7,11}
7	{11}	2	2	1	1	{{7,2},1}	{11,2}
-∥-	{11,2}	8	2	2	2	{{7,8},1}	{11,2,8}
-∥-	{11,2,8}	3	2	1	1	{{7,3},1}	{11,2,8,3}
-∥-	-∥-	12	1	1	1	{{11,12},1}	{2,8,3,12}
-∥-	-∥-	9	2	1	1	{{8,9},1}	{3,12,9}
-∥-	{3,12,9}	4	2	1	1	{{8,4},1}	{3,12,9,4}
-∥-	-∥-	13	1	2	1	{{3,13},1}	{12,9,4,13}
-∥-	-∥-	10	1	1	1	{{9,10},1}	{4,13,10}
-∥-	{4,13,10}	5	1	1	1	{{9,5},1}	{4,13,10,5}
-∥-	-∥-	14	1	2	1	{{4,14},1}	{13,10,5,14}
-∥-	-∥-	6	1	2	1	{{10,6},1}	{5,14,6}

★★★

f-incrementing path with capacity 1:

{{{1,11},1},{{11,3},1},{{3,13},1},{{13,14},1},{{14,6},1}}

Incremented flow f with value 2;

Tail	1	1	3	7	8	9	10	11	13	14
Head	7	11	13	8	9	10	6	3	14	6
f	1	1	1	1	1	1	1	1	1	1

x	M	y	δ(x)	δ(e)	δ(y)	FromWhere(y)	M
							{1}
1	∅	11	∞	1	1	{{1,11},1}	{11}
-∥-	{11}	7	∞	1	1	{{1,7},1}	{11,7}
-∥-	-∥-	3	1	2	1	{{11,3},1}	{7,3}
-∥-	{7,3}	12	1	1	1	{{11,12},1}	{7,3,12}
7	{3,12}	2	1	1	1	{{7,2},1}	{3,12,2}
-∥-	-∥-	8	1	1	1	{{7,8},1}	{3,12,2,8}
-∥-	-∥-	13	1	2	1	{{3,13},1}	{12,2,8,13}
-∥-	{12,2,8,13}	4	1	1	1	{{3,4},1}	{12,2,8,13,4}
-∥-	-∥-	14	1	1	1	{{13,14},1}	{4,14}
4	{14}	10	1	2	1	{{4,10},1}	{14,10}
-∥-	-∥-	5	1	1	1	{{4,5},1}	{14,10,5}
-∥-	-∥-	6	1	2	1	{{14,6},1}	{10,5,6}

★★★

f-incrementing path with capacity 1:

{{{1,7},1},{{7,8},1},{{8,4},1},{{4,10},1},{{10,6},1}}

Incremented flow f with value 3;

Tail	1	1	3	4	7	8	8	9	10	11	13	14
Head	7	11	13	10	8	4	9	10	6	3	14	6
f	2	1	1	1	2	1	1	1	2	1	1	1

x	M	y	δ(x)	δ(e)	δ(y)	FromWhere(y)	M
							{1}
1	∅	7	∞	1	1	{{1,7},1}	{7}
7	∅	8	1	1	1	{{7,8},1}	{8}
-∥-	{8}	2	1	1	1	{{7,2},1}	{8,2}
-∥-	{8,2}	3	1	1	1	{{7,3},1}	{8,2,3}
-∥-	-∥-	4	1	1	1	{{8,4},1}	{2,3,4}
-∥-	-∥-	11	1	1	1	{{2,11},1}	{3,4,11}
3	{4,11}	13	1	1	1	{{3,13},1}	{4,11,13}
-∥-	-∥-	10	1	2	1	{{4,10},1}	{11,13,10}
-∥-	-∥-	14	1	2	1	{{4,14},1}	{11,13,10,14}
-∥-	{11,13,10,14}	5	1	1	1	{{4,5},1}	{11,13,10,14,5}
11	{13,10,14,5}	12	1	1	1	{{11,12},1}	{13,10,14,5,12}
10	{14,5,12}	6	1	1	1	{{10,6},1}	{14,5,12,6}

★★★

There is no f-incrementing path

x	M	y	δ(x)	δ(e)	δ(y)	FromWhere(y)	M
							{1}
10	{14,5,12}	6	1	1	1	{{10,6},1}	{14,5,12,6}

The last flow with value 3 is maximal.

★★★

Definitions



Cite this as: Vojtěch (Vojtech) Bartík (Bartik), "Graph algorithms" from the Notebook Archive (2021), https://notebookarchive.org/2021-11-a6bkcrc

∞	8	2	2	9	2
8	∞	-5	-1	∞	19
2	-5	∞	-5	3	14
2	-1	-5	∞	3	-2
9	∞	3	3	∞	2
2	19	14	-2	2	∞

∞	2	2	3	2	-4	2
2	∞	∞	2	∞	3	1
2	∞	∞	-3	4	1	∞
3	2	-3	∞	1	2	4
2	∞	4	1	∞	2	∞
-4	3	1	2	2	∞	1
2	1	∞	4	∞	1	∞

∞	1	-2	4	-1	2	3
1	∞	∞	-2	4	∞	-4
-2	∞	∞	1	3	2	-2
4	-2	1	∞	-3	-2	-1
-1	4	3	-3	∞	1	4
2	∞	2	-2	1	∞	-3
3	-4	-2	-1	4	-3	∞

∞	-1	∞	-2	4	3	1	∞
-1	∞	∞	∞	4	-1	3	-1
∞	∞	∞	-3	∞	3	2	∞
-2	∞	-3	∞	∞	∞	3	3
4	4	∞	∞	∞	-4	-1	2
3	-1	3	∞	-4	∞	4	4
1	3	2	3	-1	4	∞	-4
∞	-1	∞	3	2	4	-4	∞

∞	∞	-3	3	∞	∞	2	4
∞	∞	2	-3	2	4	∞	3
-3	2	∞	2	-2	-1	4	∞
3	-3	2	∞	∞	∞	∞	3
∞	2	-2	∞	∞	∞	-1	∞
∞	4	-1	∞	∞	∞	3	-2
2	∞	4	∞	-1	3	∞	∞
4	3	∞	3	∞	-2	∞	∞

∞	∞	-2	1	-1	1	∞	-1	1	∞
∞	∞	2	4	∞	∞	∞	∞	∞	-4
-2	2	∞	∞	∞	∞	∞	∞	2	∞
1	4	∞	∞	-3	-3	-2	∞	∞	3
-1	∞	∞	-3	∞	∞	∞	∞	1	∞
1	∞	∞	-3	∞	∞	∞	∞	∞	-4
∞	∞	∞	-2	∞	∞	∞	-3	-4	3
-1	∞	∞	∞	∞	∞	-3	∞	∞	∞
1	∞	2	∞	1	∞	-4	∞	∞	3
∞	-4	∞	3	∞	-4	3	∞	3	∞

∞	3	∞	-2	7	2	∞	9	∞	∞
3	∞	-2	∞	∞	3	8	5	2	∞
∞	-2	∞	∞	∞	4	∞	-2	1	∞
-2	∞	∞	∞	9	1	2	∞	7	3
7	∞	∞	9	∞	∞	-2	∞	∞	-1
2	3	4	1	∞	∞	∞	6	∞	6
∞	8	∞	2	-2	∞	∞	∞	3	∞
9	5	-2	∞	∞	6	∞	∞	1	∞
∞	2	1	7	∞	∞	3	1	∞	9
∞	∞	∞	3	-1	6	∞	∞	9	∞

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	1	∞
-4	∞	0	∞	∞	∞	∞	∞	∞
∞	∞	3	0	∞	4	∞	12	∞
8	17	∞	10	0	∞	∞	∞	∞
∞	12	12	∞	∞	0	10	∞	∞
∞	∞	∞	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	4	∞	∞	0

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	∞	∞
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	∞
10	10	∞	10	0	∞	∞	∞	∞
∞	12	∞	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	∞	∞	-7	0

x	1	1	2	3	4	4	4	5	5	5	6	6	6	7	8	8	9
y	2	6	3	9	3	6	8	1	2	4	2	7	9	9	2	7	8
w	2	12	1	5	-3	4	2	10	10	10	12	10	-5	1	1	7	-7

∞	8	2	2	9	2
8	∞	-5	-1	∞	19
2	-5	∞	-5	3	14
2	-1	-5	∞	3	-2
9	∞	3	3	∞	2
2	19	14	-2	2	∞

∞	2	2	3	2	-4	2
2	∞	∞	2	∞	3	1
2	∞	∞	-3	4	1	∞
3	2	-3	∞	1	2	4
2	∞	4	1	∞	2	∞
-4	3	1	2	2	∞	1
2	1	∞	4	∞	1	∞

∞	1	-2	4	-1	2	3
1	∞	∞	-2	4	∞	-4
-2	∞	∞	1	3	2	-2
4	-2	1	∞	-3	-2	-1
-1	4	3	-3	∞	1	4
2	∞	2	-2	1	∞	-3
3	-4	-2	-1	4	-3	∞

∞	-1	∞	-2	4	3	1	∞
-1	∞	∞	∞	4	-1	3	-1
∞	∞	∞	-3	∞	3	2	∞
-2	∞	-3	∞	∞	∞	3	3
4	4	∞	∞	∞	-4	-1	2
3	-1	3	∞	-4	∞	4	4
1	3	2	3	-1	4	∞	-4
∞	-1	∞	3	2	4	-4	∞

∞	∞	-3	3	∞	∞	2	4
∞	∞	2	-3	2	4	∞	3
-3	2	∞	2	-2	-1	4	∞
3	-3	2	∞	∞	∞	∞	3
∞	2	-2	∞	∞	∞	-1	∞
∞	4	-1	∞	∞	∞	3	-2
2	∞	4	∞	-1	3	∞	∞
4	3	∞	3	∞	-2	∞	∞

∞	∞	-2	1	-1	1	∞	-1	1	∞
∞	∞	2	4	∞	∞	∞	∞	∞	-4
-2	2	∞	∞	∞	∞	∞	∞	2	∞
1	4	∞	∞	-3	-3	-2	∞	∞	3
-1	∞	∞	-3	∞	∞	∞	∞	1	∞
1	∞	∞	-3	∞	∞	∞	∞	∞	-4
∞	∞	∞	-2	∞	∞	∞	-3	-4	3
-1	∞	∞	∞	∞	∞	-3	∞	∞	∞
1	∞	2	∞	1	∞	-4	∞	∞	3
∞	-4	∞	3	∞	-4	3	∞	3	∞

∞	3	∞	-2	7	2	∞	9	∞	∞
3	∞	-2	∞	∞	3	8	5	2	∞
∞	-2	∞	∞	∞	4	∞	-2	1	∞
-2	∞	∞	∞	9	1	2	∞	7	3
7	∞	∞	9	∞	∞	-2	∞	∞	-1
2	3	4	1	∞	∞	∞	6	∞	6
∞	8	∞	2	-2	∞	∞	∞	3	∞
9	5	-2	∞	∞	6	∞	∞	1	∞
∞	2	1	7	∞	∞	3	1	∞	9
∞	∞	∞	3	-1	6	∞	∞	9	∞

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	1	∞
-4	∞	0	∞	∞	∞	∞	∞	∞
∞	∞	3	0	∞	4	∞	12	∞
8	17	∞	10	0	∞	∞	∞	∞
∞	12	12	∞	∞	0	10	∞	∞
∞	∞	∞	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	4	∞	∞	0

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	∞	∞
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	∞
10	10	∞	10	0	∞	∞	∞	∞
∞	12	∞	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	∞	∞	-7	0

x	1	1	2	3	4	4	4	5	5	5	6	6	6	7	8	8	9
y	2	6	3	9	3	6	8	1	2	4	2	7	9	9	2	7	8
w	2	12	1	5	-3	4	2	10	10	10	12	10	-5	1	1	7	-7

Graph Algorithms

Axiliary Definitions

EdgeListQ[E] returns True if E may be considered as the EdgeList of a directed or undirected graph in the sense of Mathematica, and False in the opposite case.​EdgeListQ[E,∞] returns True if Graph[E] is undirected graph in the sense of Mathematica and False in the opposite case.

ToEdgeList

ToWeightedEdgeList

ToWeightedAdjacencyMatrix

ToGraph

ToEdgeWeightedGraph

Random EdgeLists, Matrices and Graphs

RandomEdgeList, RandomWeightedEdgeList

RandomWeightedAdjacencyMatrix

RandomAcyclicGraph

Components

Example 1

Example 2

Minimal Spanning Tree

Options

Example 3

Example 4

Example 5

Example 6

Example 7

Example 8

Example 9

Strong Components, Condensation and Tarjan’s algorithm

Options

Example 10

Example 11

Example 12

Example 13

Example 14

Example 15

Topological Order, TopologicalOrderTest

Options

Example 16

Example 17

Example 18

Example 19

Example 20

Example 21

Shortest Paths: DijkstraPathsTree

Options

Example 22

Example 23

Example 24

Example 25

Example 26

Example 27

Shortest Paths: Floyd’s Algorithm

Options

Example 22

Example 23

Example 24

Example 25

Example 26

Example 27

Shortest Paths: FloydShortestPaths

Options

Example 28

Example 29

Example 30

Example 31

Example 32

Example 33

EulerTourQ and EulerTour

Example 34

Example 35

Example 36

Example 37

Example 38

Pairing in Bipartite (Dissected) Graphs

AugmentingPath

MaxPairing

Example 39: X = Range[1, 7], Y = Range[8, 15]

Example 40: X = Range[1, 7], Y = Range[8, 15]

Example 41: X = Range[1, 7], Y = Range[8, 14]

Example 42: X = Range[1, 8], Y = Range[9, 16]

Example 43: X = Range[1, 7], Y = Range[8, 15]

Flows in Networks

Incrementing Path Algorithm

EdgeListQ[E]
returns True if
E
may be considered as the EdgeList of a directed or undirected graph in the sense of Mathematica, and False in the opposite case.
EdgeListQ[E,∞]
returns True if
Graph[E]
is undirected graph in the sense of Mathematica and False in the opposite case.


ToEdgeList


ToWeightedEdgeList


ToWeightedAdjacencyMatrix


ToGraph


ToEdgeWeightedGraph


RandomEdgeList, RandomWeightedEdgeList


RandomWeightedAdjacencyMatrix


RandomAcyclicGraph


∞	8	2	2	9	2
8	∞	-5	-1	∞	19
2	-5	∞	-5	3	14
2	-1	-5	∞	3	-2
9	∞	3	3	∞	2
2	19	14	-2	2	∞

∞	2	2	3	2	-4	2
2	∞	∞	2	∞	3	1
2	∞	∞	-3	4	1	∞
3	2	-3	∞	1	2	4
2	∞	4	1	∞	2	∞
-4	3	1	2	2	∞	1
2	1	∞	4	∞	1	∞

∞	1	-2	4	-1	2	3
1	∞	∞	-2	4	∞	-4
-2	∞	∞	1	3	2	-2
4	-2	1	∞	-3	-2	-1
-1	4	3	-3	∞	1	4
2	∞	2	-2	1	∞	-3
3	-4	-2	-1	4	-3	∞

∞	-1	∞	-2	4	3	1	∞
-1	∞	∞	∞	4	-1	3	-1
∞	∞	∞	-3	∞	3	2	∞
-2	∞	-3	∞	∞	∞	3	3
4	4	∞	∞	∞	-4	-1	2
3	-1	3	∞	-4	∞	4	4
1	3	2	3	-1	4	∞	-4
∞	-1	∞	3	2	4	-4	∞

∞	∞	-3	3	∞	∞	2	4
∞	∞	2	-3	2	4	∞	3
-3	2	∞	2	-2	-1	4	∞
3	-3	2	∞	∞	∞	∞	3
∞	2	-2	∞	∞	∞	-1	∞
∞	4	-1	∞	∞	∞	3	-2
2	∞	4	∞	-1	3	∞	∞
4	3	∞	3	∞	-2	∞	∞

∞	∞	-2	1	-1	1	∞	-1	1	∞
∞	∞	2	4	∞	∞	∞	∞	∞	-4
-2	2	∞	∞	∞	∞	∞	∞	2	∞
1	4	∞	∞	-3	-3	-2	∞	∞	3
-1	∞	∞	-3	∞	∞	∞	∞	1	∞
1	∞	∞	-3	∞	∞	∞	∞	∞	-4
∞	∞	∞	-2	∞	∞	∞	-3	-4	3
-1	∞	∞	∞	∞	∞	-3	∞	∞	∞
1	∞	2	∞	1	∞	-4	∞	∞	3
∞	-4	∞	3	∞	-4	3	∞	3	∞

∞	3	∞	-2	7	2	∞	9	∞	∞
3	∞	-2	∞	∞	3	8	5	2	∞
∞	-2	∞	∞	∞	4	∞	-2	1	∞
-2	∞	∞	∞	9	1	2	∞	7	3
7	∞	∞	9	∞	∞	-2	∞	∞	-1
2	3	4	1	∞	∞	∞	6	∞	6
∞	8	∞	2	-2	∞	∞	∞	3	∞
9	5	-2	∞	∞	6	∞	∞	1	∞
∞	2	1	7	∞	∞	3	1	∞	9
∞	∞	∞	3	-1	6	∞	∞	9	∞

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	1	∞
-4	∞	0	∞	∞	∞	∞	∞	∞
∞	∞	3	0	∞	4	∞	12	∞
8	17	∞	10	0	∞	∞	∞	∞
∞	12	12	∞	∞	0	10	∞	∞
∞	∞	∞	∞	∞	∞	0	∞	∞
∞	∞	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	4	∞	∞	0

0	2	∞	∞	∞	12	∞	∞	∞
∞	0	1	∞	∞	∞	∞	∞	∞
∞	∞	0	∞	∞	∞	∞	∞	5
∞	∞	-3	0	∞	4	∞	2	∞
10	10	∞	10	0	∞	∞	∞	∞
∞	12	∞	∞	∞	0	10	∞	-5
∞	∞	∞	∞	∞	∞	0	∞	1
∞	1	∞	∞	∞	∞	7	0	∞
∞	∞	∞	∞	∞	∞	∞	-7	0

x	1	1	2	3	4	4	4	5	5	5	6	6	6	7	8	8	9
y	2	6	3	9	3	6	8	1	2	4	2	7	9	9	2	7	8
w	2	12	1	5	-3	4	2	10	10	10	12	10	-5	1	1	7	-7