Variational Wavefunction
Author
Vaibhav Sharma, Erich J Mueller
Title
Variational Wavefunction
Description
Supplemental notebook to "Rotating Bose gas dynamically enters the lowest Landau level"
Category
Academic Articles & Supplements
Keywords
rotating Bose gas, condensed Bose gas, Landau level, equations of motion, condensate, wavefunction, quantum Hall state
URL
http://www.notebookarchive.org/2022-01-ch0y8sw/
DOI
https://notebookarchive.org/2022-01-ch0y8sw
Date Added
2022-01-27
Date Last Modified
2022-01-27
File Size
1.49 megabytes
Supplements
Rights
Redistribution rights reserved

This file contains supplementary data for Vaibhav Sharma and Erich J Mueller “Rotating Bose gas dynamically enters the lowest Landau level,” https://arxiv.org/abs/2111.10415.
Variational Wavefunction
Variational Wavefunction
Vaibhav Sharma and Erich J Mueller
In[]:=
g=1000(*Interactionstrength*)
Out[]=
1000
In[]:=
r=0;(*Initialrotationrate*)
eps=0.125;(*Constantdeformation*)
(*Minimizingenergyininitialstatetofindinitialparametervalues*)
In[]:=
energy=1/(2lx[t]^2)+2phix[t]^2lx[t]^2+2phix[t]^2a[t]^2ly[t]^2+phixy[t]^2ly[t]^2/2+2phix[t]phixy[t]ly[t]^2a[t]+1/(2ly[t]^2)+a[t]^2/(2lx[t]^2)+2phiy[t]^2ly[t]^2+phixy[t]^2lx[t]^2/2+0.5a[t]^2phixy[t]^2ly[t]^2+2a[t]phiy[t]phixy[t]ly[t]^2+ra[t]phiy[t]ly[t]^2+0.5phixy[t]lx[t]^2r+0.5rphixy[t]a[t]^2ly[t]^2-ra[t]phix[t]ly[t]^2-0.5phixy[t]rly[t]^2-0.25a[t]epsly[t]^2+0.125lx[t]^2+0.125a[t]^2ly[t]^2+0.125ly[t]^2+g/(2Pilx[t]ly[t]);
In[]:=
en1=D[energy,lx[t]];
In[]:=
en2=D[energy,ly[t]];
In[]:=
en3=D[energy,a[t]];
In[]:=
en4=D[energy,phix[t]];
In[]:=
en5=D[energy,phiy[t]];
In[]:=
en6=D[energy,phixy[t]];
In[]:=
f=FindRoot[{en10,en20,en30,en40,en50,en60},{{lx[t],1},{ly[t],1},{phix[t],0},{phiy[t],0},{phixy[t],0},{a[t],0}}]
Out[]=
{lx[t]5.02136,ly[t]5.06056,phix[t]0.,phiy[t]0.,phixy[t]0.,a[t]0.12423}
(*Rotationbeingrampedupandconstantepsilondeformation*)
In[]:=
timerot=64;
In[]:=
r=Sin[Pi/(2timerot)t]HeavisideTheta[timerot-t]+HeavisideTheta[t-timerot];
In[]:=
energy=1/(2lx[t]^2)+2phix[t]^2lx[t]^2+2phix[t]^2a[t]^2ly[t]^2+phixy[t]^2ly[t]^2/2+2phix[t]phixy[t]ly[t]^2a[t]+1/(2ly[t]^2)+a[t]^2/(2lx[t]^2)+2phiy[t]^2ly[t]^2+phixy[t]^2lx[t]^2/2+0.5a[t]^2phixy[t]^2ly[t]^2+2a[t]phiy[t]phixy[t]ly[t]^2+ra[t]phiy[t]ly[t]^2+0.5phixy[t]lx[t]^2r+0.5rphixy[t]a[t]^2ly[t]^2-ra[t]phix[t]ly[t]^2-0.5phixy[t]rly[t]^2-0.25a[t]epsly[t]^2+0.125lx[t]^2+0.125a[t]^2ly[t]^2+0.125ly[t]^2+g/(2Pilx[t]ly[t]);
In[]:=
T=-phix'[t]lx[t]^2/2-phix'[t]a[t]^2ly[t]^2/2-phiy'[t]ly[t]^2/2-phixy'[t]a[t]ly[t]^2/2;
In[]:=
S=T-energy;(*Action*)
In[]:=
EulerLagrange1=-D[D[S,lx'[t]],t]+D[S,lx[t]]
Out[]=
1
3
lx[t]
2
a[t]
3
lx[t]
500
πly[t]
2
lx[t]
2
phix[t]
2
phixy[t]
πt
128
′
phix
In[]:=
EulerLagrange2=-D[D[S,ly'[t]],t]+D[S,ly[t]]
Out[]=
1
3
ly[t]
500
πlx[t]
2
ly[t]
2
a[t]
2
a[t]
2
phix[t]
2
phixy[t]
2
a[t]
2
phixy[t]
2
phiy[t]
πt
128
πt
128
2
a[t]
πt
128
πt
128
2
a[t]
′
phix
′
phixy
′
phiy
In[]:=
EulerLagrange3=-D[D[S,a'[t]],t]+D[S,a[t]]
Out[]=
-+0.03125-0.25a[t]-4a[t]-2phix[t]phixy[t]-1.a[t]-2phixy[t]phiy[t]+phix[t]HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin-1.a[t]phixy[t]HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin-phiy[t]HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin-a[t][t]-[t]
a[t]
2
lx[t]
2
ly[t]
2
ly[t]
2
ly[t]
2
phix[t]
2
ly[t]
2
ly[t]
2
phixy[t]
2
ly[t]
2
ly[t]
πt
128
2
ly[t]
πt
128
2
ly[t]
πt
128
2
ly[t]
′
phix
1
2
2
ly[t]
′
phixy
In[]:=
EulerLagrange4=-D[D[S,phix'[t]],t]+D[S,phix[t]]
Out[]=
-4phix[t]-4phix[t]-2a[t]phixy[t]+a[t]HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin+a[t][t]+lx[t][t]+ly[t][t]
2
lx[t]
2
a[t]
2
ly[t]
2
ly[t]
2
ly[t]
πt
128
2
ly[t]
′
a
′
lx
2
a[t]
′
ly
In[]:=
EulerLagrange5=-D[D[S,phiy'[t]],t]+D[S,phiy[t]]
Out[]=
-2a[t]phixy[t]-4phiy[t]-a[t]HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin+ly[t][t]
2
ly[t]
2
ly[t]
2
ly[t]
πt
128
′
ly
In[]:=
EulerLagrange6=-D[D[S,phixy'[t]],t]+D[S,phixy[t]]
Out[]=
-2a[t]phix[t]-phixy[t]-phixy[t]-1.phixy[t]-2a[t]phiy[t]-0.5HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin+0.5HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin-0.5HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin+[t]+a[t]ly[t][t]
2
ly[t]
2
lx[t]
2
ly[t]
2
a[t]
2
ly[t]
2
ly[t]
2
lx[t]
πt
128
2
ly[t]
πt
128
2
a[t]
2
ly[t]
πt
128
1
2
2
ly[t]
′
a
′
ly
In[]:=
x=lx[t]/.f;
In[]:=
y=ly[t]/.f;
In[]:=
al=a[t]/.f;
In[]:=
s2=NDSolve[{EulerLagrange10,EulerLagrange20,EulerLagrange30,EulerLagrange40,EulerLagrange50,EulerLagrange60,lx[0]x,ly[0]y,phix[0]0.,phiy[0]0.,phixy[0]0.,a[0]al},{lx,ly,phix,phiy,phixy,a},{t,0,160},WorkingPrecision10]

1
3
lx[t]
2
a[t]
3
lx[t]
500
πly[t]
2
lx[t]
2
phix[t]
2
phixy[t]
′
phix
Out[]=
lxInterpolatingFunction
,lyInterpolatingFunction
,phixInterpolatingFunction
,phiyInterpolatingFunction
,phixyInterpolatingFunction
,aInterpolatingFunction
|
|
|
|
|
|
In[]:=
p11=Plot[Evaluate[lx[16t]/.s2],{t,0,10},PlotRangeAll,TicksStyleMedium,AxesOrigin{0,0}]
Out[]=

In[]:=
p12=Plot[Evaluate[Log[ly[16t]]/.s2],{t,0,10},PlotRangeAll,PlotStyle{Red,Dashed,Thick},TicksStyleMedium,PlotStyleRed,AxesOrigin{0,0}]
Out[]=

In[]:=
p13=Plot[Evaluate[phixy[16t]/.s2],{t,0,8},PlotRangeAll,TicksStyleMedium]
Out[]=

In[]:=
p14=Plot[Evaluate[a[16t]/.s2],{t,0,10},PlotStyle{Red,Dashed,Thick},TicksStyleMedium,PlotStyleRed]
Out[]=

In[]:=
n=a[160]/.s2
Out[]=
{0.01561299294}
In[]:=
p15=Plot[Evaluate[phiy[16t]/.s2],{t,0,10},PlotRangeAll,TicksStyleMedium]
Out[]=

In[]:=
n1=phiy[160]/.s2
Out[]=
{0.007808925227}
In[]:=
p16=Plot[Evaluate[phix[16t]/.s2],{t,0,10},PlotRangeAll,PlotStyle{Red,Dashed,Thick},TicksStyleMedium,PlotStyleRed]
Out[]=

In[]:=
n2=phix[160]/.s2
Out[]=
{0.007763874023}
(*Averagelandauleveloccupationthroughenergyinlandaulevels*)
In[]:=
energylandau=1/(2lx[t]^2)+2phix[t]^2lx[t]^2+2phix[t]^2a[t]^2ly[t]^2+phixy[t]^2ly[t]^2/2+2phix[t]phixy[t]ly[t]^2a[t]+1/(2ly[t]^2)+a[t]^2/(2lx[t]^2)+2phiy[t]^2ly[t]^2+phixy[t]^2lx[t]^2/2+0.5a[t]^2phixy[t]^2ly[t]^2+2a[t]phiy[t]phixy[t]ly[t]^2+a[t]phiy[t]ly[t]^2+0.5phixy[t]lx[t]^2+0.5phixy[t]a[t]^2ly[t]^2-a[t]phix[t]ly[t]^2-0.5phixy[t]ly[t]^2+0.125lx[t]^2+0.125a[t]^2ly[t]^2+0.125ly[t]^2;
In[]:=
p20=Plot[Evaluate[Log[energylandau]/.s2],{t,0,160},PlotRangeAll]
Out[]=
In[]:=
Plot[Evaluate[energy/.s2],{t,0,160},PlotRangeAll,AxesLabel{tω,totalenergy}]
Out[]=

(*Deformedlandaulevelaverageoccupationthroughenergyindeformedlevels*)
In[]:=
defenergylandau=(1/(2lx[t]^2)+2(phix[t]+2rn2)^2lx[t]^2+2(phix[t]+2rn2)^2a[t]^2ly[t]^2+phixy[t]^2ly[t]^2/2+2(phix[t]+2rn2)phixy[t]ly[t]^2a[t]+1/(2ly[t]^2)+a[t]^2/(2lx[t]^2)+2(phiy[t]-2rn1)^2ly[t]^2+phixy[t]^2lx[t]^2/2+0.5a[t]^2phixy[t]^2ly[t]^2+2a[t](phiy[t]-2rn1)phixy[t]ly[t]^2)/Sqrt[1+0.125^2/4]+a[t](phiy[t]-2rn1)ly[t]^2+0.5phixy[t]lx[t]^2+0.5phixy[t]a[t]^2ly[t]^2-a[t](phix[t]+2rn2)ly[t]^2-0.5phixy[t]ly[t]^2+(0.125lx[t]^2+0.125a[t]^2ly[t]^2+0.125ly[t]^2)Sqrt[1+0.125^2/4];
In[]:=
Plot[Evaluate[Log[defenergylandau/.s2]],{t,0,160},PlotRangeAll,AxesLabel{tω,totalenergy}]
Out[]=

(*Whendeformationepsilonisgraduallyswitchedoff*)
In[]:=
timeeps=64;(*Switchofftimeforepsilon*)
In[]:=
eps=0.125HeavisideTheta[timerot-t]+0.125HeavisideTheta[t-timerot](timerot+timeeps-t)/timeeps;
In[]:=
energy=1/(2lx[t]^2)+2phix[t]^2lx[t]^2+2phix[t]^2a[t]^2ly[t]^2+phixy[t]^2ly[t]^2/2+2phix[t]phixy[t]ly[t]^2a[t]+1/(2ly[t]^2)+a[t]^2/(2lx[t]^2)+2phiy[t]^2ly[t]^2+phixy[t]^2lx[t]^2/2+0.5a[t]^2phixy[t]^2ly[t]^2+2a[t]phiy[t]phixy[t]ly[t]^2+ra[t]phiy[t]ly[t]^2+0.5phixy[t]lx[t]^2r+0.5rphixy[t]a[t]^2ly[t]^2-ra[t]phix[t]ly[t]^2-0.5phixy[t]rly[t]^2-0.25a[t]epsly[t]^2+0.125lx[t]^2+0.125a[t]^2ly[t]^2+0.125ly[t]^2+g/(2Pilx[t]ly[t]);
In[]:=
S=T-energy;(*Action*)
In[]:=
EulerLagrange1=-D[D[S,lx'[t]],t]+D[S,lx[t]]
Out[]=
1
3
lx[t]
2
a[t]
3
lx[t]
500
πly[t]
2
lx[t]
2
phix[t]
2
phixy[t]
πt
128
′
phix
In[]:=
EulerLagrange2=-D[D[S,ly'[t]],t]+D[S,ly[t]]
Out[]=
1
3
ly[t]
500
πlx[t]
2
ly[t]
2
a[t]
2
a[t]
2
phix[t]
2
phixy[t]
2
a[t]
2
phixy[t]
2
phiy[t]
πt
128
πt
128
2
a[t]
πt
128
πt
128
2
a[t]
′
phix
′
phixy
′
phiy
In[]:=
EulerLagrange3=-D[D[S,a'[t]],t]+D[S,a[t]]
Out[]=
--0.25a[t]+0.25(0.125HeavisideTheta[64-t]+0.00195313(128-t)HeavisideTheta[-64+t])-4a[t]-2phix[t]phixy[t]-1.a[t]-2phixy[t]phiy[t]+phix[t]HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin-1.a[t]phixy[t]HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin-phiy[t]HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin-a[t][t]-[t]
a[t]
2
lx[t]
2
ly[t]
2
ly[t]
2
ly[t]
2
phix[t]
2
ly[t]
2
ly[t]
2
phixy[t]
2
ly[t]
2
ly[t]
πt
128
2
ly[t]
πt
128
2
ly[t]
πt
128
2
ly[t]
′
phix
1
2
2
ly[t]
′
phixy
In[]:=
EulerLagrange4=-D[D[S,phix'[t]],t]+D[S,phix[t]]
Out[]=
-4phix[t]-4phix[t]-2a[t]phixy[t]+a[t]HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin+a[t][t]+lx[t][t]+ly[t][t]
2
lx[t]
2
a[t]
2
ly[t]
2
ly[t]
2
ly[t]
πt
128
2
ly[t]
′
a
′
lx
2
a[t]
′
ly
In[]:=
EulerLagrange5=-D[D[S,phiy'[t]],t]+D[S,phiy[t]]
Out[]=
-2a[t]phixy[t]-4phiy[t]-a[t]HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin+ly[t][t]
2
ly[t]
2
ly[t]
2
ly[t]
πt
128
′
ly
In[]:=
EulerLagrange6=-D[D[S,phixy'[t]],t]+D[S,phixy[t]]
Out[]=
-2a[t]phix[t]-phixy[t]-phixy[t]-1.phixy[t]-2a[t]phiy[t]-0.5HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin+0.5HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin-0.5HeavisideTheta[-64+t]+HeavisideTheta[64-t]Sin+[t]+a[t]ly[t][t]
2
ly[t]
2
lx[t]
2
ly[t]
2
a[t]
2
ly[t]
2
ly[t]
2
lx[t]
πt
128
2
ly[t]
πt
128
2
a[t]
2
ly[t]
πt
128
1
2
2
ly[t]
′
a
′
ly
In[]:=
s2=NDSolve[{EulerLagrange10,EulerLagrange20,EulerLagrange30,EulerLagrange40,EulerLagrange50,EulerLagrange60,lx[0]x,ly[0]y,phix[0]0.,phiy[0]0.,phixy[0]0.,a[0]al},{lx,ly,phix,phiy,phixy,a},{t,0,timerot+timeeps},WorkingPrecision10]

1
3
lx[t]
2
a[t]
3
lx[t]
500
πly[t]
2
lx[t]
2
phix[t]
2
phixy[t]
′
phix
Out[]=
lxInterpolatingFunction
,lyInterpolatingFunction
,phixInterpolatingFunction
,phiyInterpolatingFunction
,phixyInterpolatingFunction
,aInterpolatingFunction
|
|
|
|
|
|
In[]:=
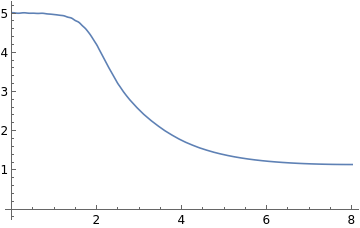
p11=Plot[Evaluate[lx[16t]/.s2],{t,0,(timerot+timeeps)/16},PlotRangeAll,TicksStyleMedium,AxesOrigin{0,0}]
Out[]=
In[]:=
p12=Plot[Evaluate[Log[ly[16t]]/.s2],{t,0,(timerot+timeeps)/16},PlotRangeAll,PlotStyle{Red,Dashed,Thick},TicksStyleMedium,PlotStyleRed,AxesOrigin{0,0}]
Out[]=

In[]:=
p13=Plot[Evaluate[phixy[16t]/.s2],{t,0,(timerot+timeeps)/16},PlotRangeAll,TicksStyleMedium]
Out[]=

In[]:=
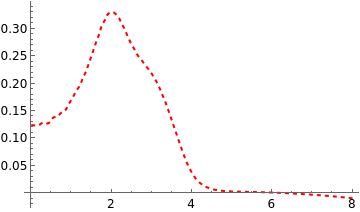
p14=Plot[Evaluate[a[16t]/.s2],{t,0,(timerot+timeeps)/16},PlotStyle{Red,Dashed,Thick},TicksStyleMedium,PlotStyleRed]
Out[]=
In[]:=
n=a[160]/.s2
Out[]=
{0.01561299294}
In[]:=
p15=Plot[Evaluate[phiy[16t]/.s2],{t,0,(timerot+timeeps)/16},PlotRangeAll,TicksStyleMedium]
Out[]=

In[]:=
p16=Plot[Evaluate[phix[16t]/.s2],{t,0,(timerot+timeeps)/16},PlotRangeAll,PlotStyle{Red,Dashed,Thick},TicksStyleMedium,PlotStyleRed]
Out[]=

(*Averagelandauleveloccupationthroughenergyinlandaulevels*)
In[]:=
energylandau=1/(2lx[t]^2)+2phix[t]^2lx[t]^2+2phix[t]^2a[t]^2ly[t]^2+phixy[t]^2ly[t]^2/2+2phix[t]phixy[t]ly[t]^2a[t]+1/(2ly[t]^2)+a[t]^2/(2lx[t]^2)+2phiy[t]^2ly[t]^2+phixy[t]^2lx[t]^2/2+0.5a[t]^2phixy[t]^2ly[t]^2+2a[t]phiy[t]phixy[t]ly[t]^2+a[t]phiy[t]ly[t]^2+0.5phixy[t]lx[t]^2+0.5phixy[t]a[t]^2ly[t]^2-a[t]phix[t]ly[t]^2-0.5phixy[t]ly[t]^2+0.125lx[t]^2+0.125a[t]^2ly[t]^2+0.125ly[t]^2;
In[]:=
p20=Plot[Evaluate[energylandau/.s2],{t,0,(timerot+timeeps)},PlotRangeAll]
Out[]=
In[]:=
Plot[Evaluate[energy/.s2],{t,0,(timerot+timeeps)},PlotRangeAll,AxesLabel{tω,totalenergy}]
Out[]=

Cite this as: Vaibhav Sharma, Erich J Mueller, "Variational Wavefunction" from the Notebook Archive (2022), https://notebookarchive.org/2022-01-ch0y8sw
Download
