NIL: Learning Nonlinear Interpolants
Author
Mingshuai Chen
Title
NIL: Learning Nonlinear Interpolants
Description
A learning-based tool in Mathematica that is dedicated to synthesizing nontrivial (reverse) Craig interpolants for the quantifier-free theory of nonlinear arithmetic.
Category
Academic Articles & Supplements
Keywords
Nonlinear Craig interpolant, counterexample-guided learning, program verification, support vector machines (SVMs)
URL
http://www.notebookarchive.org/2021-08-5lcsyb7/
DOI
https://notebookarchive.org/2021-08-5lcsyb7
Date Added
2021-08-12
Date Last Modified
2021-08-12
File Size
3.52 megabytes
Supplements
Rights
CC BY-NC-SA 4.0

NIL: learning nonlinear interpolant
NIL: learning nonlinear interpolant
The tool NIL is dedicated to synthesizing nontrivial (reverse) Craig interpolants for the quantifier-free theory of nonlinear arithmetic. It takes as input a pair (φ, ψ) of mutually contradictory formulas over the reals, and generates an interpolant I for (φ, ψ) s.t. φ ⊨ I and I ∧ ψ ⊨ False. NIL views interpolants as classifiers and adopts the sampling-guessing-refining philosophy, namely in each iteration it is fed with a classifier over a finite set of sample points from φ and ψ, and generates a bunch of counter-examples as new sample points to refine further classifiers, until a candidate classifier can be verified to be a real interpolant. LIBSVM is integrated as an engine to perform the classifications.
Current version: v1.1
Validated on platform: Mathematica 10, 64bit-Ubuntu-Desktop-16.04/Windows-10
Latest modification: on Aug. 31, 2021, by Mingshuai Chen, RWTH Aachen
Corresponding e-mail: chenms@cs.rwth-aachen.de
List of contributors: Mingshuai Chen, Jian Wang, Jie An, Bohua Zhan, Deepak Kapur, and Naijun Zhan
Comments and bug-reports are highly appreciated.
© 2021 NIL, Lehrstuhl für Informatik 2, RWTH Aachen University. All rights reserved.
Current version: v1.1
Validated on platform: Mathematica 10, 64bit-Ubuntu-Desktop-16.04/Windows-10
Latest modification: on Aug. 31, 2021, by Mingshuai Chen, RWTH Aachen
Corresponding e-mail: chenms@cs.rwth-aachen.de
List of contributors: Mingshuai Chen, Jian Wang, Jie An, Bohua Zhan, Deepak Kapur, and Naijun Zhan
Comments and bug-reports are highly appreciated.
© 2021 NIL, Lehrstuhl für Informatik 2, RWTH Aachen University. All rights reserved.
Source code
Source code
In[]:=
Benchmark A: working perfectly even w/o rounding.
Benchmark A: working perfectly even w/o rounding.
Dummy
Dummy
consPhi0=x<-1;consPsi0=x≥1;degree0=1;initialRange0={-3,3};
main[consPhi0,consPsi0,degree0,initialRange0]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 0.00127295-0.497151(1-1.00414x)+0.497151(1+1.00158x)<0
Verifying the candidate ...
Valid interpolant (simplified): 0.00127659+1.x<0
Improved valid interpolant (rounded under precision 1.): x<0
Elapsed time: 0.108178
Done.
Necklace
Necklace
consPhi1=y-x^2-10;consPsi1=y+x^2+10;degree1=1;initialRange1={-3,3};
main[consPhi1,consPsi1,degree1,initialRange1]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 6.93889×+0.499968(1+0.00565291x-1.00003y)-0.499968(1+0.00565291x+1.00003y)<0
-18
10
Verifying the candidate ...
Valid interpolant (simplified): y>0
Improved valid interpolant (rounded under precision 1.): -y<0
Elapsed time: 0.212085
Rendering graphics ...
 |
|
Done.
Face
Face
consPhi2=(x+4)^2+y^2-1≤0||(x-4)^2+y^2-1≤0;consPsi2=x^2+y^2-64≤0&&(x+4)^2+y^2-9≥0&&(x-4)^2+y^2-9≥0;degree2=4;initialRange2={-8,8};
main[consPhi2,consPsi2,degree2,initialRange2]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 1.25304+0.000205205+0.0000465005-0.000144477+0.0028645-0.00218592-0.0044507+0.00024569+0.00303519+0.000384008<0
4
(1+1.45875x-1.73077y)
4
(1-6.7585x-1.24955y)
4
(1+3.94449x-0.888344y)
4
(1-1.02474x-0.672376y)
4
(1-3.22834x-0.352833y)
4
(1+3.1343x+0.405752y)
4
(1+7.02933x+0.578535y)
4
(1+1.16898x+1.13553y)
4
(1-1.24395x+1.33052y)
Verifying the candidate ...
Valid interpolant (simplified): 223.586+1.+(0.203313-0.627199y)+0.609577y+5.93026+2.33448+1.52974+(-49.5719-1.31492y+4.96677)+x(-4.00815-3.00414y+3.25148+2.50913)<0
4
x
3
x
2
y
3
y
4
y
2
x
2
y
2
y
3
y
Improved valid interpolant (rounded under precision 0.001): 1++-y++++--++x--++<0
4
x
223
y
366
3
x
356
2
y
37
3
y
95
4
y
146
2
x
2
9
y
170
2
y
45
1
55
y
74
2
y
68
3
y
89
Elapsed time: 0.329295
Rendering graphics ...
 |
|
Done.
Twisted
Twisted
consPhi3=-2*x*y^2+x^2+3*x*z-y^2-y*z+z^2-1≥0&&x^2*z^2+y^2*z^2-x^2-y^2+1/6*(x^4+2*x^2*y^2+y^4)-1/120*(x^6+y^6)-4≤0;consPsi3=4*(x-y)^4+(x+y)^2+w^2-80≤0&&100*(x+y)^2-w^2*(x-y)^4-3000≥0;degree3=4;initialRange3={-10,10};
main[consPhi3,consPsi3,degree3,initialRange3]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: -1.1155-0.000121252-0.000298621+0.0017033+0.00113251-0.0000340746-0.00196064-0.00122533+0.000639618+0.000164498<0
4
(1-6.68365x-5.84104y)
4
(1-2.3186x-4.83191y)
4
(1-2.27591x-3.31191y)
4
(1-3.27206x-2.31721y)
4
(1-4.5224x-1.94946y)
4
(1-0.956471x-0.15072y)
4
(1+2.96612x+0.822385y)
4
(1+4.01709x+2.40146y)
4
(1+2.24566x+3.80465y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-6.29179,y-5.02263,z-0.547621,w4.1},{x-6.18707,y-4.77132,z-0.399048,w0.2},{x-6.40467,y-5.70101,z-0.535211,w0.1},{x-1.30665,y-3.29288,z-0.277076,w-2.1},{x-6.19437,y-6.0291,z-0.507104,w0.6},{x-6.3101,y-5.66667,z-0.0366972,w-4.7},{x-1.9875,y-1.57211,z0.807579,w-2.7},{x-6.09789,y-6.11802,z0.192661,w-3.9},{x-5.92312,y-6.15712,z0.0588235,w0.7},{x-6.18215,y-4.86575,z0.227883,w-0.3},{x-5.88788,y-6.16028,z0.0730744,w-1.2},{x-1.84464,y-2.14414,z-0.010989,w-3.5},{x-5.94343,y-6.1547,z-0.243159,w2.2},{x-2.63095,y-1.3664,z-0.557599,w3.1},{x-1.22434,y-3.0625,z0.333333,w0},{x-1.71488,y-2.70476,z0.0384615,w4.1},{x-3.14345,y-1.46486,z0.0583327,w3.4},{x-1.33693,y-3.35373,z0.0689655,w1.7},{x-1.21936,y-2.51626,z-0.694687,w3.9},{x-6.12344,y-4.70148,z0.122442,w2.6},{x-6.15689,y-5.89579,z0.0830645,w-3.3},{x-6.14304,y-6.09919,z-0.514546,w1.6},{x-5.94469,y-6.15454,z0.245695,w-0.8},{x-6.21344,y-4.92927,z-0.320788,w1.3},{x-6.00267,y-6.14481,z-0.343912,w4.8},{x-5.95036,y-6.13509,z-0.166367,w1.1},{x-6.3101,y-5.07522,z0.11236,w2.8},{x-5.95143,y-6.13776,z0.185664,w-4.4},{x-6.12814,y-6.03947,z0.148148,w4.2}}
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: -5.13781-0.000656208-0.000149865-0.000160716-0.000233023+0.0190264-0.0213158+0.00179226-0.0000933163+0.000850859+0.000939383<0
4
(1-4.21549x-6.28511y)
4
(1-5.88788x-6.16028y)
4
(1-2.3186x-4.83191y)
4
(1-6.12344x-4.70148y)
4
(1-2.27591x-3.31191y)
4
(1-1.71488x-2.70476y)
4
(1-3.27206x-2.31721y)
4
(1+5.2139x+1.02834y)
4
(1+4.01709x+2.40146y)
4
(1+2.24566x+3.80465y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-3.26819,y-5.46494,z-0.203046,w0.1},{x-3.56955,y-1.92124,z-2.4,w-1.41968},{x-3.71759,y-5.78344,z0.0306122,w-3.7},{x-3.74008,y-5.89936,z-0.169231,w2.6},{x-3.70002,y-1.90667,z-4.4,w2.68175},{x-3.65077,y-5.85155,z-0.776803,w4.3},{x-3.64902,y-1.83427,z-3.3,w-0.323077},{x-3.31944,y-5.63383,z0.677997,w0.5},{x-3.39405,y-5.69055,z0.71403,w3.7},{x-1.95303,y-3.74444,z4.8,w2.5187},{x-3.64074,y-1.87559,z-4.,w-0.625},{x-3.73359,y-1.93651,z3.1,w-2.47611},{x-1.91806,y-3.74171,z-0.6,w1.9302},{x-1.79862,y-3.67877,z1.4,w-0.0359712},{x-3.60806,y-5.73737,z-0.549593,w1.9},{x-3.65579,y-5.87104,z-0.412698,w-3.2},{x-1.91806,y-3.74171,z-0.7,w-1.9302},{x-3.67887,y-1.90337,z1.4,w-3.01464},{x-3.67506,y-5.88323,z-0.209677,w3.1},{x-3.82984,y-1.9869,z-2.5,w0.151181},{x-3.73868,y-5.70621,z0.,w1.3},{x-3.53803,y-5.7933,z0.773608,w-0.1},{x-1.95774,y-3.6146,z-2.9,w-0.357143},{x-3.65833,y-5.80745,z0.328947,w-4.9},{x-3.69554,y-5.88842,z0.809066,w-1.9},{x-3.67882,y-1.80007,z4.2,w-0.383253},{x-3.67901,y-5.88571,z-0.820527,w-3.8},{x-3.59342,y-1.92541,z4.8,w2.43096},{x-3.65104,y-1.95011,z5.,w-3.89175}}
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant: -10.6484-0.0228038-0.000343804+0.108022-0.0330395-0.0705039-0.0103795+0.025389+0.00104046+0.00261877<0
4
(1-2.3186x-4.83191y)
4
(1-6.12344x-4.70148y)
4
(1-1.79862x-3.67877y)
4
(1-1.33693x-3.35373y)
4
(1-1.71488x-2.70476y)
4
(1-4.5224x-1.94946y)
4
(1-3.67882x-1.80007y)
4
(1+4.01709x+2.40146y)
4
(1+2.24566x+3.80465y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x3.45937,y2.03982,z0,w2.43663},{x1.9493,y3.77231,z3.8,w-1.7562},{x3.66563,y1.82248,z5.,w1.01684},{x3.67899,y1.81433,z1.9,w-1.20852},{x2.03011,y3.80282,z-0.4,w2.54476},{x3.67899,y1.80995,z2.9,w0.2},{x2.0316,y3.73011,z4.8,w3.67569},{x-5.60661,y-3.55198,z-0.0122783,w2.5},{x3.5482,y2.05746,z2.6,w5.36859},{x3.67891,y1.80008,z-3.3,w0.255474},{x3.66672,y1.89828,z-3.8,w-0.470588},{x2.0316,y3.57797,z-4.2,w-2.6},{x1.91745,y3.77476,z-1.1,w0},{x3.67897,y1.80985,z-3.2,w1.0207},{x1.93651,y3.6515,z1.8,w-0.857143},{x3.67889,y1.81622,z3.8,w1.27687},{x3.5134,y2.03896,z-2.5,w4.18755},{x1.87645,y3.60077,z-4.8,w0},{x3.67901,y1.81388,z0.7,w-1.19178},{x1.98826,y3.60819,z1.,w4.37862},{x1.96646,y3.61491,z2.6,w3.76923},{x3.67885,y1.81306,z1.9,w1.15259},{x3.6788,y1.82453,z2.7,w-1.55719},{x3.54232,y2.06519,z3.,w-5.43261},{x3.46666,y2.04363,z1.1,w-0.588235},{x3.60588,y1.87135,z-0.9,w0},{x1.90319,y3.62849,z1.3,w1.95},{x2.23692,y3.99744,z-4.2,w-0.645161},{x2.04347,y3.87465,z4.6,w0},{x1.86774,y3.67417,z-0.9,w-0.75}}
Learning a candidate interpolant at step 4 ...
Synthesized candidate interpolant: -11.0062-0.0257613+0.12249-0.000631156-0.0379806-0.0810112-0.011738+0.0290792+0.00204697+0.00350605<0
4
(1-2.3186x-4.83191y)
4
(1-1.79862x-3.67877y)
4
(1-5.60661x-3.55198y)
4
(1-1.33693x-3.35373y)
4
(1-1.71488x-2.70476y)
4
(1-4.5224x-1.94946y)
4
(1-3.67882x-1.80007y)
4
(1+3.67891x+1.80008y)
4
(1+1.86774x+3.67417y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-4.84696,y-2.40422,z-0.0123609,w-2.6},{x-5.05976,y-2.67867,z-0.139188,w0.3},{x-5.08538,y-2.7272,z0.0363036,w0.2},{x-4.86482,y-2.42774,z-0.0564346,w-1.1},{x-4.86482,y-2.42498,z-0.0825431,w-0.8},{x-4.84079,y-2.39713,z0.0535539,w-3.},{x-5.02245,y-2.62629,z-0.140908,w-3.2},{x-5.02957,y-2.63174,z0.161366,w2.4},{x-4.86087,y-2.42036,z0,w2.5},{x-4.85328,y-2.41217,z0.0641032,w-1.5},{x-4.84696,y-2.40702,z0.00564617,w4.4},{x-4.85328,y-2.41217,z0,w-4.4},{x-5.08538,y-2.70869,z0.167821,w-3.5},{x-5.23099,y-2.92943,z0.129998,w4.2},{x-5.23099,y-2.93172,z0.116139,w0.3},{x-5.08822,y-2.71412,z-0.161861,w-1.5},{x-5.20664,y-2.90011,z-0.0486656,w0.2},{x-5.23099,y-2.92943,z-0.0179949,w1.9},{x-5.1551,y-2.82775,z-0.00595238,w2.5},{x-5.03573,y-2.64005,z0.162507,w-3.},{x-5.08822,y-2.71272,z-0.167909,w-0.9},{x-5.23858,y-2.95183,z0.00318037,w1.1},{x-5.02245,y-2.6222,z-0.00949367,w-0.3},{x-5.29344,y-3.03582,z-1.89814×,w3.8},{x-4.95652,y-2.53998,z0.121548,w-1.9},{x-5.04585,y-2.66831,z0.0239617,w1.4},{x-5.1551,y-2.8105,z0.162183,w2.8},{x-4.85328,y-2.41153,z-0.0361613,w1.}}
-8
10
Learning a candidate interpolant at step 5 ...
Synthesized candidate interpolant: -10.8833-0.0260766+0.124504-0.0387075-0.0831946-0.00406131-0.00854882+0.0305137+0.00219452+0.00337696<0
4
(1-2.3186x-4.83191y)
4
(1-1.79862x-3.67877y)
4
(1-1.33693x-3.35373y)
4
(1-1.71488x-2.70476y)
4
(1-4.84079x-2.39713y)
4
(1-4.5224x-1.94946y)
4
(1-3.67882x-1.80007y)
4
(1+3.67891x+1.80008y)
4
(1+1.86774x+3.67417y)
Verifying the candidate ...
Valid interpolant (simplified): (-1.41063+0.9416y)+0.628457y+11.3225+(11.7913+2.08635y-0.710897)+x(-0.508114+15.8485y+2.52512+0.618257)<160.596+1.+1.70646+0.87528
3
x
2
y
2
x
2
y
2
y
3
y
4
x
3
y
4
y
Improved valid interpolant (rounded under precision 0.001): -1-+-+++--++-+x-+++<0
4
x
160
3
x
1
113
y
170
y
255
2
y
14
3
y
94
4
y
183
2
x
2
27
y
76
2
y
225
1
316
5y
51
2
y
63
3
y
259
Elapsed time: 140.624
Rendering graphics ...
 |
|
Done.
Ultimate
Ultimate
consPhi4=(x^2+y^2-3.8025≤0&&y≥0||(x-1)^2+y^2-0.9025≤0)&&(x-1)^2+y^2-0.09>0&&(x+1)^2+y^2-1.1025≥0||(x+1)^2+y^2-1/25≤0;consPsi4=(-3.8025++≤0&&-y≥0||-0.9025++≤0)&&-0.09++>0&&-1.1025++≥0||-1/25++≤0;degree4=7;initialRange4={-3,3};
2
x
2
y
2
(-1-x)
2
y
2
(-1-x)
2
y
2
(1-x)
2
y
2
(1-x)
2
y
main[consPhi4,consPsi4,degree4,initialRange4]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 0.316745+0.199307-0.131172+0.0722783+9.29644+0.111143+0.0808693-10.4795-1.26547+2.87447-4.53059-2.59893+18.543-12.5259-0.122714+0.60758-0.237833+0.143773-0.0368275<0
7
(1+0.604563x-0.986663y)
7
(1+1.31867x-0.858457y)
7
(1+1.75008x-0.770764y)
7
(1-0.0162503x-0.344779y)
7
(1-0.857655x-0.340969y)
7
(1-1.1633x-0.337402y)
7
(1+0.111031x-0.332308y)
7
(1+1.23426x-0.238492y)
7
(1+1.00569x-0.137088y)
7
(1+0.109347x+0.0644046y)
7
(1-0.815682x+0.0646479y)
7
(1-0.0587404x+0.0998781y)
7
(1+0.108693x+0.110587y)
7
(1+1.18867x+0.239869y)
7
(1-1.14429x+0.264585y)
7
(1-0.498312x+0.934735y)
7
(1-0.984483x+0.94402y)
7
(1-1.5666x+0.980881y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x0.832196,y0.10882},{x-0.136048,y0.651202},{x1.73512,y-0.749737},{x-1.60156,y0.952055},{x1.4974,y-0.809377},{x-1.54738,y0.969315},{x-0.264314,y0.773153},{x0.843233,y-0.124194},{x0.832339,y0.105251},{x0.816163,y0.0787643},{x1.77721,y-0.72426},{x1.10963,y0.279999},{x1.73323,y-0.751578},{x0.946194,y0.29808},{x-1.74352,y0.873285},{x1.84355,y-0.633121},{x-1.77661,y0.803842},{x-1.69808,y0.832759},{x0.366646,y-0.847045},{x0.832291,y0.10271},{x0.832471,y-0.109243},{x1.50882,y-0.791356},{x1.29798,y-0.89482},{x0.843995,y-0.0183903},{x0.965356,y0.306394},{x0.843995,y-0.0305254},{x1.51012,y-0.795956},{x0.195182,y-0.683573},{x1.28489,y-0.902548},{x-1.5396,y0.975495}}
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: 0.249625+0.0282828-0.0311583+0.700818+0.066274+10.6493+0.26461+0.0585193-12.7138-1.09456-0.307608+5.12547-0.227904-24.1224-3.60694+25.5571+0.959201-0.407203-0.902266-0.0302372+0.000392207+0.034095<0
7
(1+0.947723x-1.0537y)
7
(1+1.4974x-0.809377y)
7
(1+0.195182x-0.683573y)
7
(1+1.84355x-0.633121y)
7
(1-0.0162503x-0.344779y)
7
(1-0.857655x-0.340969y)
7
(1-1.1633x-0.337402y)
7
(1+0.111031x-0.332308y)
7
(1+1.17501x-0.29934y)
7
(1+1.23426x-0.238492y)
7
(1+0.832471x-0.109243y)
7
(1+0.649x+0.0207495y)
7
(1+0.109347x+0.0644046y)
7
(1-0.815682x+0.0646479y)
7
(1-0.0587404x+0.0998781y)
7
(1-1.14429x+0.264585y)
7
(1+0.946194x+0.29808y)
7
(1-0.136048x+0.651202y)
7
(1-1.77661x+0.803842y)
7
(1-1.34151x+0.878829y)
7
(1-0.984483x+0.94402y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-1.23862,y0.918155},{x-1.25861,y0.912812},{x1.08161,y-0.289282},{x-1.21774,y0.924711},{x-1.65977,y0.822061},{x-1.82204,y0.653267},{x1.09728,y-0.285084},{x-1.22142,y0.923836},{x-1.26202,y0.912441},{x-1.83665,y0.655146},{x-1.24249,y0.918531},{x-1.69621,y0.79531},{x-1.2386,y0.919548},{x1.84645,y-0.624009},{x-1.18082,y0.932633},{x-1.84612,y0.622105},{x1.84943,y-0.617226},{x1.84692,y-0.620666},{x-1.21801,y-0.210402},{x-1.73105,y0.808832},{x-1.23257,y-0.190642},{x1.11484,y-0.281721},{x-0.814891,y-0.257182},{x1.84289,y-0.626134},{x1.09622,y-0.284849},{x-1.81749,y0.658946},{x-1.24427,y0.917354},{x-1.2016,y0.927992},{x1.07866,y-0.289678},{x1.8491,y-0.617675}}
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant: 0.251275+0.0315703+0.667552+0.0500918+8.24849-10.1086-1.63337-0.556775+1.06674+0.00886743+6.27748-29.0549-5.31727+30.3661-0.0289902+1.46449-0.535029-0.0462341-0.900238<0
7
(1+0.947723x-1.0537y)
7
(1+0.195182x-0.683573y)
7
(1+1.84943x-0.617226y)
7
(1-0.0162503x-0.344779y)
7
(1+0.111031x-0.332308y)
7
(1+1.09622x-0.284849y)
7
(1+1.11484x-0.281721y)
7
(1-0.814891x-0.257182y)
7
(1-1.23257x-0.190642y)
7
(1+0.832471x-0.109243y)
7
(1+0.109347x+0.0644046y)
7
(1-0.815682x+0.0646479y)
7
(1-0.0587404x+0.0998781y)
7
(1+1.18867x+0.239869y)
7
(1-1.14429x+0.264585y)
7
(1+0.946194x+0.29808y)
7
(1-1.84612x+0.622105y)
7
(1-0.136048x+0.651202y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-1.19746,y1.04116},{x1.3004,y-0.0752688},{x1.31365,y-1.01663},{x1.32145,y-0.999585},{x1.41775,y-0.963319},{x1.31477,y-0.0234261},{x1.21073,y-0.21804},{x1.2394,y-1.02234},{x1.28717,y0.0943035},{x1.25435,y-1.02897},{x1.50526,y-0.920441},{x1.0967,y-1.04785},{x1.23907,y-0.198025},{x1.26375,y-0.16906},{x1.15721,y-1.04714},{x1.3114,y-1.00276},{x1.30087,y-0.130809},{x1.08808,y-1.0463},{x1.45391,y-0.94682},{x1.26482,y0.144365},{x1.16762,y-1.04163},{x1.31778,y-1.00076},{x-1.28275,y1.05174},{x1.21813,y-1.03445},{x1.26998,y-1.0147},{x-0.873239,y1.04232},{x1.28337,y-0.110594},{x1.20842,y-1.02911},{x1.3114,y-1.02133},{x1.27683,y-1.01285}}
Learning a candidate interpolant at step 4 ...
Synthesized candidate interpolant: 0.243245+0.0158358+0.77764+0.0539098+8.68704-10.8998-1.98199+1.02742-0.286845+0.0106033+6.8356-0.787294-27.7741-5.21368+29.5327+1.43785-0.49588-0.0451168-0.892935-0.00103648<0
7
(1+1.08808x-1.0463y)
7
(1+0.195182x-0.683573y)
7
(1+1.84943x-0.617226y)
7
(1-0.0162503x-0.344779y)
7
(1+0.111031x-0.332308y)
7
(1+1.09622x-0.284849y)
7
(1-0.814891x-0.257182y)
7
(1+1.21073x-0.21804y)
7
(1-1.23257x-0.190642y)
7
(1+0.832471x-0.109243y)
7
(1+0.649x+0.0207495y)
7
(1+0.109347x+0.0644046y)
7
(1-0.815682x+0.0646479y)
7
(1-0.0587404x+0.0998781y)
7
(1-1.14429x+0.264585y)
7
(1+0.946194x+0.29808y)
7
(1-1.84612x+0.622105y)
7
(1-0.136048x+0.651202y)
7
(1-1.19746x+1.04116y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-0.0716748,y0.490624},{x-0.0374757,y0.422723},{x-0.0527184,y0.454681},{x-0.085,y0.515076},{x-0.056966,y0.461722},{x-0.0401699,y0.426946},{x-0.0305097,y0.406102},{x-0.0583252,y0.46532},{x-0.085,y0.515089},{x-0.0284951,y0.398938},{x-0.0420631,y0.42995},{x-0.0125114,y0.356884},{x-0.0527184,y0.455778},{x-0.0374757,y0.422574},{x-0.0367961,y0.418017},{x-0.056966,y0.464319},{x-0.0534466,y0.454463},{x-0.0170388,y0.369417},{x-0.0716748,y0.492054},{x-0.0534466,y0.457225},{x-0.0717961,y0.490854},{x-0.0527184,y0.452943},{x-0.0278641,y0.396802},{x-0.0576214,y0.464791},{x-0.033665,y0.411543},{x-0.0420631,y0.433108},{x-0.0716748,y0.490716},{x-0.0144903,y0.36267},{x-0.0420631,y0.433048},{x-0.0550728,y0.457835}}
Learning a candidate interpolant at step 5 ...
Synthesized candidate interpolant: 0.392557+1.34982+0.0515275+7.88808-12.9634-1.50618+1.18149-0.437811+5.75106-25.1144-5.6483+33.9908+1.54523-0.407134-5.88705-0.0472592+0.287378+0.00159908-0.0354633<0
7
(1+0.195182x-0.683573y)
7
(1+1.84943x-0.617226y)
7
(1-0.0162503x-0.344779y)
7
(1+0.111031x-0.332308y)
7
(1+1.09622x-0.284849y)
7
(1-0.814891x-0.257182y)
7
(1+1.21073x-0.21804y)
7
(1+0.832471x-0.109243y)
7
(1+0.109347x+0.0644046y)
7
(1-0.815682x+0.0646479y)
7
(1-0.0587404x+0.0998781y)
7
(1-1.14429x+0.264585y)
7
(1+0.946194x+0.29808y)
7
(1-0.0144903x+0.36267y)
7
(1-1.84612x+0.622105y)
7
(1-0.336689x+0.674633y)
7
(1-1.34151x+0.878829y)
7
(1-0.873239x+1.04232y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-1.84995,y0.616512},{x-1.84982,y0.616766},{x-1.84999,y0.616459},{x-1.84984,y0.616764},{x-1.43445,y0.840818},{x-1.84996,y0.616515},{x-1.84993,y0.616531},{x-1.84976,y0.616776},{x-1.84974,y0.61681},{x-1.84978,y0.616757},{x-1.84987,y0.616615},{x-1.84978,y0.616744},{x-1.84993,y0.616574},{x-1.44117,y0.84135},{x-1.41072,y0.856625},{x-1.84993,y0.616663},{x-1.84989,y0.616741},{x-1.84979,y0.61673},{x-1.51152,y0.796472},{x-1.84996,y0.616563},{x-1.8499,y0.616573},{x-1.47936,y0.820191},{x-1.56432,y0.764229},{x-1.84984,y0.616764},{x-1.84996,y0.616493},{x-1.84991,y0.616699},{x-1.84993,y0.616543},{x-1.85,y0.616442},{x-1.84973,y0.616812},{x-1.51063,y0.795187}}
Learning a candidate interpolant at step 6 ...
Synthesized candidate interpolant: 0.392666+1.35395+0.0514032+7.86972-12.9747-1.5015+1.19522-0.438209+5.73991-25.0503-5.67846+34.0147+1.55332-0.40545-5.96189-0.04789+0.317756+0.00311867-0.0407356<0
7
(1+0.195182x-0.683573y)
7
(1+1.84943x-0.617226y)
7
(1-0.0162503x-0.344779y)
7
(1+0.111031x-0.332308y)
7
(1+1.09622x-0.284849y)
7
(1-0.814891x-0.257182y)
7
(1+1.21073x-0.21804y)
7
(1+0.832471x-0.109243y)
7
(1+0.109347x+0.0644046y)
7
(1-0.815682x+0.0646479y)
7
(1-0.0587404x+0.0998781y)
7
(1-1.14429x+0.264585y)
7
(1+0.946194x+0.29808y)
7
(1-0.0144903x+0.36267y)
7
(1-1.85x+0.616442y)
7
(1-0.336689x+0.674633y)
7
(1-1.47936x+0.820191y)
7
(1-0.873239x+1.04232y)
Verifying the candidate ...
Valid interpolant (simplified): 0.327385+1.+(-0.289473-5.67609y)+4.89085+0.577725+(-14.1691-0.857304y+6.04098)+(0.901236+9.10259y-0.269838-5.93363)+(26.4312+1.5065y-21.4473+2.62665+2.5298)+(-0.84717-0.159728y+2.75826-9.4701-1.50527-1.11237)+x(-10.2067-0.616265y-27.9551-1.1172+4.95755-0.168956+0.39194)<0.469264y+4.4762+13.9573+4.12701+0.112326
7
x
6
x
4
y
6
y
5
x
2
y
4
x
2
y
3
y
3
x
2
y
3
y
4
y
2
x
2
y
3
y
4
y
5
y
2
y
3
y
4
y
5
y
6
y
2
y
3
y
5
y
7
y
Improved valid interpolant (rounded under precision 0.01): ++-----+-++--+++-++-+++-+---+x----++<0
1
85
7
x
27
6
x
1
96
y
5
y
59
2
y
6
3
y
2
4
y
6
5
y
7
6
y
48
5
x
1
2
y
32
2
2
y
9
4
x
1
31
y
3
2
3
y
9
3
x
15
16
y
18
10
2
y
13
3
y
10
4
y
11
2
x
1
32
2
y
10
3
y
3
4
y
18
5
y
25
3
8
y
45
2
y
3
y
25
2
4
y
11
6
y
71
Elapsed time: 48.8211
Rendering graphics ...
 |
|
Done.
IJCAR’16-1
IJCAR’16-1
consPhi12=-x1^2+4*x1+x2-4≥0&&-x1-x2+3-y^2>0;consPsi12=-3*x1^2-x2^2+1≥0&&x2-z^2≥0;degree12=1;initialRange12={-2,2};
main[consPhi12,consPsi12,degree12,initialRange12]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 2.92005+3.79198(1+0.439977x1+0.632913x2)-2.32003(1+1.21631x1+0.740265x2)-1.47194(1+0.837402x1+1.39782x2)<0
Verifying the candidate ...
Valid interpolant (simplified): 1.x1+0.576236x2>1.22378
Improved valid interpolant (rounded under precision 0.1): 1--<0
3x1
4
x2
2
Elapsed time: 0.1635
Rendering graphics ...
 |
|
Done.
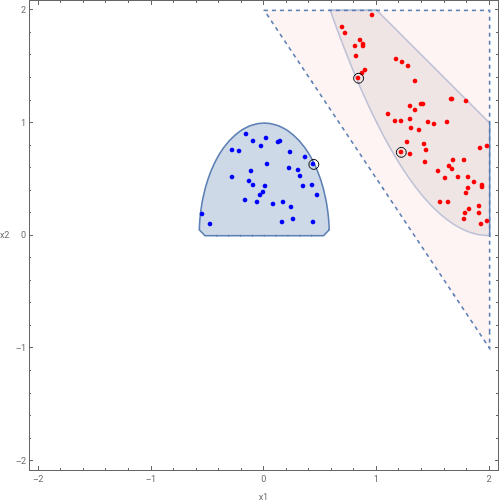
CAV’13-1: From L. Dai et al. [CAV’13: Generating non-linear interpolants by semidefinite programming].
CAV’13-1: From L. Dai et al. [CAV’13: Generating non-linear interpolants by semidefinite programming].
consPhi17=1-a^2-b^2>0&&a^2+b-1-x0&&b+x*b+1-y0;consPsi17=x^2-2*y^2-4>0;degree17=2;initialRange17={-5,5};
main[consPhi17,consPsi17,degree17,initialRange17]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: -0.994921+0.0290539+0.157464-0.186518<0
2
(1+2.01404x+0.123875y)
2
(1-2.26711x+0.647745y)
2
(1-1.5122x+1.26234y)
Verifying the candidate ...
Valid interpolant (simplified): -0.994921-0.0328426x+0.500669-0.259708y+0.264113xy-0.230705<0
2
x
2
y
Improved valid interpolant (rounded under precision 0.1): -1+-+-<0
2
x
2
y
3
xy
3
2
y
4
Elapsed time: 3.25069
Rendering graphics ...
 |
|
Done.
CAV’13-2: From L. Dai et al. [CAV’13].
CAV’13-2: From L. Dai et al. [CAV’13].
consPhi5=x^2+y^2+z^2-2≥0&&1.2x^2+y^2+xz==0;consPsi5=20-3x^2-4y^3-10z^2≥0&&x^2+y^2-z-1==0;degree5=4;initialRange5={-3,3};
main[consPhi5,consPsi5,degree5,initialRange5]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 0.964937-0.0115105-0.00214521+0.0223284+0.0135042-0.0235766+0.000927089+0.000472651<0
4
(1-1.67058x)
4
(1+1.68358x)
4
(1-0.0429159x-0.606061y-0.630849z)
4
(1-0.912404x+0.0243902y-0.166923z)
4
(1-0.784033x+0.37146y+1.11683z)
4
(1+1.19871x+0.845625y+1.15198z)
4
(1+0.226337x-1.71819y+2.00339z)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x0.200387,y-0.886792,z-4.16487},{x0.620155,y0.891892,z-2.02688},{x-0.415268,y-0.552632,z1.23375},{x-1.18627,y-0.345455,z0.526586},{x-0.000174785,y-0.0158622,z1.43974},{x0.351984,y-0.542267,z-1.2578},{x1.44531,y0.771429,z-2.14612},{x0.356872,y-1.1922,z-4.41103},{x-0.22018,y-0.505238,z1.42356},{x-0.350062,y1.35313,z0.953491},{x0.3545,y1.00877,z-3.29598},{x0.337972,y-0.53841,z-1.26329},{x0.324135,y-0.534018,z-1.26876},{x-1.43738,y0.321105,z1.16916},{x-0.00151433,y0.0464806,z1.42848},{x0.346172,y0.540738,z-1.26007},{x0.726009,y-1.24242,z-2.99738},{x0.893338,y0.124206,z-1.08927},{x1.63113,y-0.365399,z-2.03921},{x-0.00100956,y0.0380178,z1.43288},{x0.339883,y1.12821,z-4.15282},{x-0.00346773,y0.0699304,z1.41438},{x-1.46936,y-0.0624165,z1.16292},{x0.787702,y-0.366596,z-1.11586},{x0.347669,y0.541141,z-1.25948},{x1.47155,y-0.99044,z-2.43249},{x0,y0,z1.41448},{x1.63137,y0.530924,z-2.13043},{x-0.24545,y-0.548028,z1.51815},{x-1.231,y-0.92061,z1.3629}}
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: 1.05283-0.00198816-0.0143455-0.0376399+0.0759819+0.0155189-0.0197394+0.00111982-0.0216329+0.00272533<0
4
(1+1.41448x)
4
(1+0.347669x+0.541141y-1.25948z)
4
(1+0.351984x-0.542267y-1.2578z)
4
(1-0.0429159x-0.606061y-0.630849z)
4
(1-1.18627x-0.345455y+0.526586z)
4
(1-0.784033x+0.37146y+1.11683z)
4
(1+1.19871x+0.845625y+1.15198z)
4
(1-0.22018x-0.505238y+1.42356z)
4
(1+0.226337x-1.71819y+2.00339z)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-1.4251,y-0.398873,z1.19001},{x-0.115162,y1.38941,z0.943721},{x-0.121245,y1.38979,z0.946227},{x-0.956539,y1.08851,z1.09983},{x-1.41594,y-0.438006,z1.19672},{x-0.707024,y1.20871,z0.960859},{x-1.4117,y0.422391,z1.17132},{x-1.42877,y0.175182,z1.07207},{x-1.42877,y0.35876,z1.17009},{x-0.187631,y1.38733,z0.959883},{x-0.182412,y1.37084,z0.912469},{x-1.45612,y0.0948276,z1.12929},{x-0.133974,y1.38606,z0.939111},{x-1.1882,y0.859225,z1.15009},{x-0.871556,y1.06733,z0.898796},{x-1.03764,y0.962025,z1.00219},{x-0.956539,y1.05856,z1.03551},{x-1.21149,y-0.935806,z1.34343},{x-1.03764,y1.02079,z1.11871},{x-0.476135,y1.29491,z0.903487},{x-0.607295,y-1.57864,z1.86092},{x-1.45798,y0.200251,z1.1658},{x-0.720217,y-1.50825,z1.79354},{x-1.07567,y-1.16357,z1.51097},{x-1.41144,y-0.45603,z1.20012},{x-1.45186,y-0.253689,z1.17225},{x-0.108967,y1.39281,z0.951806},{x-0.14246,y1.39165,z0.95699},{x-0.493597,y-1.60467,z1.81859},{x-0.194916,y1.38652,z0.960422}}
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant: 0.939928-0.011877-0.0426245+0.0976132+0.0167766+0.0373272-0.0932599-0.00504493+0.00108931<0
4
(1+0.347669x+0.541141y-1.25948z)
4
(1+0.351984x-0.542267y-1.2578z)
4
(1-0.0429159x-0.606061y-0.630849z)
4
(1-0.187631x+1.38733y+0.959883z)
4
(1-1.42877x+0.175182y+1.07207z)
4
(1-0.784033x+0.37146y+1.11683z)
4
(1-0.22018x-0.505238y+1.42356z)
4
(1+0.226337x-1.71819y+2.00339z)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-1.25742,y0.689462,z1.05647},{x-0.859944,y1.09972,z0.948883},{x-1.00868,y0.983931,z0.985562},{x-0.697199,y1.24624,z1.03921},{x-1.15966,y0.822539,z1.02139},{x-0.808683,y1.14274,z0.95983},{x-1.33838,y0.615574,z1.17018},{x-1.16807,y0.884285,z1.14634},{x-1.33165,y0.629599,z1.16969},{x-1.00868,y1.04624,z1.11206},{x-0.847339,y1.16441,z1.07383},{x-0.643697,y1.24255,z0.958273},{x-1.25742,y0.761766,z1.1614},{x-0.572829,y1.29591,z1.00752},{x-0.658824,y1.26365,z1.03086},{x-0.859944,y1.15642,z1.07682},{x-0.697199,y1.20683,z0.942534},{x-1.21625,y0.819071,z1.15013},{x-0.643697,y1.27015,z1.02764},{x-1.13389,y0.882199,z1.06399},{x-1.33838,y0.604857,z1.1571},{x-0.730812,y1.1776,z0.920833},{x-0.814286,y1.18446,z1.06601},{x-0.935014,y1.03337,z0.942106},{x-1.13389,y0.924056,z1.13959},{x-0.969188,y1.06463,z1.07276},{x-0.969188,y1.07865,z1.10282},{x-0.740056,y1.18977,z0.963231},{x-0.838375,y1.16997,z1.0717},{x-0.808683,y1.18774,z1.0647}}
Learning a candidate interpolant at step 4 ...
Synthesized candidate interpolant: 0.794472-0.00869728-0.0496992+0.125332+0.00195602+0.0119537-0.131972+0.00113373+0.0386328+0.0108158+0.00054528<0
4
(1+0.347669x+0.541141y-1.25948z)
4
(1+0.351984x-0.542267y-1.2578z)
4
(1-0.0429159x-0.606061y-0.630849z)
4
(1-0.14246x+1.39165y+0.95699z)
4
(1-0.643697x+1.27015y+1.02764z)
4
(1-0.784033x+0.37146y+1.11683z)
4
(1+1.19871x+0.845625y+1.15198z)
4
(1-1.33165x+0.629599y+1.16969z)
4
(1-1.4251x-0.398873y+1.19001z)
4
(1+0.226337x-1.71819y+2.00339z)
Verifying the candidate ...
Valid interpolant (simplified): 6.63539+1.+0.496759+(-2.09483-0.760297y-2.36367z)+0.0608835+(0.284753+1.26084z)+(2.66558+1.98171z+1.16297)+y(-2.16486+0.596372z-1.30254-1.63679)+(0.452038+1.3399+3.17242z+0.99588+y(1.45747+1.10082z))+x(0.141155-0.647194+(-2.8253-1.34484z)+6.00189z-0.385724+2.42238+y(1.41104-1.82149z+1.60742))<2.61839z+6.05721+1.77051
4
x
4
y
3
x
3
z
3
y
2
y
2
z
2
z
3
z
2
x
2
y
2
z
3
y
2
y
2
z
3
z
2
z
2
z
4
z
Improved valid interpolant (rounded under precision 0.1): ++---+z--++y+++++++y---+x--+++y-+<0
4
3
3
4
4
x
8
3
x
1
3
z
3
z
3
3
y
6
2
2
z
3
4
z
4
2
x
2
y
6
1
5
z
7
z
3
2
z
8
2
y
1
3
z
4
2
z
7
1
3
2
z
6
3
z
5
2
y
1
3
z
6
2z
3
3
z
3
1
5
z
4
2
z
5
Elapsed time: 3857.89
Rendering graphics ...
|
Done.
accelerating: CAV’13-3, from L. Dai et al. [CAV’13].
accelerating: CAV’13-3, from L. Dai et al. [CAV’13].
consPhi17=vc<49.61&&fa0.5418vc^2&&fr1000-fa&&ac0.0005fr&&vc1vc+ac;consPsi17=vc1≥49.61;degree17=1;initialRange17={0,1000};
main[consPhi17,consPsi17,degree17,initialRange17]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: -1.01994-0.000794849(1+0.5vc1)+0.000794849(1+50.6618vc1)<0
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{vc126.9762,ac0.307328,fa385.343,fr614.657,vc26.6689},{vc139.0556,ac0.0886603,fa822.679,fr177.321,vc38.9669},{vc149.2222,ac-0.160635,fa1321.27,fr-321.27,vc49.3829},{vc127.4921,ac0.29969,fa400.621,fr599.379,vc27.1924},{vc134.1587,ac0.187367,fa625.266,fr374.734,vc33.9714},{vc142.4048,ac0.0131802,fa973.64,fr26.3604,vc42.3916},{vc136.8254,ac0.135325,fa729.35,fr270.65,vc36.6901},{vc136.4683,ac0.142532,fa714.937,fr285.063,vc36.3257},{vc127.0556,ac0.306163,fa387.674,fr612.326,vc26.7494},{vc133.381,ac0.201778,fa596.445,fr403.555,vc33.1792},{vc125.581,ac0.327233,fa345.534,fr654.466,vc25.2538},{vc137.2302,ac0.127068,fa745.863,fr254.137,vc37.1031},{vc143.7619,ac-0.0192585,fa1038.52,fr-38.517,vc43.7812},{vc140.2381,ac0.0627516,fa874.497,fr125.503,vc40.1753},{vc129.754,ac0.264416,fa471.168,fr528.832,vc29.4896},{vc147.1587,ac-0.105157,fa1210.31,fr-210.313,vc47.2639},{vc129.1825,ac0.273602,fa452.797,fr547.203,vc28.9089},{vc145.6349,ac-0.0657895,fa1131.58,fr-131.579,vc45.7007},{vc134.6508,ac0.178071,fa643.858,fr356.142,vc34.4727},{vc146.8095,ac-0.0960151,fa1192.03,fr-192.03,vc46.9055},{vc145.6746,ac-0.0667975,fa1133.59,fr-133.595,vc45.7414},{vc135.3413,ac0.164793,fa670.415,fr329.585,vc35.1765},{vc146.9206,ac-0.0989161,fa1197.83,fr-197.832,vc47.0196},{vc135.4444,ac0.162785,fa674.43,fr325.57,vc35.2817},{vc134.3968,ac0.182886,fa634.228,fr365.772,vc34.2139},{vc147.7222,ac-0.120059,fa1240.12,fr-240.117,vc47.8423},{vc141.746,ac0.0285394,fa942.921,fr57.0788,vc41.7175},{vc131.0794,ac0.242396,fa515.208,fr484.792,vc30.837},{vc142.9365,ac0.000597917,fa998.804,fr1.19583,vc42.9359},{vc144.5079,ac-0.0375469,fa1075.09,fr-75.0938,vc44.5455}}
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: -27.925-0.162986(1+47.1587vc1)+0.162986(1+50.6618vc1)<0
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{vc148.9414,ac-0.152937,fa1305.87,fr-305.875,vc49.0943},{vc149.2117,ac-0.160346,fa1320.69,fr-320.692,vc49.3721},{vc149.4393,ac-0.166615,fa1333.23,fr-333.23,vc49.6059},{vc148.9529,ac-0.153253,fa1306.51,fr-306.506,vc49.1062},{vc149.1021,ac-0.157338,fa1314.68,fr-314.675,vc49.2595},{vc149.2867,ac-0.162408,fa1324.82,fr-324.816,vc49.4491},{vc149.1618,ac-0.158975,fa1317.95,fr-317.95,vc49.3208},{vc149.1538,ac-0.158756,fa1317.51,fr-317.511,vc49.3126},{vc148.9432,ac-0.152986,fa1305.97,fr-305.972,vc49.0961},{vc149.0847,ac-0.15686,fa1313.72,fr-313.721,vc49.2416},{vc148.9102,ac-0.152085,fa1304.17,fr-304.171,vc49.0623},{vc149.1709,ac-0.159224,fa1318.45,fr-318.448,vc49.3301},{vc149.3171,ac-0.163244,fa1326.49,fr-326.489,vc49.4803},{vc149.2382,ac-0.161074,fa1322.15,fr-322.148,vc49.3993},{vc149.0036,ac-0.154637,fa1309.27,fr-309.275,vc49.1582},{vc149.3931,ac-0.16534,fa1330.68,fr-330.68,vc49.5584},{vc148.9908,ac-0.154287,fa1308.57,fr-308.575,vc49.1451},{vc149.359,ac-0.1644,fa1328.8,fr-328.799,vc49.5234},{vc149.1131,ac-0.15764,fa1315.28,fr-315.279,vc49.2708},{vc149.3853,ac-0.165125,fa1330.25,fr-330.249,vc49.5504},{vc149.3599,ac-0.164424,fa1328.85,fr-328.848,vc49.5243},{vc149.1286,ac-0.158063,fa1316.13,fr-316.127,vc49.2867},{vc149.3877,ac-0.165193,fa1330.39,fr-330.386,vc49.5529},{vc149.1309,ac-0.158127,fa1316.25,fr-316.254,vc49.289},{vc149.1075,ac-0.157484,fa1314.97,fr-314.967,vc49.2649},{vc149.4057,ac-0.165688,fa1331.38,fr-331.376,vc49.5714},{vc149.2719,ac-0.162002,fa1324.,fr-324.004,vc49.4339},{vc149.0332,ac-0.155449,fa1310.9,fr-310.898,vc49.1887},{vc149.2986,ac-0.162736,fa1325.47,fr-325.471,vc49.4613},{vc149.3337,ac-0.163704,fa1327.41,fr-327.409,vc49.4975}}
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant: -81.8759-1.33812(1+49.4393vc1)+1.33812(1+50.6618vc1)<0
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{vc149.7686,ac2.,fa1.3,fr3.6,vc-1.},{vc149.6373,ac0.1,fa0.8,fr-1.9,vc-1.4},{vc149.9809,ac-0.4,fa3.3,fr-2.5,vc-3.6},{vc150.0047,ac0.9,fa4.4,fr4.,vc-5.},{vc149.8114,ac4.9,fa-5.,fr-4.,vc-0.1},{vc149.9212,ac-1.6,fa2.8,fr2.4,vc4.4},{vc150.0091,ac1.6,fa-4.1,fr3.4,vc-2.},{vc149.7924,ac1.5,fa-1.1,fr4.2,vc2.2},{vc149.931,ac3.6,fa-4.5,fr1.1,vc3.1},{vc149.9817,ac-4.,fa-0.4,fr-2.8,vc3.3},{vc149.7543,ac-4.3,fa-4.4,fr3.1,vc-3.4},{vc149.9463,ac-3.4,fa-2.4,fr-4.7,vc-4.2},{vc149.7117,ac3.7,fa0.2,fr-4.5,vc4.6},{vc149.6453,ac0.4,fa-0.1,fr-1.4,vc1.3},{vc149.8592,ac0.7,fa-1.9,fr-3.8,vc1.9},{vc149.6872,ac-4.7,fa4.7,fr1.7,vc-0.4},{vc149.773,ac0.4,fa-3.2,fr-5.,vc2.8},{vc149.7777,ac0.1,fa-2.,fr-3.3,vc0.2},{vc149.6766,ac3.2,fa-2.7,fr-3.3,vc4.2},{vc149.8811,ac3.4,fa-0.8,fr-4.,vc4.4},{vc150.0473,ac-0.1,fa0.4,fr2.3,vc1.4},{vc149.6358,ac3.3,fa1.2,fr-2.3,vc2.9},{vc149.818,ac4.5,fa-0.8,fr-4.4,vc-0.3},{vc150.0195,ac-1.1,fa3.2,fr4.3,vc-3.5},{vc149.8445,ac-0.1,fa-3.6,fr2.2,vc-0.2},{vc149.7905,ac-1.9,fa0.7,fr3.1,vc1.},{vc149.9601,ac4.3,fa4.,fr-4.2,vc3.1},{vc149.61,ac-4.4,fa-3.4,fr2.,vc1.9},{vc149.909,ac1.1,fa3.5,fr-4.9,vc1.9},{vc149.8255,ac2.6,fa4.3,fr4.7,vc-4.8}}
Learning a candidate interpolant at step 4 ...
Synthesized candidate interpolant: -582.126-68.8403(1+49.4393vc1)+68.8403(1+49.61vc1)<0
Verifying the candidate ...
Valid interpolant (simplified): 1.vc1<49.5249
Improved valid interpolant (rounded under precision 0.0001): -1+<0
2vc1
99
Elapsed time: 40.6298
Done.
Benchmark B: parallel/sharp/adjacent cases where numerical issues make trouble, however being well-addressed by the rounding (rational recovery) effect.
Benchmark B: parallel/sharp/adjacent cases where numerical issues make trouble, however being well-addressed by the rounding (rational recovery) effect.
Parallel_parabola
Parallel_parabola
consPhi6=y-x^2-1≥0;consPsi6=y-x^2<0;degree6=2;initialRange6={-5,5};
main[consPhi6,consPsi6,degree6,initialRange6]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 0.907911+1.8922-2.33295+0.698649-0.443016+0.185107<0
2
(1+0.722374x+0.512151y)
2
(1+0.53848x+1.31544y)
2
(1-1.57577x+2.46792y)
2
(1-1.43783x+3.08982y)
2
(1+2.09897x+4.34937y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:x-,y,x-,y-,x-,y-,x-,y-,x,y-,x,y2620,x,y-,x,y-3676,x-,y-,x-,y-,x-,y-,x-,y-,x-,y,x-193,y,x-,y-,x-130,y-,x-,y2482,x,y,x,y,x-,y-,x,y,x-,y,x,y,x,y-,x-,y-,x-,y-,x46,y-,x,y,x-,y-,x,y
373
10
10687
10
1713
10
15797
5
1018
5
16659
5
393
10
2884
5
119
10
14359
10
385
2
541
5
16538
5
242
5
739
5
16553
5
897
10
19367
10
898
5
11029
5
17
5
6137
10
847
5
30899
10
13824
5
1326
5
18703
5
28629
10
849
5
1631
10
5993
2
957
10
5904
5
7
2
14716
5
249
10
3061
5
873
5
12297
5
391
5
9133
5
1029
5
34027
10
273
10
7347
10
331
10
4593
10
3317
2
739
5
18691
10
1633
10
11393
5
1443
10
34853
10
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: 0.983029+1.60978-2.11287+0.919548-0.674351+0.257888+4.23387×<0
2
(1+0.722374x+0.512151y)
2
(1+0.53848x+1.31544y)
2
(1-1.57577x+2.46792y)
2
(1-1.43783x+3.08982y)
2
(1+1.76827x+3.10385y)
-6
10
2
(1+24.9x+612.2y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x15.0198,y27316.1},{x-39.0889,y1593.},{x2901.,y8.4158×},{x82.0727,y6736.93},{x-55.0889,y3061.},{x638.,y407096.},{x3007.,y9.04205×},{x2675.,y7.15566×},{x-1556.,y2.42114×},{x26.0792,y27251.1},{x37.4563,y27214.},{x812.,y659369.},{x-74.4357,y5541.68},{x37.1695,y26927.4},{x-1264.,y1.59776×},{x-208.,y43265.},{x66.5273,y4426.88},{x9.54455,y90.5588},{x-47.8,y2718.05},{x37.4104,y26917.2},{x-74.0222,y13573.5},{x-7.61177,y29239.},{x-7.61177,y29028.},{x3.15049,y27115.9},{x37.4104,y26998.},{x-62.4,y3894.76},{x-2928.,y8.57323×},{x-2928.,y8.57319×},{x14.,y27309.8},{x-36.1333,y24313.9}}
6
10
6
10
6
10
6
10
6
10
6
10
6
10
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant (rounded under precision 0.1): +-y<0
1
2
2
x
Verifying the candidate ...
Valid interpolant (simplified): +<y
1
2
2
x
Elapsed time: 4.49543
Rendering graphics ...
 |
|
Done.
Parallel_halfplane
Parallel_halfplane
consPhi7=y-x-1≥0;consPsi7=y-x+1<0;degree7=1;initialRange7={-5,5};
main[consPhi7,consPsi7,degree7,initialRange7]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: -0.0029862+0.695357(1-0.144424x-1.15372y)-0.986762(1+0.115534x+1.11884y)+0.291405(1+4.14368x+3.13179y)<0
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-4121.,y-4118.51},{x4009.,y4007.86},{x3123.,y3121.37},{x-3188.,y-3186.08},{x1940.,y1939.},{x-2851.,y-2850.},{x3469.,y3467.17},{x-4000.,y-3999.},{x2598.,y2596.85},{x-3260.,y-3258.44},{x-1853.,y-1851.88},{x-1887.,y-1886.},{x-2851.,y-2849.52},{x-4482.,y-4481.},{x-3518.,y-3516.04},{x3156.,y3154.37},{x-1858.,y-1857.},{x-3600.,y-3597.83},{x-4482.,y-4480.62},{x-4482.,y-4479.3},{x-3188.,y-3187.},{x-3489.,y-3488.},{x-2002.,y-2000.82},{x-3136.,y-3134.11},{x-3661.,y-3660.},{x-2851.,y-2849.28},{x-1795.,y-1793.93},{x-3282.,y-3280.02},{x-2195.,y-2193.8},{x-3190.,y-3188.59}}
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: -0.00297762+0.986872(1-0.144424x-1.15372y)-0.987517(1+0.115534x+1.11884y)+0.000644515(1+1940x+1939.y)<0
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-264911.,y-264912.},{x267605.,y267606.},{x267019.,y267020.},{x265767.,y265768.},{x266696.,y266697.},{x266063.,y266064.},{x267120.,y267121.},{x-264894.,y-264895.},{x266883.,y266884.},{x265481.,y265482.},{x266628.,y266629.},{x266383.,y266384.},{x266177.,y266178.},{x-265514.,y-265515.},{x265069.,y265070.},{x267108.,y267109.},{x266567.,y266568.},{x-263429.,y-263430.},{x-265331.,y-265332.},{x-265295.,y-265296.},{x265715.,y265716.},{x265069.,y265070.},{x266350.,y266351.},{x266063.,y266064.},{x-263636.,y-263637.},{x266177.,y266178.},{x266681.,y266682.},{x265195.,y265196.},{x266183.,y266184.},{x265715.,y265716.}}
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant (rounded under precision 0.1): x-y<0
Verifying the candidate ...
Valid interpolant (simplified): x<y
Elapsed time: 2.45773
Rendering graphics ...
 |
|
Done.
Sharper-1:
From T. Okudono et al. [APLAS’17: Sharper and simpler nonlinear interpolants for program verification].
Their result: 34y^2 − 68 y − 102 > 0, ours: 2y-y-2>0.
Sharper-1:
From T. Okudono et al. [APLAS’17: Sharper and simpler nonlinear interpolants for program verification].
Their result: 34y^2 − 68 y − 102 > 0, ours:-y-2>0.
From T. Okudono et al. [APLAS’17: Sharper and simpler nonlinear interpolants for program verification].
Their result: 34y^2 − 68 y − 102 > 0, ours:
2
y
consPhi8=y+1<0;consPsi8=x^2+y^2-1≤0;degree8=2;initialRange8={-5,5};
main[consPhi8,consPsi8,degree8,initialRange8]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 5.52694-7.52526+7.52526<0
2
(1-1.00866y)
2
(1-0.782785y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{y-0.949169,x-0.314766},{y-0.907593,x0.419851},{y-0.96092,x0.0546448},{y-0.96092,x-0.276826},{y-0.949402,x0.314062},{y-0.973936,x-0.226825},{y-0.952998,x0.173653},{y-0.90453,x-0.426409},{y-0.967844,x-0.251551},{y-0.981958,x-0.0410448},{y-0.967844,x0.251551},{y-0.907593,x-0.419851},{y-0.96092,x0.276826},{y-0.993975,x-0.109608},{y-0.953297,x0.047619},{y-0.90453,x0.426409},{y-0.99737,x0.0703013},{y-0.908525,x-0.0247934},{y-0.953297,x-0.302034},{y-0.981958,x-0.189099},{y-0.955394,x-0.0175439},{y-1.,x0},{y-0.955394,x0.295333},{y-0.995073,x0.099141},{y-0.952998,x-0.302978},{y-0.991611,x0.0588235},{y-0.966646,x-0.256118},{y-0.908525,x-0.41783},{y-0.964615,x-0.263662},{y-0.91192,x0.282258}}
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: 83.3081-1000-1000+1000+1000<0
2
(1-1.00937y)
2
(1-1.00866y)
2
(1-y)
2
(1-0.99737y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{y-1.0021,x4.2},{y-1.00264,x2.7},{y-1.0035,x4.1},{y-1.00218,x4.},{y-1.00051,x2.9},{y-1.00226,x1.1},{y-1.00427,x-0.2},{y-1.00237,x1.},{y-1.00228,x3.5},{y-1.0026,x1.2},{y-1.00285,x0},{y-1.00217,x-2.8},{y-1.00231,x1.7},{y-1.00316,x2.3},{y-1.00333,x3.6},{y-1.00036,x-0.3},{y-1.00392,x4.5},{y-1.00416,x2.9},{y-1.00276,x-3.7},{y-1.00211,x-4.7},{y-1.00027,x-1.1},{y-1.00402,x0.8},{y-1.0029,x4.9},{y-1.00028,x-2.},{y-1.00169,x1.},{y-1.00049,x-0.6},{y-1.00032,x1.8},{y-1.00019,x-0.3},{y-1.0023,x-2.2},{y-1.00076,x3.7}}
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant (rounded under precision 0.1): 1+-<0
y
2
2
y
2
Verifying the candidate ...
Valid interpolant (simplified): 2+y<
2
y
Elapsed time: 2.19135
Done.
Sharper-2: From T. Okudono et al. [ APLAS’17].
Their result: 8 y + 4 x^2 > 0, ours: y>0.
Sharper-2: From T. Okudono et al. [ APLAS’17].
Their result: 8 y + 4 x^2 > 0, ours:.
Their result: 8 y + 4 x^2 > 0, ours:
y>0
consPhi9=y-x>0&&x+y>0;consPsi9=y+x^2≤0;degree9=2;initialRange9={-5,5};
main[consPhi9,consPsi9,degree9,initialRange9]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 0.698165+6.35104-5.62997-0.721069<0
2
(1+0.0686465x-0.064659y)
2
(1+0.116488x+0.32185y)
2
(1-0.14208x+0.339649y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-1618.,y-2.61799×},{x-0.0765118,y0.105089},{x-0.0355584,y-84.},{x1959.,y-3.83775×},{x2435.,y-5.9293×},{x3.09721,y-2416.},{x0.0309847,y-51.},{x0.114048,y-64.},{x2.12846,y-67.},{x3.09721,y-2943.},{x3.09721,y-538.},{x-536.,y-287296.},{x-0.0879396,y0.14392},{x-0.0678797,y-62.},{x3.09721,y-2010.},{x-0.125362,y-90.},{x1.14822,y-95.},{x0.127834,y0.131547},{x-0.0326647,y0.140819},{x-0.0385992,y0.138071},{x-0.02982,y0.140658},{x-0.133013,y0.142478},{x762.,y-580644.},{x-2.02208,y-106.},{x-0.0460542,y0.141575},{x-0.543375,y-22.},{x2419.,y-5.85156×},{x-2.17114,y-21.},{x-0.133013,y0.146412},{x2.31719,y-10.}}
6
10
6
10
6
10
6
10
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant (rounded under precision 1.): -y<0
Verifying the candidate ...
Valid interpolant (simplified): y>0
Elapsed time: 2.38085
Rendering graphics ...
 |
|
Done.
Sharper-3: From T. Okudono et al. [ APLAS’17].
Sharper-3: From T. Okudono et al. [ APLAS’17].
In[]:=
consPhi20=x^2+(y-1)^2<1;consPsi20=x^2+(y-2)^2≥4;degree20=2;initialRange20={-3,3};
In[]:=
main[consPhi20,consPsi20,degree20,initialRange20]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 0.974225+967.36+82.89-1055.28+1.82619+2.56437+0.643779<0
2
(1-0.201241x-0.000747645y)
2
(1-0.339761x+0.0113412y)
2
(1-0.219038x+0.035215y)
2
(1-1.53175x+0.647677y)
2
(1-2.01155x+1.95088y)
2
(1+1.85836x+2.77648y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-1.85427,y1.23157},{x-1.78371,y1.07195},{x-1.72558,y0.966283},{x-1.59775,y0.797006},{x-0.968975,y3.76378},{x0.20026,y4.01346},{x0.578035,y3.91465},{x1.56069,y3.25774},{x-0.876655,y3.80026},{x-1.64667,y0.857657},{x-0.541052,y3.93794},{x-0.932652,y3.79598},{x-0.876655,y3.79763},{x0.347204,y0.0655942},{x-1.25047,y3.56952},{x0.190414,y0.0365879},{x-0.339009,y3.9798},{x0.194873,y4.05587},{x0.00575887,y0.0172008},{x0.740366,y3.85792},{x0.364481,y0.0713664},{x-0.178158,y3.99205},{x-1.57644,y0.769219},{x-0.254229,y3.98378},{x-1.59724,y0.796327},{x-1.53792,y0.716529},{x-0.612183,y0.0959958},{x0.00575887,y0.000850629},{x-1.88205,y1.32333},{x-1.47181,y0.632387}}
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: -0.940373+1000+1000-1791.51-126.688-80.4038-2.78949+1.3897<0
2
(1+0.209925x-0.00715669y)
2
(1-0.201241x-0.000747645y)
2
(1+0.00575887x+0.000850629y)
2
(1+0.364481x+0.0713664y)
2
(1-0.623891x+0.224801y)
2
(1+0.763088x+0.367216y)
2
(1-0.541052x+3.93794y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x0.190823,y0.00912414},{x-0.0473715,y-0.00674974},{x-0.173894,y0.00757409},{x-0.0882091,y0.00194616},{x-0.108999,y-0.00531428},{x0.184289,y0.00850868},{x-0.00950401,y-0.00156829},{x-0.0233145,y0.000135896},{x0.027324,y-0.00132372},{x-0.0647461,y-0.00824242},{x0.156222,y-0.000495197},{x-0.0579151,y-0.00262041},{x0.138699,y0.00481516},{x-0.0882091,y-0.00865847},{x0.0582121,y-0.00231548},{x0.187853,y0.00378463},{x-0.169439,y0.00657652},{x0.0960796,y-0.00241319},{x0.157262,y0.00619239},{x0.174636,y0.00763904},{x-0.108999,y0.00297241},{x0.229433,y0.0132034},{x0.13172,y0.00434223},{x0.13172,y-0.00301694},{x0.0503416,y0.000633668},{x-0.0473715,y0.000561095},{x-0.0647461,y0.00104829},{x0.242501,y0.0140606},{x0.175379,y0.00770426},{x-0.0847936,y0.0017983}}
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant (rounded under precision 0.1): -y+<0
2
x
2
2
y
3
Verifying the candidate ...
Valid interpolant (simplified): 3+2(-3+y)y<0
2
x
Elapsed time: 2.91455
Rendering graphics ...
 |
|
Done.
Sharper-4: From T. Okudono et al. [ APLAS’17].
Sharper-4: From T. Okudono et al. [ APLAS’17].
In[]:=
consPhi20=x^2+(y-1)^2<1;consPsi20=x^2+(y+1)^2≤1;degree20=1;initialRange20={-3,3};
In[]:=
main[consPhi20,consPsi20,degree20,initialRange20]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: -0.579427+386.712(1-0.226317x-0.0727238y)+511.802(1+0.101396x-0.0220103y)-898.514(1-0.0468636x+0.00278714y)<0
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x0.0152007,y-0.000115537},{x-0.221517,y-0.0377793},{x-0.347255,y-0.0622293},{x-0.262102,y-0.0349597},{x-0.282763,y-0.055814},{x0.0087072,y-0.0000379084},{x-0.183884,y-0.019985},{x-0.197609,y-0.0197191},{x-0.147285,y-0.0134929},{x-0.238784,y-0.0454349},{x-0.0191854,y-0.0111861},{x-0.231995,y-0.0333407},{x-0.0365998,y-0.000669996},{x-0.262102,y-0.0540593},{x-0.116588,y-0.0121528},{x0.0122491,y-0.00833725},{x-0.342828,y-0.0617614},{x-0.0789551,y-0.0111212},{x-0.0181523,y-0.000164767},{x-0.000885478,y-3.92036×},{x-0.282763,y-0.0408101},{x0.0535714,y-0.00143598},{x-0.043536,y-0.000948142},{x-0.043536,y-0.013209},{x-0.12441,y-0.00776906},{x-0.221517,y-0.0248435},{x-0.238784,y-0.0289273},{x0.0665584,y-0.00334335},{x-0.00014758,y-1.08899×},{x-0.258707,y-0.0340442}}
-7
10
-8
10
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant (rounded under precision 1.): -y<0
Verifying the candidate ...
Valid interpolant (simplified): y>0
Elapsed time: 0.961523
Rendering graphics ...
 |
|
Done.
Adjacent-1
Adjacent-1
consPhi15=x+y>0||x+y<0;consPsi15=x+y0;degree15=2;initialRange15={-5,5};
main[consPhi15,consPsi15,degree15,initialRange15]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant (rounded under precision 0.1): --xy-<0
2
x
2
2
y
2
Verifying the candidate ...
Valid interpolant (simplified): >0
2
(x+y)
Elapsed time: 0.183805
Rendering graphics ...
 |
|
Done.
Adjacent-2
Adjacent-2
consPhi10=y-x^2>0;consPsi10=y-x^2≤0;degree10=2;initialRange10={-5,5};
main[consPhi10,consPsi10,degree10,initialRange10]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant (rounded under precision 0.1): -y<0
2
x
Verifying the candidate ...
Valid interpolant (simplified): <y
2
x
Elapsed time: 0.251797
Rendering graphics ...
 |
|
Done.
IJCAR’16-2
IJCAR’16-2
consPhi11=-y1+x1-2≥0&&2*x2-x1-1>0&&-y1^2-x1^2+2*x1*y1-2*y1+2*x1≥0&&-y2^2-y1^2-x2^2-4*y1+2*x2-4≥0;consPsi11=-z1+2*x2+1≥0&&2*x1-x2-1>0&&-z1^2-4*x2^2+4*x2*z1+3*z1-6*x2-2≥0&&-z2^2-x1^2-x2^2+2*x1+z1-2*x2-1≥0;degree11=1;initialRange11={-3,3};
main[consPhi11,consPsi11,degree11,initialRange11]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: -0.266009+3.90077(1+0.923065x1+0.4x2)+3.39763(1+1.45522x1+0.89038x2)-7.2984(1+0.816059x1+1.01325x2)<0
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x11.07396,x20.935223,y11.2,y24.9,z12.87045,z20.346249},{x11.08776,x20.923818,y10,y21.9,z12.84764,z2-0.372639},{x11.0747,x20.940704,y13.4,y2-0.3,z12.88141,z20.104575},{x11.09909,x20.958873,y10.4,y24.2,z12.91775,z20.265978},{x10.868646,x20.722309,y10.1,y2-2.,z12.44462,z2-0.226667},{x11.10739,x20.936992,y1-4.,y20.1,z12.87398,z20.164474},{x10.890209,x20.769648,y10.5,y2-2.,z12.5393,z20.246914},{x11.08776,x20.923818,y10.4,y2-3.8,z12.84764,z2-0.25},{x10.956929,x20.900878,y1-0.8,y21.7,z12.80176,z20.401709},{x10.937025,x20.770833,y12.5,y23.8,z12.54167,z20.633917},{x11.05868,x20.970964,y10.1,y23.3,z12.94193,z20.231918},{x10.956929,x20.900878,y11.4,y2-1.7,z12.80176,z20.43193},{x10.936383,x20.817805,y1-0.6,y2-1.,z12.63561,z20.247191},{x11.05868,x20.970964,y14.9,y24.6,z12.94193,z2-0.087156},{x11.02416,x20.994039,y1-4.7,y2-0.4,z12.98808,z2-0.0968421},{x10.961958,x20.793464,y14.,y21.5,z12.58693,z20.309524},{x11.12262,x20.992454,y14.4,y24.7,z12.98491,z20},{x10.93847,x20.795983,y14.2,y2-3.,z12.59197,z20.464286},{x11.0798,x20.976145,y1-2.7,y24.6,z12.95229,z20.201923},{x11.06726,x20.939655,y1-4.2,y2-3.6,z12.87931,z2-0.335446},{x11.01391,x20.984152,y1-5.,y2-1.1,z12.9683,z2-0.0769231},{x10.933868,x20.828629,y1-2.,y2-0.6,z12.65726,z20.555878},{x11.01322,x20.880573,y12.3,y24.6,z12.76115,z20.473726},{x10.966667,x20.880435,y10.1,y23.1,z12.76087,z20.472994},{x11.02616,x20.999658,y11.1,y2-2.5,z12.99932,z20},{x10.997271,x20.959596,y12.9,y20.4,z12.91919,z20.281368},{x10.980738,x20.894419,y14.5,y24.8,z12.78884,z2-0.446814},{x11.10739,x20.936992,y1-2.4,y2-4.1,z12.87398,z2-0.332436},{x11.15605,x20.975072,y1-4.3,y23.7,z12.95014,z20.157745},{x11.16607,x20.986115,y14.7,y2-2.,z12.97223,z20}}
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: -3.3169+11.4186(1+0.890209x1+0.769648x2)+47.5228(1+0.997271x1+0.959596x2)-58.9414(1+0.816059x1+1.01325x2)<0
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x10.995988,x21.08948,y1-1.00401,y20,z1-3.,z20.9},{x10.993236,x21.11611,y1-1.00676,y20,z11.2,z24.3},{x10.990761,x21.02164,y1-1.00924,y20.0793651,z13.4,z24.3},{x10.988154,x21.11653,y1-1.01185,y2-0.0998589,z1-0.1,z2-3.1},{x10.997291,x21.07356,y1-1.00271,y20,z1-3.5,z20.9},{x10.990761,x21.09566,y1-1.00924,y2-0.0961404,z12.1,z2-3.3},{x10.990841,x21.13504,y1-1.00916,y20,z11.,z20.9},{x10.898925,x20.96252,y1-1.10107,y20.436495,z1-1.1,z2-3.7},{x10.945429,x20.980408,y1-1.05457,y20.0769231,z1-2.1,z23.7},{x10.999009,x21.04452,y1-1.00099,y20,z13.6,z2-0.7},{x10.968863,x21.01111,y1-1.03114,y2-0.247346,z13.9,z20.9},{x10.997635,x21.04152,y1-1.00236,y20.054766,z1-4.5,z24.9},{x10.990761,x21.03047,y1-1.00924,y2-0.132156,z10.3,z23.9},{x10.989584,x21.13354,y1-1.01042,y20.0537643,z1-1.6,z2-3.8},{x10.990761,x21.0529,y1-1.00924,y2-0.017284,z1-1.3,z24.8},{x10.99605,x21.02066,y1-1.00395,y20.0478632,z11.9,z2-2.},{x10.935123,x20.990391,y1-1.06488,y20.174825,z11.2,z2-1.4},{x10.935123,x20.990391,y1-1.06488,y20.354193,z1-5.,z23.},{x10.896872,x20.96062,y1-1.10313,y2-0.440534,z1-2.7,z2-3.4},{x10.945319,x20.97392,y1-1.05468,y20.325104,z1-4.8,z20.6},{x10.922874,x21.01518,y1-1.07713,y2-0.384803,z1-0.9,z20.3},{x10.988154,x21.11653,y1-1.01185,y20.0750988,z1-2.9,z2-2.5},{x10.900722,x20.956555,y1-1.09928,y2-0.00854701,z12.3,z2-3.2},{x10.992811,x21.03415,y1-1.00719,y20.0272109,z14.5,z2-0.8},{x10.949169,x21.01986,y1-1.05083,y20.314139,z10,z21.7},{x10.999781,x21.00479,y1-1.00022,y2-0.00282031,z10.1,z2-2.},{x10.951847,x21.06658,y1-1.04815,y20.299257,z1-0.7,z25.},{x10.997986,x21.06343,y1-1.00201,y20,z1-4.9,z2-2.4},{x10.990761,x21.13562,y1-1.00924,y20,z1-22.3,z213.9},{x10.992811,x21.03415,y1-1.00719,y20.114718,z12.2,z20.8}}
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant: 2.31052+422.045(1+0.997271x1+0.959596x2)-93.3619(1+0.945319x1+0.97392x2)+1000(1+1.02416x1+0.994039x2)-1000(1+0.999781x1+1.00479x2)-328.683(1+0.99605x1+1.02066x2)<0
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x11.00316,x20.99762,y11.2,y24.9,z12.99524,z20.0688757},{x11.00375,x20.997263,y10,y21.9,z12.99453,z2-0.0738468},{x11.00319,x20.997829,y13.4,y2-0.3,z12.99566,z20.0208333},{x11.00424,x20.99863,y10.4,y24.2,z12.99726,z20.0521541},{x10.994846,x20.989092,y10.1,y2-2.,z12.97818,z2-0.0494186},{x11.00459,x20.997851,y1-4.,y20.1,z12.9957,z20.0323415},{x10.995692,x20.990978,y10.5,y2-2.,z12.98196,z20.0530504},{x11.00375,x20.997263,y10.4,y2-3.8,z12.99453,z2-0.0497076},{x10.99831,x20.99611,y1-0.8,y21.7,z12.99222,z20.0818815},{x10.997529,x20.991003,y12.5,y23.8,z12.98201,z20.133818},{x11.00251,x20.998935,y10.1,y23.3,z12.99787,z20.0460654},{x10.99831,x20.99611,y11.4,y2-1.7,z12.99222,z20.088099},{x10.997504,x20.99285,y1-0.6,y2-1.,z12.9857,z20.0518868},{x11.00251,x20.998935,y14.9,y24.6,z12.99787,z2-0.01732},{x11.00103,x20.999769,y1-4.7,y2-0.4,z12.99954,z2-0.0195661},{x10.998507,x20.991887,y14.,y21.5,z12.98377,z20.0678392},{x11.00524,x20.999986,y14.4,y24.7,z12.99997,z20},{x10.997586,x20.99199,y14.2,y2-3.,z12.98398,z20.0975},{x11.00341,x20.999206,y1-2.7,y24.6,z12.99841,z20.0396988},{x11.00288,x20.997786,y1-4.2,y2-3.6,z12.99557,z2-0.0664486},{x11.00059,x20.999381,y1-5.,y2-1.1,z12.99876,z2-0.0153097},{x10.997405,x20.993272,y1-2.,y2-0.6,z12.98654,z20.115772},{x11.00057,x20.995341,y12.3,y24.6,z12.99068,z20.0964182},{x10.998692,x20.995308,y10.1,y23.1,z12.99062,z20.0967468},{x11.00112,x20.999999,y11.1,y2-2.5,z13.,z20},{x10.999893,x20.998413,y12.9,y20.4,z12.99683,z20.056323},{x10.999244,x20.995855,y14.5,y24.8,z12.99171,z2-0.0909514},{x11.00459,x20.997851,y1-2.4,y2-4.1,z12.9957,z2-0.0653688},{x11.00667,x20.999517,y1-4.3,y23.7,z12.99903,z20.0303413},{x11.0071,x20.999975,y14.7,y2-2.,z12.99995,z20}}
Learning a candidate interpolant at step 4 ...
Synthesized candidate interpolant (rounded under precision 0.1): x1-x2<0
Verifying the candidate ...
Valid interpolant (simplified): x1<x2
Elapsed time: 12.3315
Rendering graphics ...
 |
|
Done.
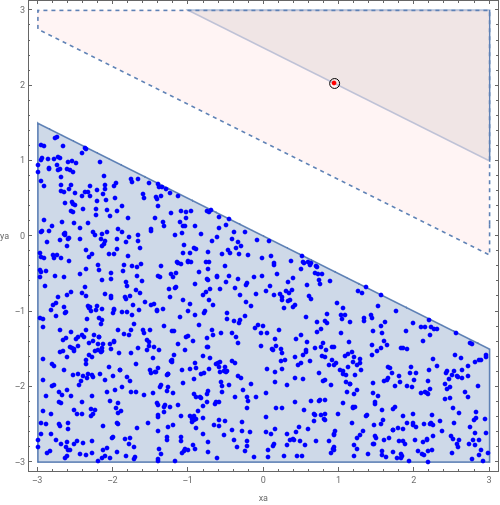
ex1: CAV’13-4, from L. Dai et al. [CAV’13].
Their result: 716.77+1326.74 ya+ 1.33 ya^2 + 433.90 ya^3 + 668.16 xa − 155.86 xa ya + 317.29xa ya^2 + 222.00 xa^2 + 592.39 xa^2 ya + 271.11 xa^3 > 0;
Ours: 2 xa + 4 ya > 5.
ex1: CAV’13-4, from L. Dai et al. [CAV’13].
Their result: 716.77+1326.74 ya+ 1.33 ya^2 + 433.90 ya^3 + 668.16 xa − 155.86 xa ya + 317.29xa ya^2 + 222.00 xa^2 + 592.39 xa^2 ya + 271.11 xa^3 > 0;
Ours: 2 xa + 4 ya > 5.
Their result: 716.77+1326.74 ya+ 1.33 ya^2 + 433.90 ya^3 + 668.16 xa − 155.86 xa ya + 317.29xa ya^2 + 222.00 xa^2 + 592.39 xa^2 ya + 271.11 xa^3 > 0;
Ours: 2 xa + 4 ya > 5.
consPhi18=xa1+2ya1≥0&&xa1+2ya1-x10&&-2xa1+ya1-y10&&x-x1-10&&yy1+x&&xax-2y&&ya2x+y;consPsi18=xa+2ya<0;degree18=1;initialRange18={-3,3};
main[consPhi18,consPsi18,degree18,initialRange18]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 0.998233+0.124133(1+1.3595xa-0.680698ya)+0.275144(1-0.69718xa+0.345733ya)-0.399276(1+0.941647xa+2.02918ya)<0
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{xa-3582.,ya1789.61,x1.,x1-3.6,xa1-4.2,y-2.3,y1-4.5,ya10.2},{xa3489.,ya-1741.9,x1.03922,x10.0392157,xa1698.016,y-1743.98,y1-1745.02,ya1-348.988},{xa1523.,ya-758.837,x1.06516,x10.0651554,xa1304.826,y-760.967,y1-762.033,ya1-152.38},{xa-1593.,ya796.379,x-3.2,x13.3,xa13.7,y-4.6,y10.4,ya13.5},{xa-1568.,ya783.821,x1.5,x12.8,xa10.8,y-0.7,y1-3.6,ya11.9},{xa2140.,ya-1067.5,x1.,x10,xa1428.2,y-1069.5,y1-1070.5,ya1-214.1},{xa2163.,ya-1078.78,x1.08955,x10.0895522,xa1432.836,y-1080.96,y1-1082.04,ya1-216.373},{xa3574.,ya-1782.43,x1.82707,x10.827072,xa1715.331,y-1786.09,y1-1787.91,ya1-357.252},{xa-2560.,ya1279.62,x1.8,x11.6,xa10,y2.9,y13.,ya12.9},{xa-2280.,ya1139.79,x-2.4,x11.2,xa10.1,y0.6,y1-2.3,ya12.5},{xa1414.,ya-704.5,x1.,x10,xa1283.,y-706.5,y1-707.5,ya1-141.5},{xa-1479.,ya739.455,x0,x13.9,xa1-0.1,y1.5,y1-2.,ya1-0.5},{xa2292.,ya-1143.5,x1.,x10,xa1458.6,y-1145.5,y1-1146.5,ya1-229.3},{xa-1774.,ya886.898,x-1.3,x13.4,xa1-0.7,y0,y1-4.8,ya1-3.1},{xa3593.,ya-1792.76,x1.49796,x10.497959,xa1718.999,y-1795.75,y1-1797.25,ya1-359.251},{xa1632.,ya-813.5,x1.,x10,xa1326.6,y-815.5,y1-816.5,ya1-163.3},{xa1439.,ya-717.,x1.,x10,xa1288.,y-719.,y1-720.,ya1-144.},{xa2916.,ya-1455.5,x1.,x10,xa1583.4,y-1457.5,y1-1458.5,ya1-291.7},{xa2859.,ya-1427.,x1.,x10,xa1572.,y-1429.,y1-1430.,ya1-286.},{xa3489.,ya-1740.01,x1.7955,x10.795496,xa1698.318,y-1743.6,y1-1745.4,ya1-348.761},{xa1557.,ya-776.,x1.,x10,xa1311.6,y-778.,y1-779.,ya1-155.8},{xa3502.,ya-1746.5,x1.80032,x10.800325,xa1700.92,y-1750.1,y1-1751.9,ya1-350.06},{xa3773.,ya-1881.75,x1.901,x10.900997,xa1755.16,y-1885.55,y1-1887.45,ya1-377.13},{xa2264.,ya-1129.5,x1.,x10,xa1453.,y-1131.5,y1-1132.5,ya1-226.5},{xa3054.,ya-1522.94,x1.625,x10.625,xa1611.25,y-1526.19,y1-1527.81,ya1-305.313},{xa1396.,ya-695.5,x1.,x10,xa1279.4,y-697.5,y1-698.5,ya1-139.7},{xa3288.,ya-1640.23,x1.50877,x10.508772,xa1658.004,y-1643.25,y1-1644.75,ya1-328.747},{xa3888.,ya-1939.14,x1.94372,x10.943718,xa1778.177,y-1943.03,y1-1944.97,ya1-388.617},{xa1611.,ya-802.755,x1.09785,x10.0978461,xa1322.439,y-804.951,y1-806.049,ya1-161.171},{xa1445.,ya-719.91,x1.03617,x10.0361683,xa1289.214,y-721.982,y1-723.018,ya1-144.589}}
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: 0.999242-0.000401161(1+1414xa-704.5ya)+0.399697(1+1.3595xa-0.680698ya)-0.399296(1+0.941647xa+2.02918ya)<0
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{xa-1.67183×,ya8.35913×,x1.,x12.0051×,xa1-3.34365×,y8.35913×,y18.35913×,ya11.67183×},{xa-1.67183×,ya8.35915×,x1.,x12.79706×,xa1-3.34366×,y8.35914×,y18.35914×,ya11.67183×},{xa1.67058×,ya-8.3529×,x-3.7,x13.2,xa10.3,y-2.9,y1-3.9,ya1-3.9},{xa-1.67183×,ya8.35917×,x1.,x10,xa1-3.34367×,y8.35917×,y18.35917×,ya11.67183×},{xa-1.67183×,ya8.35915×,x1.,x13.15907×,xa1-3.34366×,y8.35915×,y18.35915×,ya11.67183×},{xa-1.67185×,ya8.35925×,x1.00001,x18.82571×,xa1-3.3437×,y8.35925×,y18.35925×,ya11.67185×},{xa-1.67183×,ya8.35915×,x1.,x13.07829×,xa1-3.34366×,y8.35915×,y18.35915×,ya11.67183×},{xa-1.67184×,ya8.3592×,x1.00001,x15.87272×,xa1-3.34368×,y8.3592×,y18.3592×,ya11.67184×},{xa-1.67184×,ya8.35921×,x1.00001,x16.78524×,xa1-3.34368×,y8.35921×,y18.35921×,ya11.67184×},{xa-1.67183×,ya8.35913×,x1.,x10,xa1-3.34365×,y8.35913×,y18.35913×,ya11.67183×},{xa1.67056×,ya-8.35281×,x4.8,x1-4.3,xa12.,y-0.2,y1-3.9,ya11.1},{xa1.67055×,ya-8.35276×,x-3.9,x13.4,xa12.9,y-0.5,y13.7,ya13.5},{xa-1.67185×,ya8.35923×,x1.,x12.8371×,xa1-3.34369×,y8.35923×,y18.35923×,ya11.67185×},{xa-1.67182×,ya8.3591×,x1.,x10,xa1-3.34364×,y8.3591×,y18.3591×,ya11.67182×},{xa-1.67183×,ya8.35917×,x1.,x10,xa1-3.34367×,y8.35917×,y18.35917×,ya11.67183×},{xa-1.67184×,ya8.35921×,x1.00001,x16.21421×,xa1-3.34368×,y8.35921×,y18.35921×,ya11.67184×},{xa1.67058×,ya-8.35288×,x-4.4,x1-3.4,xa13.9,y-1.7,y12.1,ya1-4.7},{xa-1.67183×,ya8.35915×,x1.,x12.93468×,xa1-3.34366×,y8.35915×,y18.35915×,ya11.67183×},{xa-1.67183×,ya8.35915×,x1.,x12.7439×,xa1-3.34366×,y8.35915×,y18.35915×,ya11.67183×},{xa1.67057×,ya-8.35283×,x-1.8,x1-3.4,xa14.5,y-4.7,y11.3,ya1-0.4},{xa-1.67185×,ya8.35923×,x1.,x11.59339×,xa1-3.34369×,y8.35923×,y18.35923×,ya11.67185×},{xa-1.67185×,ya8.35923×,x1.,x17.53861×,xa1-3.34369×,y8.35923×,y18.35923×,ya11.67185×},{xa-1.67184×,ya8.35919×,x1.00001,x15.29528×,xa1-3.34367×,y8.35919×,y18.35919×,ya11.67184×},{xa-1.67184×,ya8.3592×,x1.00001,x15.9894×,xa1-3.34368×,y8.3592×,y18.3592×,ya11.67184×},{xa-1.67183×,ya8.35915×,x1.,x10,xa1-3.34366×,y8.35914×,y18.35914×,ya11.67183×},{xa-1.67184×,ya8.35922×,x1.00001,x17.07246×,xa1-3.34369×,y8.35922×,y18.35922×,ya11.67184×},{xa-1.67183×,ya8.35916×,x1.,x10,xa1-3.34367×,y8.35916×,y18.35916×,ya11.67183×},{xa-1.67184×,ya8.35918×,x1.,x15.05623×,xa1-3.34367×,y8.35918×,y18.35918×,ya11.67184×},{xa-1.67182×,ya8.35912×,x1.,x10,xa1-3.34365×,y8.35912×,y18.35912×,ya11.67182×},{xa1.67058×,ya-8.35288×,x1.,x14.8,xa1-2.6,y1.7,y1-1.6,ya14.4}}
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
8
10
7
10
7
10
7
10
7
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
7
10
7
10
7
10
7
10
8
10
7
10
8
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
7
10
7
10
7
10
7
10
8
10
7
10
7
10
7
10
7
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
-7
10
7
10
7
10
7
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
7
10
7
10
7
10
7
10
8
10
7
10
-6
10
7
10
7
10
7
10
7
10
8
10
7
10
7
10
7
10
7
10
7
10
8
10
7
10
-7
10
7
10
7
10
7
10
7
10
8
10
7
10
7
10
7
10
7
10
7
10
8
10
7
10
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant (rounded under precision 0.01): 1--<0
2xa
5
4ya
5
Verifying the candidate ...
Valid interpolant (simplified): 2xa+4ya>5
Elapsed time: 3.10046
Rendering graphics ...
 |
|
Done.
Benchmark C: moving to transcendental cases beyond polynomials.
Benchmark C: moving to transcendental cases beyond polynomials.
Transcendental-1:
From S. Gao et al. [TACAS’16: Interpolants in nonlinear theories over the reals].
Their result: y ≥ 0 ∧ (0.26 ≤ y ∨ (y ≤ 0.26 ∧ − 0.51 ≤ x ≤ 0.51)), ours: 152x-20y-4<0.
Transcendental-1:
From S. Gao et al. [TACAS’16: Interpolants in nonlinear theories over the reals].
Their result: y ≥ 0 ∧ (0.26 ≤ y ∨ (y ≤ 0.26 ∧ − 0.51 ≤ x ≤ 0.51)), ours:.
From S. Gao et al. [TACAS’16: Interpolants in nonlinear theories over the reals].
Their result: y ≥ 0 ∧ (0.26 ≤ y ∨ (y ≤ 0.26 ∧ − 0.51 ≤ x ≤ 0.51)), ours:
15-20y-4<0
2
x
consPhi13=y-x^2≥0;consPsi13=y+Cos[x]-0.8≤0;degree13=2;initialRange13={-5,5};
main[consPhi13,consPsi13,degree13,initialRange13]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: -0.64891+0.472941+3.40598+4.06901-7.94793<0
2
(1+0.0548189x-0.428712y)
2
(1-0.558546x-0.178727y)
2
(1+0.704484x-0.0625619y)
2
(1+0.128973x+0.104y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x2.45729,y811.},{x2.79266,y107.},{x2.83724,y10.0612},{x2489.,y6.19522×},{x-195.,y38065.},{x1245.,y1.55003×},{x1.49727,y27.3914},{x2.723,y90.},{x2.45729,y898.},{x2.56335,y6.87177},{x-3.05417,y91.},{x1593.,y2.53774×},{x2.69841,y48.},{x-1530.,y2.34092×},{x2.63629,y7.53368},{x-3.35018,y11.2237},{x-3.0436,y9.26348},{x1564.,y2.44618×},{x2.45729,y1520.},{x2.45729,y1335.},{x2.70038,y8.1875},{x-3.2926,y11.0408},{x-3.04465,y9.26991},{x-3.15605,y10.5694},{x-3.01321,y2358.},{x0.114754,y70.},{x2.54876,y90.},{x1978.,y3.91248×},{x-3.3121,y10.97},{x-3.01321,y1454.}}
6
10
6
10
6
10
6
10
6
10
6
10
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant (rounded under precision 0.1): -+-y<0
1
5
3
2
x
4
Verifying the candidate ...
Valid interpolant (simplified): 15<4+20y
2
x
Elapsed time: 12.7126
Rendering graphics ...
 |
|
Done.
Transcendental-2: no polynomial interpolant of any finite degree exists.
Transcendental-2: no polynomial interpolant of any finite degree exists.
consPhi14=Sin[x]≥0.6;consPsi14=Sin[x]≤0.4;degree14=2;initialRange14={-5,5};
main[consPhi14,consPsi14,degree14,initialRange14]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Classification failed with accuracy = 67.1218% (1278/1904).Try another degree of the polynomial kernel.
Transcendental-3:
From S. Kupferschmid and B. Becker [FORMATS’11: Craig interpolation in the presence of non-linear constraints].
Transcendental-3:
From S. Kupferschmid and B. Becker [FORMATS’11: Craig interpolation in the presence of non-linear constraints].
From S. Kupferschmid and B. Becker [FORMATS’11: Craig interpolation in the presence of non-linear constraints].
In[]:=
consPhi19=(x≥0&&x≤6)&&(y≥-2&&y≤4)&&(x<2.5y≥2Sin[x])&&(x≥2.5&&x<5y≥0.125x^2+0.41)&&(x≥5&&x≤6y≥6.04-0.5x);consPsi19=(x≥0&&x≤6)&&(y≥-2&&y≤4)&&(x<3y≤xCos[0.1Exp[x]]-0.083)&&(x≥3&&x≤6y≤-x^2+10x-22.35);degree19=7;initialRange19={-2,6};improve19=False;
In[]:=
main[consPhi19,consPsi19,degree19,initialRange19,improve19]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: -0.666901+0.124627-2.53636+8.15278-5.74116+0.000601235-0.000506225+0.0000149401-1.39675×<0
7
(1+0.0411176x-0.344019y)
7
(1+0.0066905x+0.0716982y)
7
(1+0.21896x+0.0888361y)
7
(1+0.107126x+0.214083y)
7
(1+1.67446x+1.283y)
7
(1+2.48567x+1.31599y)
7
(1+4.67958x+2.50036y)
-6
10
7
(1+5.98714x+3.58809y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x5.90766,y3.3187},{x5.95662,y3.56233},{x0.0143464,y-0.118317},{x5.7788,y3.23332},{x5.97567,y3.05217},{x4.75258,y2.58878},{x2.50006,y1.19129},{x5.7788,y3.27951},{x2.67021,y1.33611},{x5.71983,y3.19203},{x5.72004,y3.35839},{x5.90756,y3.08622},{x0.0348678,y-0.0549115},{x2.54587,y1.24035},{x5.71968,y3.32731},{x2.74237,y1.35007},{x5.7805,y3.41409},{x2.4438,y1.30762},{x5.7788,y3.38194},{x5.87411,y3.15385},{x5.90531,y3.08735},{x5.77658,y3.24103},{x5.90718,y3.08641},{x5.6725,y3.20375},{x5.95869,y3.41294},{x5.6916,y3.1942},{x0,y-0.089951},{x2.64352,y1.304},{x2.5,y1.27715},{x5.70808,y3.18596}}
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: -0.0781384+16.0355-20.1723+4.13033+0.00775594-0.00132755+0.0000212583+0.0000768941+0.0000171561-9.01455×-4.90417×<0
7
(1+0.0348678x-0.0549115y)
7
(1+0.0066905x+0.0716982y)
7
(1+0.21896x+0.0888361y)
7
(1+0.56755x+0.446724y)
7
(1+2.50006x+1.19129y)
7
(1+4.05999x+1.76081y)
7
(1+4.2561x+2.08902y)
7
(1+4.75258x+2.58878y)
-6
10
7
(1+5.97567x+3.05217y)
-7
10
7
(1+2.83051x+3.54459y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x5.99994,y3.05802},{x4.54433,y2.43578},{x5.98688,y3.05205},{x5.98852,y3.05488},{x4.3602,y2.24051},{x6.,y3.04418},{x5.97641,y3.05199},{x5.98643,y3.04944},{x4.48332,y2.38304},{x5.99533,y3.05686},{x5.99058,y3.04471},{x5.99058,y3.05118},{x4.64935,y2.52246},{x5.99994,y3.04003},{x4.67303,y2.54309},{x4.53069,y2.42975},{x5.98643,y3.05461},{x4.70552,y2.56236},{x5.97703,y3.05222},{x5.98634,y3.05175},{x5.98984,y3.04508},{x4.66361,y2.53509},{x5.98008,y3.04996},{x4.51097,y2.40813},{x5.97649,y3.05175},{x5.98413,y3.05403},{x4.58128,y2.47261},{x5.99666,y3.05166},{x5.98943,y3.05537},{x4.6775,y2.54178}}
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant: -0.0781359+16.0374-20.1727+4.12808+0.00849019-0.00135317+0.0000427064+0.0000704225+6.3198×-8.21579×-5.86576×<0
7
(1+0.0348678x-0.0549115y)
7
(1+0.0066905x+0.0716982y)
7
(1+0.21896x+0.0888361y)
7
(1+0.56755x+0.446724y)
7
(1+2.50006x+1.19129y)
7
(1+4.05999x+1.76081y)
7
(1+4.3602x+2.24051y)
-6
10
7
(1+4.53069x+2.42975y)
-6
10
7
(1+5.99994x+3.04003y)
-7
10
7
(1+2.83831x+3.49525y)
Verifying the candidate ...
Valid interpolant (simplified): -0.0781359+16.0374-20.1727+4.12808+0.00849019-0.00135317+0.0000427064+0.0000704225+6.3198×-8.21579×-5.86576×<0
7
(1+0.0348678x-0.0549115y)
7
(1+0.0066905x+0.0716982y)
7
(1+0.21896x+0.0888361y)
7
(1+0.56755x+0.446724y)
7
(1+2.50006x+1.19129y)
7
(1+4.05999x+1.76081y)
7
(1+4.3602x+2.24051y)
-6
10
7
(1+4.53069x+2.42975y)
-6
10
7
(1+5.99994x+3.04003y)
-7
10
7
(1+2.83831x+3.49525y)
Elapsed time: 61.2446
Rendering graphics ...
 |
|
Done.
Benchmark D: troubleshooting of particular cases.
Benchmark D: troubleshooting of particular cases.
Unbalanced:
Issue: the SVM training fails when encountering extremely unbalanced number of positive/negative samples, e.g., infinite samples in φ vs. merely one sample in ψ.
Solution: This is solved by specifying a weight for the positive set of samples as the number of negative samples, and a weight for the negative set of samples as the number of positive samples, when triggering the SVM. The option for specifying weights is already supported by the SVM engine we used to balance biased number of training samples.
Unbalanced:
Issue: the SVM training fails when encountering extremely unbalanced number of positive/negative samples, e.g., infinite samples in φ vs. merely one sample in ψ.
Solution: This is solved by specifying a weight for the positive set of samples as the number of negative samples, and a weight for the negative set of samples as the number of positive samples, when triggering the SVM. The option for specifying weights is already supported by the SVM engine we used to balance biased number of training samples.
Issue: the SVM training fails when encountering extremely unbalanced number of positive/negative samples, e.g., infinite samples in φ vs. merely one sample in ψ.
Solution: This is solved by specifying a weight for the positive set of samples as the number of negative samples, and a weight for the negative set of samples as the number of positive samples, when triggering the SVM. The option for specifying weights is already supported by the SVM engine we used to balance biased number of training samples.
consPhi16=x>0||x<0;consPsi16=x0;degree16=2;initialRange16={-5,5};
main[consPhi16,consPsi16,degree16,initialRange16]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant (rounded under precision 1.): -<0
2
x
Verifying the candidate ...
Valid interpolant (simplified): >0
2
x
Elapsed time: 0.110669
Done.
Benchmark E: stability w.r.t. pertabations in parameters.
Benchmark E: stability w.r.t. pertabations in parameters.
Face-ε
Face-ε
consPhi17=(-0.5≤ε1≤0.5)&&((x+4)^2+y^2-(1+ε1)^2≤0||(x-4)^2+y^2-(1+ε1)^2≤0);consPsi17=(-0.5≤ε2≤0.5)&&(x^2+y^2-64≤0&&(x+4)^2+y^2-(3+ε2)^2≥0&&(x-4)^2+y^2-(3+ε2)^2≥0);degree17=4;initialRange17={-8,8};
main[consPhi17,consPsi17,degree17,initialRange17]
Checking inputs ...
Legal inputs.
Checking unsatisfiability ...
Unsat.
Generating initial samplepoints ...
Learning a candidate interpolant at step 1 ...
Synthesized candidate interpolant: 0.999165+0.0000253122+0.000283008-0.000318974+0.0000106535<0
4
(1-7.23161x-0.678612y)
4
(1+0.165069x-0.499956y)
4
(1-4.16751x+0.343343y)
4
(1-7.36393x+2.90391y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x-7.47776,y0.930233,ε1-4.8,ε2-0.5},{x-7.50478,y1.15625,ε10.8,ε2-0.303922},{x-7.20369,y1.40938,ε1-3.5,ε20.5},{x-6.13849,y1.29493,ε1-1.8,ε2-0.5},{x-2.64636,y0.646263,ε10.5,ε2-2.3},{x-6.4895,y2.6588,ε12.7,ε20.5},{x-2.71593,y-0.775354,ε10.5,ε24.2},{x-7.09877,y1.62715,ε1-4.7,ε2-0.5},{x-3.16737,y0.065148,ε10.5,ε2-2.3},{x4.5,y-0.603391,ε10.5,ε2-3.7},{x-3.24074,y1.27397,ε10.485748,ε20.8},{x-5.28995,y2.1415,ε192.8,ε2-0.5},{x-5.28995,y2.1415,ε172.,ε2-0.5},{x3.97702,y0.881188,ε10.5,ε2-1.8},{x-6.40974,y2.56671,ε1-4.3,ε2-0.323529},{x-4.89229,y-1.06195,ε10.387051,ε2-0.2},{x-7.60652,y2.47809,ε12.8,ε20.5},{x-5.28995,y2.1415,ε1-53.2,ε2-0.5},{x-4.52223,y-0.864865,ε10.5,ε2-2.2},{x-7.49845,y-0.254902,ε12.2,ε20.5},{x5.36309,y0.626085,ε10.5,ε2-1.9},{x-7.9947,y0.291038,ε1-4.,ε20.107843},{x2.51899,y-0.237911,ε10.5,ε2-4.3},{x5.45836,y-0.173611,ε10.491157,ε2-3.7},{x-6.34787,y2.65757,ε12.2,ε2-0.5},{x3.97702,y0.881188,ε10.323171,ε21.2},{x-5.25084,y2.33791,ε1-2.8,ε2-0.47976},{x-6.28671,y1.361,ε1-1.2,ε2-0.45933},{x3.5,y1.41421,ε10.5,ε2-111.8},{x-7.50045,y0.75,ε1-1.6,ε20.0196078}}
Learning a candidate interpolant at step 2 ...
Synthesized candidate interpolant: 0.983496+0.000146816+0.00954072-0.00843967+0.000237869-0.00437809-0.0000359638+0.00261024+0.000999738-0.000681644<0
4
(1+3.51728x-2.95961y)
4
(1-1.54259x-1.27277y)
4
(1-2.71593x-0.775354y)
4
(1-7.23161x-0.678612y)
4
(1+2.51899x-0.237911y)
4
(1+3.97702x+0.881188y)
4
(1-0.349143x+1.11981y)
4
(1+0.656199x+1.12641y)
4
(1-3.24074x+1.27397y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x4.78444,y-2.53249,ε1-3.1,ε2-0.5},{x-6.5,y-0.747161,ε14.,ε2-0.390738},{x-6.5,y-0.0662377,ε10.2,ε2-0.499931},{x5.22482,y0.865926,ε10.5,ε221.8},{x-6.5,y0,ε16.3,ε2-0.5},{x3.15768,y-2.35383,ε181.7,ε2-0.5},{x-6.23539,y-1.14752,ε1-3.,ε2-0.487275},{x5.44978,y-2.20676,ε1-0.3,ε2-0.5},{x4.79063,y-2.37169,ε11.2,ε2-0.5},{x3.77893,y1.28333,ε10.477495,ε22.1},{x2.14257,y-1.81991,ε13.1,ε2-0.404573},{x3.91529,y1.49761,ε10.5,ε24.5},{x4.8416,y1.24166,ε10.5,ε2-2.8},{x6.06459,y-1.56936,ε1-4.4,ε2-0.433056},{x-6.43723,y-0.648485,ε1-2.9,ε2-0.5},{x2.34973,y-2.06912,ε11.4,ε2-0.353365},{x3.92837,y-2.68615,ε13.9,ε2-0.5},{x-6.5,y0.500923,ε1-1.2,ε2-0.450309},{x-6.48502,y-0.273277,ε12.6,ε2-0.5},{x-6.16905,y-1.26352,ε1-3.2,ε2-0.5},{x3.49793,y1.25567,ε10.352327,ε2-2.5},{x5.6861,y-1.92857,ε11.1,ε2-0.463653},{x1.7849,y-1.34055,ε1-3.8,ε2-0.483672},{x-6.27935,y-1.14409,ε1-3.3,ε2-0.46012},{x5.22482,y-2.17941,ε190.7,ε2-0.5},{x-6.5,y-0.530659,ε10.7,ε2-0.5},{x-6.5,y-0.0662377,ε11.9,ε2-0.499123},{x3.50275,y1.3123,ε10.5,ε24.5},{x4.81887,y-2.39331,ε11.2,ε2-0.5},{x-6.45881,y0.713235,ε10,ε2-0.5}}
Learning a candidate interpolant at step 3 ...
Synthesized candidate interpolant: 1.02114+0.00366138+0.0113465-0.0107977+0.000480037-0.00594953+0.000740288+0.00118133-0.000810357-2.58129×+0.00015059<0
4
(1+1.7849x-1.34055y)
4
(1-1.54259x-1.27277y)
4
(1-2.71593x-0.775354y)
4
(1-6.43723x-0.648485y)
4
(1+2.51899x-0.237911y)
4
(1-0.349143x+1.11981y)
4
(1+0.656199x+1.12641y)
4
(1-3.24074x+1.27397y)
-6
10
4
(1+3.91529x+1.49761y)
4
(1-1.42023x+2.55817y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x4.13034,y-1.49433,ε10.5,ε2-0.2},{x-2.14133,y1.69412,ε1-4.3,ε2-0.48511},{x5.31382,y-0.723786,ε10.5,ε2-98.1},{x4.69139,y-1.33116,ε10.5,ε2-2.2},{x6.56433,y0.576389,ε1-0.2,ε2-0.5},{x-4.73207,y1.28954,ε10.5,ε2-2.},{x-4.49733,y1.41516,ε10.5,ε2-0.7},{x6.55488,y0.48265,ε1-3.,ε2-0.482178},{x-2.12281,y1.69752,ε1-1.1,ε2-0.497248},{x-4.513,y1.40726,ε10.497849,ε23.3},{x4.56779,y-1.28788,ε10.5,ε2-4.4},{x6.51339,y0.409836,ε11.4,ε2-0.453414},{x4.17453,y-1.10291,ε10.5,ε20.9},{x-3.59754,y-1.44465,ε10.499667,ε2-2.7},{x-4.82519,y1.22737,ε10.5,ε2-0.8},{x-4.41447,y-1.4416,ε10.5,ε258.7},{x3.79925,y-1.48651,ε10.5,ε22.},{x-4.42191,y1.43884,ε10.499423,ε23.1},{x-4.4964,y1.40741,ε10.492385,ε2-0.9},{x-1.90457,y1.39896,ε14.,ε2-0.484843},{x3.14157,y-1.17969,ε10.466883,ε2-2.4},{x4.38202,y-1.0558,ε10.141791,ε2-4.3},{x4.61124,y-0.992706,ε10.5,ε22.8},{x3.20749,y-1.20124,ε10.450271,ε24.5},{x6.22967,y1.1372,ε1-0.8,ε2-0.5},{x5.30337,y-0.728711,ε10.5,ε2-2.9},{x-4.25472,y-1.47001,ε10.491911,ε2-4.2},{x-4.87055,y1.22153,ε10.5,ε20.3},{x-4.03529,y-1.45927,ε10.461692,ε21.8},{x-2.13002,y1.72031,ε1-2.9,ε2-0.5}}
Learning a candidate interpolant at step 4 ...
Synthesized candidate interpolant: 1.52403-0.000124787+0.00402516+0.00804423-0.00690753-0.00739461-0.00255006+0.000679629-0.00551809+0.00969903+0.0000470244<0
4
(1+3.79925x-1.48651y)
4
(1+1.7849x-1.34055y)
4
(1-1.54259x-1.27277y)
4
(1-2.71593x-0.775354y)
4
(1+2.51899x-0.237911y)
4
(1-2.64636x+0.646263y)
4
(1-6.45881x+0.713235y)
4
(1-3.24074x+1.27397y)
4
(1-1.90457x+1.39896y)
4
(1+5.63948x+2.11781y)
Verifying the candidate ...
Invalid.
Generating counter-examples...
counterExamples:{{x2.58776,y2.08446,ε10.9,ε2-0.482185},{x4.2448,y2.67778,ε13.4,ε2-0.5},{x3.43072,y2.44706,ε10.1,ε2-0.49693},{x4.83949,y2.50789,ε1-4.3,ε2-0.355329},{x4.19284,y2.49255,ε12.5,ε2-0.5},{x4.34642,y2.52518,ε1-2.4,ε2-0.5},{x3.53811,y2.59843,ε14.8,ε2-0.360841},{x2.94226,y2.3037,ε10.5,ε2-0.465072},{x5.33603,y2.11306,ε14.,ε2-0.5},{x4.34642,y2.52518,ε1-3.1,ε2-0.451169},{x4.37991,y2.77936,ε13.5,ε2-0.380665},{x4.99885,y2.44538,ε13.9,ε2-0.5},{x3.18476,y2.64231,ε1-1.2,ε2-0.496063},{x4.00577,y2.67829,ε14.9,ε2-0.335097},{x2.58776,y2.08446,ε12.8,ε2-0.483422},{x4.10277,y2.67939,ε1-3.2,ε2-0.5},{x3.88799,y2.51765,ε10,ε2-0.492424},{x4.10277,y2.67939,ε12.1,ε2-0.394973},{x4.37991,y2.77936,ε12.9,ε2-0.5},{x2.14781,y1.89371,ε13.1,ε2-0.496318},{x4.18822,y2.58271,ε1-2.3,ε2-0.410444},{x3.18476,y2.64231,ε1-3.5,ε2-0.234786},{x4.02771,y2.67954,ε13.5,ε2-0.32032},{x4.67436,y2.42683,ε1-3.,ε2-0.481217},{x2.97229,y2.42164,ε12.7,ε2-0.369307},{x4.41224,y2.54225,ε1-4.3,ε2-0.42454},{x4.41224,y2.54225,ε11.1,ε2-0.457058},{x5.13972,y2.34909,ε14.7,ε2-0.5},{x4.02771,y2.67954,ε1-4.1,ε2-0.5},{x2.97229,y2.42164,ε1-3.5,ε2-0.389392}}
Learning a candidate interpolant at step 5 ...
Synthesized candidate interpolant: 1.53827-0.000195158+0.00363926+0.00813625-0.00639824-0.00758001+0.000689778-0.00369295-0.00500866+0.00995981+0.000155111+0.000294799<0
4
(1-4.25472x-1.47001y)
4
(1+1.7849x-1.34055y)
4
(1-1.54259x-1.27277y)
4
(1-2.71593x-0.775354y)
4
(1+2.51899x-0.237911y)
4
(1-6.5x+0.500923y)
4
(1-2.64636x+0.646263y)
4
(1-3.24074x+1.27397y)
4
(1-1.90457x+1.39896y)
4
(1+2.14781x+1.89371y)
4
(1+2.58776x+2.08446y)
Verifying the candidate ...
Valid interpolant (simplified): 139.49+1.+(0.0733652+0.518624y)+14.6108+5.60134+(-42.642-0.0796609y+3.51294)+x(-1.19469-2.66849y-0.884265-2.67678)<0.639611y+0.766126
4
x
3
x
2
y
4
y
2
x
2
y
2
y
3
y
3
y
Improved valid interpolant (rounded under precision 0.001): 1+-+y+-++-++x----<0
4
x
139
y
218
3
x
268
2
2
y
19
3
y
182
4
y
25
2
x
11
36
2
y
39
1
116
y
52
2
y
157
3
y
52
Elapsed time: 12.5341
Rendering graphics ...
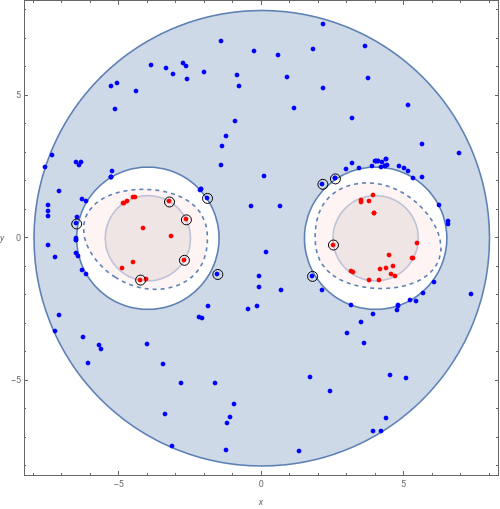 |
|
Done.
Cite this as: Mingshuai Chen, "NIL: Learning Nonlinear Interpolants" from the Notebook Archive (2021), https://notebookarchive.org/2021-08-5lcsyb7
Download
