Essays, Posts & Presentations

Quantum Gravity in (2+1) Dimensions and Multiway System

Alessandro Pisana

Author

Alessandro Pisana

Title

Quantum Gravity in (2+1) Dimensions and Multiway System

Description

This project is an attempt to reconcile the multiway paradigm and loop quantum gravity.

Quantum Gravity in
(2+1)
Dimensions and Multiway System

Alessandro Pisana

Università degli Studi di Padova

This project is an attempt to reconcile the multiway paradigm and loop quantum gravity. In particular, we focused on the deformed

(2+1)

dimensional theory by constructing gauge-invariant spin networks. Finally, we introduced the rules for an ultra-local evolution of spin networks, obtaining the deformed spin foams.

Introduction

The current paradigm describing the action of fundamental forces (strong nuclear, weak nuclear and electromagnetism) is based on the formalism of Yang-Mills theories in what is called the Standard Model of fundamental interactions. Gravity, described by General Relativity, has been excluded from this paradigm. However, there is nothing inconsistent between quantum theory and general relativity. The latter is the only consistent theory for an interacting spin-2 particle, and it is possible to treat it as an effective field theory . The problem with this view is that of not considering the formal aspects of quantum field theories. The axiomatic approach to quantum field theory provides for axioms (called Wightman axioms for the Minkowski case and Osterwalder - Schrader for the Euclidean one) it is possible to reconstruct the interacting fields from the correlation functions of free fields. All the axioms in question foresee using a Minkowski background metric, and it is not clear how to reconstruct the fields in the case of a general metric, as expected by general relativity.
Furthermore, general relativity, treated as a field theory, is non-renormalizable: it is not perturbative for energies above the Planck mass. The attempt to construct a non-perturbative quantum theory of gravity, consistent from a mathematical point of view and background-independent, takes the name of Canonical Quantum General Relativity, often abbreviated to Quantum Gravity. In its path-integral formulation, this is called Loop Quantum Gravity, where the “loops” indicate the variables introduced by Rovelli and Smolin.

Space from Combinatorics

In trying to construct an independent background theory, it is necessary to give up an a priori notion of causality. This notion is then recovered from the local relationship between the objects of which the theory is built. Objects of this type in Loop Quantum gravity are spin networks whose causal evolution constitutes spin foams. In this sense, space is a derived notion that emerges from combinatorial principles. The combinatorics then force us to give away the concept of continuous spacetime and replace it with a series of relationships between discrete objects and combine them to obtain a large scale limit, the usual physical laws.

Quantized Geometry and Loop Quantum Gravity

Loop Quantum Gravity is a theory for quantum gravity in which one tries to encode the effect of quantum superposition of geometry into a framework that is well defined conceptually and technically . The empirical inputs come from Gravity and the Quantum Theory, and the resulting theory is consistent with the Standard Model and has no ultraviolet divergences . However, it is not a theory of unification. Loop Quantum Gravity omits Supersymmetry, but there are several attempts to incorporate the gauge/gravity duality (for example, in the 3D case assuming as boundary field theory the 2D Ising model on a lattice) . Finally, there is no breaking of the Lorentz invariance at the Plank scale . In this work we focus on the

(2+1)

dimensional theory.

Spin Networks

Spin networks were first introduced by Sir. Roger Penrose in an attempt to recover continuous geometry from combinatorial laws. They are a set of vertices and edges on top of which some numbers are placed. These numbers were chosen to be units of angular momentum. In the context of Loop Quantum Gravity, the spin networks lose the connection to the original Penrose idea, and they turn out to be generalized eigenvectors of the area and volume operator. These two operators form complete commuting observables. Thus they are both diagonalized by the spin network basis.

To construct a spin network in (2+1) dimensional gravity, we consider a simple example where the foliated spacetime is such that each spatial hypersurface has a cube’s topology. The idea is to truncate the number of the degree of freedom of this hypersurface by choosing a triangulation.

In[]:=

mesh=BoundaryDiscretizeRegion@Cube[]

Out[]=

The triangulation form a graph whose links are the edges of the triangles. We extract the graph from the mesh, obtaining the Regge discretization.

In[]:=

g=MeshConnectivityGraph[mesh,0]

Out[]=

The discretized space provides us with a truncation of the Hilbert space of the quantized geometry. The idea is to take the dual graph and assign spin numbers (or colourings) to it. Then a gauge-invariant theory is obtained if the colour is allowed by triangular inequalities, which in the dual triangulation takes the form of the Clebsch-Gordon conditions for the

SU(2)

group. However, the permitted number of spin is infinite, and they can lead to divergences when, for example, “bubbles” are formed in the spin foam evolution. To overcome this problem, we work with a deformed version of SU(2), called “quantum”

SU(2)

. Here the deformation depends on a parameter q taken as the complex root of unity of degree

q = Exp[2*Pi*I/r]

It was shown that deforming the gauge group account for adding the cosmological constant to the Einstein - Hilbert action. In this quantum gravity deformed version, the maximum spin allowed is finite and depends on the deformation parameter through r, so that the cosmological constant provides an infrared cutoff of the geometry of the universe. Going back to the triangulation, we choose as a simple (and computationally lighter) parameter

r=3

constraining the domain of the spin to be

In[]:=

Domain[r_] := Table[i/2, {i, 0, r - 2}]; Domain[3]

Out[]=

0,



Then gauge conditions are imposed. In what follows, we have reported all the possible colours of the triangulation that respect the triangular inequalities. Notice that, even in the case of two allowed spins, the number of combinations is high.

Out[]=





Once the spin number is assigned, we can extract the dual graph. By taking a random coloured cube from the list, we will provide the relative spin network.

Out[]=





The dual graph is constructed, placing a node in each triangle, connecting them following triangles. The spin assignment to a segment of the triangles is then inherited by the link crossing that segment. For our example, we obtain the following spin network.

Out[]=

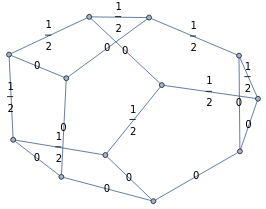
Other Examples

The procedure we implemented is general, and it is possible to change the topology or the colouring number. However, the labelling and triangulation are computationally costly: increasing the allowed colouring and the triangulation results in a prolonged evaluation time.

◼

Here we labelled the dual triangulation of a triangulated sphere, imposing the maximum spin be 1/2, reporting two random allowed colourings.

In[]:=

MeshSpinNetwork

,2

Out[]=





◼

The increasing of the colouring can be seen in the tetrahedra example. Here we raised r from 3 to 4.

In[]:=

g1=CompleteGraph[4]

Out[]=

r=3

Out[]=

r=4

Out[]=

r=5

Out[]=

Dynamical Evolution

What we succeeded to obtain are the deformed q-nets for a 3-manifold. The relative spin foams are the evolution in time of the initial spin network. If we start with a generic triangulation, we can write an ultra-local model for the Hamiltonian constrain, supposing that the Hamiltonian add new tetrahedra each time on the top of the triangulation. The new spin network formed by including the dual of this new tetrahedra then should satisfy the Clebsch-Gordon condition (to be gauge invariant). This translates into the following rules

The first rule is the one that attaches the new tetrahedra to the original q-net. So, for example, if the original network has the form

In[]:=

secondinitial = {UndirectedEdge[z, y, 1/2], UndirectedEdge[y, x, 1/2], UndirectedEdge[y, a, 1/2], UndirectedEdge[a, b, 1/2], UndirectedEdge[a, c, 1/2]}; Graph[secondinitial, EdgeLabels -> "EdgeTag", VertexLabels -> Automatic, ImageSize -> Small]

Out[]=

creates new vertices attached in the following way

Out[]=

The second rule instead changes the graph’s connectivity by replacing the two internal vertices (the two trivalent) with the other two, such that the spin current changes in the following way.

Out[]=

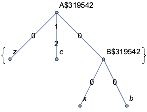
The Multiway System

As a final step, we are ready to implement the evolution into a Multiway System paradigm. By going back to the cube, we obtain the following tree graph. Each branch of this graph represents the quantum superposition of geometry. As the evolution number grows, a mini-universe example with spin-1/2 cutoff is reproduced.

In[]:=

multiwayRule = Association["StateEvolutionFunction" -> (Join[applyRule1[#1], applyRule2[#1]] & ), "StateEquivalenceFunction" -> SameQ, "StateEventFunction" -> Identity, "EventDecompositionFunction" -> Identity, "EventApplicationFunction" -> Identity, "SystemType" -> "None", "EventSelectionFunction" -> Identity]; ResourceFunction["MultiwaySystem"][multiwayRule, {initSpinNetwork}, 5, "StatesGraphStructure"]

Out[]=

As an example, we report one branch, applying only Rule 1 after 3 evolutions.

Out[]=

The final picture to have in mind is that the spacetime is built out of quantum tetrahedra; those faces are coloured that appears and disappears, changing colour in a fuzzy and furious way. As an artistic representation, here is a pictorial view of the process.

Out[]=

Transition Amplitudes

Suppose to have two graphs, one in the future and one in the past. The Hamiltonian constrain acts only on nodes, and we want to write an amplitude between the two graphs. The deformation of the

SU(2)

group leads to a class of symbols invariant under topological moves. These recoupling symbols will provide the new transition amplitude, called Turaev-Viro amplitude, for this theory. As in the previous case, suppose that the deformation parameter q is a complex root of unity with degree

. Then we define the deformed symbols in the following way.

In[]:=

Q[n_, r_] := Sin[Pi*(n/r)]/Sin[Pi/r]; FQ[n_, t_] := Product[Q[m, t], {m, 1, n}]; Δ[a_, b_, c_, t_] := FQ[-a + b + c, t]*FQ[a - b + c, t]* (FQ[a + b - c, t]/FQ[a + b + c + 1, t]); SixQSymbol[j1_, j2_, j3_, j4_, j5_, j6_, t_] := Sqrt[Δ[j1, j2, j3, t]*Δ[j1, j5, j6, t]*Δ[j4, j2, j6, t]*Δ[j4, j5, j3, t]]* Sum[(-1)^i*(FQ[i + 1, t]/(FQ[i - j1 - j2 - j3, t]*FQ[i - j1 - j5 - j6, t]* FQ[i - j4 - j2 - j6, t]*FQ[i - j4 - j5 - j3, t]*FQ[j1 + j2 + j4 + j5 - i, t]* FQ[j1 + j3 + j4 + j6 - i, t]*FQ[j2 + j3 + j5 + j6 - i, t])), {i, Max[j1 + j2 + j3, j1 + j5 + j6, j4 + j2 + j6, j4 + j5 + j3], Min[j1 + j2 + j4 + j5, j1 + j3 + j4 + j6, j2 + j3 + j5 + j6]}];

The behaviour of the deformed theory is such that in the limit where the deformation parameter goes to zero, the

SU(2)

group is recovered. For example, we compare the SixJSymbol with the deformed SixQSymbol for all the entries having

j=2

In[]:=

Plot[{SixQSymbol[2, 2, 2, 2, 2, 2, t], SixJSymbol[{2, 2, 2}, {2, 2, 2}]}, {t, 10, 100}, ScalingFunctions -> "Reverse"]

Out[]=

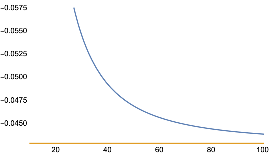
The SixQSymbol is the one that should be replaced in the partition function of the quantum gravity model. The Turaev-Viro partition function then, given two disconnected boundaries, defines a propagator which became an operator ( a projector) on the physical Hilbert space. Then if a proof model can be implemented for our multiway system, it should represent a possible transition between two spin networks and then correspond to an operator in an appropriate Hilbert space.

Code


Concluding remarks

We have successfully implemented a 3-valent spin network model for the q-deformed (2+1) quantum gravity. Future development would be constructing a causal structure for the multiway system and the extraction of the Turaev-Viro 3-manifold invariants.

Keywords

◼

Quantum Gravity

◼

Spin Network

◼

Spin Foams

◼

Quantum Groups

Acknowledgment

I am particularly grateful to my mentor, Nikolay Murzin, who provided me with all the support I needed to complete the project during school. I am also particularly thankful to him for all the code he wrote, without which ideas would not have shaped up. I am also grateful to Xerxes Arsiwalla for the exciting discussions and advice he shared on my project. Finally, I thank Stephen Wolfram and all the summer school participants for making the environment so stimulating.

References

◼

[1] Carlip, S. 1998. “Quantum gravity in 2+1 dimensions.” Cambridge University Press.

◼

[2]Rovelli, C., and Vidotto, F. 2015. “Covariant Loop Quantum Gravity: an elementary introduction to quantum gravity and spinfoam theory.” Cambridge University Press.

◼

[3]V.G. Turaev, and O.Y. Viro 1992 “State sum invariants of 3-manifolds and quantum 6j-symbols.” Topology, 31, Issue 4,Pages 865-902, ISSN 0040-9383.

Cite this as: Alessandro Pisana, "Quantum Gravity in (2+1) Dimensions and Multiway System" from the Notebook Archive (2021), https://notebookarchive.org/2021-07-6xnh97a

Quantum Gravity in (2+1)Dimensions and Multiway System

Introduction

Space from Combinatorics

Quantized Geometry and Loop Quantum Gravity

Spin Networks

Other Examples

Dynamical Evolution

The Multiway System

Transition Amplitudes

Code

Concluding remarks

Keywords

Acknowledgment

References

Quantum Gravity in
(2+1)
Dimensions and Multiway System

Code
