Regular Decagon
Author
Eric W. Weisstein
Title
Regular Decagon
Description
The regular decagon is constructible 10-sided regular polygon with Schläfli symbol {10}. The inradius r, circumradius R, and area can be computed directly from the formulas for a general regular polygon with side length s and n=10 sides, r = 1/2scot(pi/(10)) (1) = 1/2sqrt(5+2sqrt(5))s (2) R = 1/2scsc(pi/(10))=1/2(1+sqrt(5))s (3) = phis (4) A = 1/4ns^2cot(pi/(10)) (5) = 5/2sqrt(5+2sqrt(5))s^2. (6) Here, phi is the golden ratio.
Category
Educational Materials
Keywords
URL
http://www.notebookarchive.org/2019-07-0z5jpou/
DOI
https://notebookarchive.org/2019-07-0z5jpou
Date Added
2019-07-02
Date Last Modified
2019-07-02
File Size
207.67 kilobytes
Supplements
Rights
Redistribution rights reserved

Regular Decagon
Regular Decagon
Author
Author
Eric W. Weisstein
July 3, 2018
July 3, 2018
©2018 Wolfram Research, Inc. except for portions noted otherwise
Definitions
Definitions
ineq=2Sqrt[5+2Sqrt[5]]a+y≥Sqrt[2(5+Sqrt[5])]x+Sqrt[5]y&&(1+Sqrt[5])(Sqrt[5-2Sqrt[5]]x+y)≤2Sqrt[5+2Sqrt[5]]a&&Sqrt[5+2Sqrt[5]]a≥2y&&2Sqrt[5+2Sqrt[5]]a+(1+Sqrt[5])(Sqrt[5-2Sqrt[5]]x-y)≥0&&2Sqrt[5+2Sqrt[5]]a+Sqrt[2(5+Sqrt[5])]x+y≥Sqrt[5]y&&2Sqrt[5+2Sqrt[5]]a+Sqrt[2(5+Sqrt[5])]x+Sqrt[5]y≥y&&2Sqrt[5+2Sqrt[5]]a+Sqrt[10-2Sqrt[5]]x+y+Sqrt[5]y≥0&&Sqrt[5+2Sqrt[5]]a+2y≥0&&2Sqrt[5+2Sqrt[5]]a≥(1+Sqrt[5])(Sqrt[5-2Sqrt[5]]x-y)&&2Sqrt[5+2Sqrt[5]]a+Sqrt[5]y≥Sqrt[2(5+Sqrt[5])]x+y;
implreg=ImplicitRegion[ineq,{x,y}];
assum=a>0;
verts=a{{1/2(1+Sqrt[5]),0},{1/4(3+Sqrt[5]),Sqrt[5/8+Sqrt[5]/8]},{1/2,1/2Sqrt[5+2Sqrt[5]]},{-(1/2),1/2Sqrt[5+2Sqrt[5]]},{1/4(-3-Sqrt[5]),Sqrt[5/8+Sqrt[5]/8]},{1/2(-1-Sqrt[5]),0},{1/4(-3-Sqrt[5]),-(1/2)Sqrt[1/2(5+Sqrt[5])]},{-(1/2),-(1/2)Sqrt[5+2Sqrt[5]]},{1/2,-(1/2)Sqrt[5+2Sqrt[5]]},{1/4(3+Sqrt[5]),-(1/2)Sqrt[1/2(5+Sqrt[5])]}};
reg=Polygon[verts];
Figure
Figure
In[]:=
Show[LaminaData["FilledRegularDecagon","Diagram"],ImageSize300]
Out[]=

Plots
Plots
Diagram
Diagram
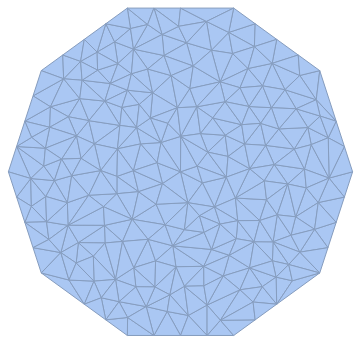
LaminaData["FilledRegularDecagon","Diagram"]

DiscretizeRegion
DiscretizeRegion
Block[{a=1},DiscretizeRegion[#]]&/@{reg,implreg}
MinValue::ztest:Unable to decide whether numeric quantities ,1,1,MaxAbs[1],Abs[1],4,Abs[5+1],Abs5+ are equal to zero. Assuming they are.
2-4+2
2(5+Times[2])(5+Times[2])
+2(5+Times[2])(5+Times[2])
-21
+41
+222(5+1)
Plus[2]
10(5+Times[2])(5+Power[2])(5+Times[2])
Plus[2]
(1++-
5
)-2+2(5+Times[2])
Plus[2]
10(5+Times[2])
Plus[2]
5+Times[2]
+5(5+Times[2])
-5+Power[2]
-5Plus[2]
1
11+1
 ,
,


Polygon
Polygon
Properties
Properties
TableForm[FullSimplify[RegularPolygonInformation[10]],TableDepth2]
sides n | 10 |
vertex angle α {rad, degrees} | 4π 5 4π 5 |
central angle β {rad, degrees} | π 5 |
inradius r | 1 2 5+2 5 |
circumradius R | 1 2 5 ) |
area A | 5 2 5+2 5 |
Equations
Equations
Properties
Properties
Rehashing named triangle objects...
Area
Area
Area
Area
Assuming[assum,FullSimplify[Area[reg/.a1]]]
5
2
5+2
5
Assuming[assum,FullSimplify[Area[implreg/.a1]]]
5
2
5+2
5
Integrate
Integrate
Assuming[a>0,Area[ineq[x,y],{x,y}]]//FullSimplify//Timing
7.5881,
5
2
5+2
5
2
a
RegionMeasure
RegionMeasure
Assuming[assum,FullSimplify[RegionMeasure[reg/.a1]]]
5
2
5+2
5
Assuming[assum,FullSimplify[RegionMeasure[implreg/.a1]]]
5
2
5+2
5
AreaInertiaTensor
AreaInertiaTensor
Assuming[a>0,AreaInertiaTensor[ineq[x,y],{x,y}]]//FullSimplify//Timing
62.2486,,0,0,
5
48
1025+458
5
4
a
5
48
1025+458
5
4
a
Centroid
Centroid
Integrate
Integrate
Assuming[a>0,Centroid[ineq[x,y],{x,y}]]//FullSimplify//Timing
{42.1837,{0,0}}
RegionCentroid
RegionCentroid
Assuming[assum,FullSimplify[RegionCentroid[reg/.a1]]]
{0,0}
Assuming[assum,FullSimplify[RegionCentroid[implreg/.a1]]]
{0,0}
Convex
Convex
TimeConstrained[Region`ConvexRegionQ[reg],600]//Timing
TimeConstrained[Region`ConvexRegionQ[implreg],600]//Timing
GeneralizedDiameter
GeneralizedDiameter
GD[n_]:=IfOddQ[n],Csc,Csca
1
2
π
2n
π
n
GD[10]
(1+
5
)aineqs=FullSimplify[And@@ineq@@@{{x1,y1},{x2,y2}},a>0]/.a1
Maximize[{(x1-x2)^2+(y1-y2)^2,ineqs},{x1,x2,y1,y2},Reals]//Timing
RadiiOfGyration
RadiiOfGyration
Assuming[a>0,FullSimplify[RadiiOfGyration[ineq[x,y],{x,y}]]]//Timing
45.8305,+a,+a
1
3
5
8
1
3
5
8
Region
Region
Block[{a=1},Through[{MinValue,MaxValue}[{x,ineq[x,y]},{x,y}]]]
$Aborted
Block[{a=1},Through[{MinValue,MaxValue}[{y,ineq[x,y]},{x,y}]]]
Quit
Lamina
Lamina
Diagonals
Diagonals
Length[v={{1/2(1+Sqrt[5]),0},{1/4(3+Sqrt[5]),Sqrt[5/8+Sqrt[5]/8]},{1/2,1/2Sqrt[5+2Sqrt[5]]},{-(1/2),1/2Sqrt[5+2Sqrt[5]]},{1/4(-3-Sqrt[5]),Sqrt[5/8+Sqrt[5]/8]},{1/2(-1-Sqrt[5]),0},{1/4(-3-Sqrt[5]),-(1/2)Sqrt[1/2(5+Sqrt[5])]},{-(1/2),-(1/2)Sqrt[5+2Sqrt[5]]},{1/2,-(1/2)Sqrt[5+2Sqrt[5]]},{1/4(3+Sqrt[5]),-(1/2)Sqrt[1/2(5+Sqrt[5])]}}]
10
ds=With[{n=Length[v]},Select[Subsets[Range[n],{2}],Mod[Subtract@@#,n]≠n-1≠1&]]
{{1,3},{1,4},{1,5},{1,6},{1,7},{1,8},{1,9},{2,4},{2,5},{2,6},{2,7},{2,8},{2,9},{2,10},{3,5},{3,6},{3,7},{3,8},{3,9},{3,10},{4,6},{4,7},{4,8},{4,9},{4,10},{5,7},{5,8},{5,9},{5,10},{6,8},{6,9},{6,10},{7,9},{7,10},{8,10}}
Length[%]
35
FullSimplify[Binomial[n,2]-n]
1
2
n(n-3)/2/.n7
14
Graphics[{{Yellow,Opacity[.2],EdgeForm[Black],Polygon[v]},Line[ds]/.Thread[Range[Length[v]]v]}]
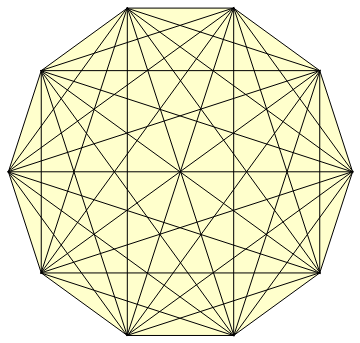
SortBy[FullSimplify[Norm[Subtract@@v[[#]]]&/@ds],N]
N::meprec:Internal precision limit $MaxExtraPrecision = 50. reached while evaluating (-3-(3+
1
4
5
)+1
4
5
).
N::meprec:Internal precision limit $MaxExtraPrecision = 50. reached while evaluating (-3-(3+
1
4
5
)+1
4
5
).
(5+,(5+,(5+,(5+,(5+,(5+,(5+,(5+,(5+,(5+,(3+(3+(3+(3+(3+(3+(3+(3+(3+(3+
1
2
5
)1
2
5
)1
2
5
)1
2
5
)1
2
5
)1
2
5
)1
2
5
)1
2
5
)1
2
5
)1
2
5
)1
2
5
),1
2
5
),1
2
5
),1
2
5
),1
2
5
),1
2
5
),1
2
5
),1
2
5
),1
2
5
),1
2
5
),5+2
,5
5+2
,5
5+2
,5
5+2
,5
5+2
,5
5+2
,5
5+2
,5
5+2
,5
5+2
,5
5+2
,1+5
5
,1+5
,1+5
,1+5
,1+5
Cite this as: Eric W. Weisstein, "Regular Decagon" from the Notebook Archive (2018), https://notebookarchive.org/2019-07-0z5jpou
Download
