Simplified Machine-Learning Workflow #1
Author
Anton Antonov
Title
Simplified Machine-Learning Workflow #1
Description
Quantile Regression (Part 1)
Category
Educational Materials
Keywords
URL
http://www.notebookarchive.org/2020-09-55roh1k/
DOI
https://notebookarchive.org/2020-09-55roh1k
Date Added
2020-09-11
Date Last Modified
2020-09-11
File Size
2.78 megabytes
Supplements
Rights
Redistribution rights reserved

Slide
1
of 18
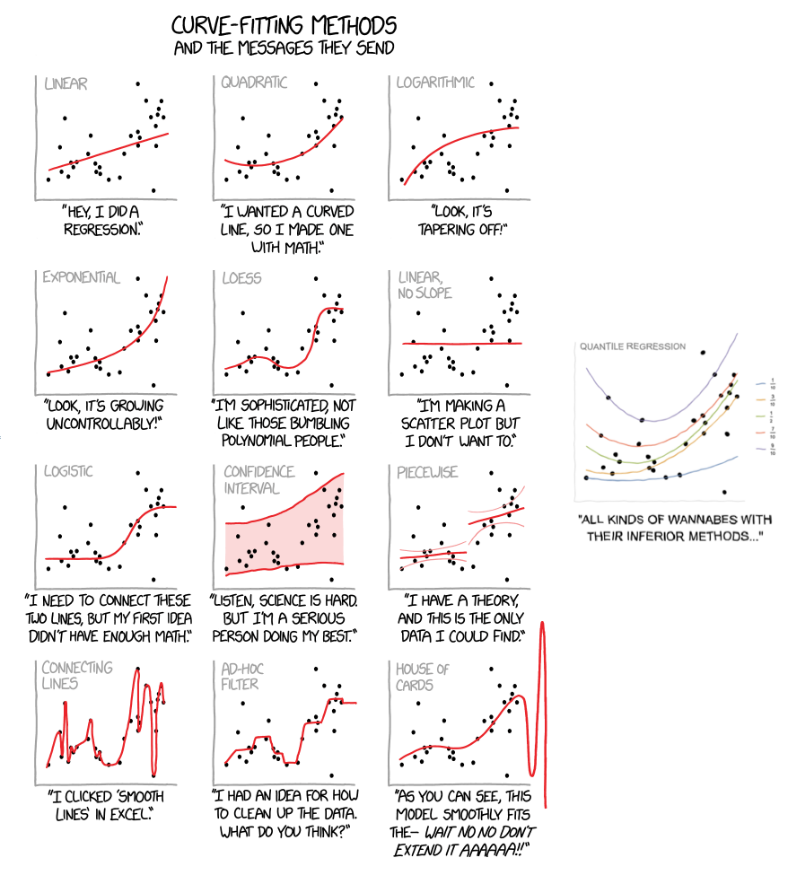
Quantile Regression monad examples
Quantile Regression monad examples
Live coding session aid
Live coding session aid
Anton Antonov
Accendo Data LLC
Accendo Data LLC
Wolfram Language live coding series
August 2019
August 2019
In[]:=
Out[]=

Slide
2
of 18
Opening
Opening
Mission statement.
Mission statement.
The goals of this workshop are to introduce the theoretical background of Quantile Regression (QR), to demonstrate QR’s practical (and superior) abilities to deal with “real life” time series data, and to teach how to rapidly create QR workflows using Mathematica or R.
Slide
3
of 18
Quantile regression workflows
Quantile regression workflows
Out[]=

Slide
4
of 18
The software monad QRMon
The software monad QRMon
When using a monad we lift certain data into the “monad space”, using monad’s operations we navigate computations in that space, and at some point we take results from it.
With the approach taken in this document the “lifting” into the QRMon monad is done with the function QRMonUnit. Results from the monad can be obtained with the functions QRMonTakeValue, QRMonContext, or with the other QRMon functions with the prefix “QRMonTake” (see below.)
Here is a corresponding diagram of a generic computation with the QRMon monad:
Out[]=

Remark: It is a good idea to compare the diagram with formulas (1) and (2).
Let us examine a concrete QRMon pipeline that corresponds to the diagram above. In the following table each pipeline operation is combined together with a short explanation and the context keys after its execution.
Out[]=
operation | explanation | context keys |
QRMonUnit[tsData]⟹ | lift data to the monad | {} |
QRMonEchoDataSummary⟹ | show the data summary | {} |
QRMonQuantileRegression[12,{0.02`,0.98`}]⟹ | do Quantile Regression with 12 knots | {data,regressionFunctions} |
QRMonLeastSquaresFit[12]⟹ | do Least Squares Fit with 12 polynomials | {data,regressionFunctions} |
QRMonPlot⟹ | plot data and regression functions | {data,regressionFunctions} |
QRMonOutliers⟹ | find outliers | {data,regressionFunctions,outliers,outlierRegressionFunctions} |
QRMonOutliersPlot | plot data and outliers | {data,regressionFunctions,outliers,outlierRegressionFunctions} |
Here is the output of the pipeline:
»
Data summary:
,
1 column 1 | ||||||||||||
|
2 column 2 | ||||||||||||
|
»
Plot:
 |
|
»
Outliers plot:

The QRMon functions are separated into four groups:
◼
operations,
◼
setters and droppers,
◼
takers,
◼
State Monad generic functions.
An overview of the those functions is given in the tables in next two sub-sections. The next section, “Monad elements”, gives details and examples for the usage of the QRMon operations.
Monad functions interaction with the pipeline value and context
Monad functions interaction with the pipeline value and context
State monad functions
State monad functions
Slide
5
of 18
QRMon single line interpreter
QRMon single line interpreter
Making a conversational agent for Quantile Regression workflows is my “end game.”
At this point I have programmed single line interpreters for variety of Machine Learning workflows.
One way to do it for Quantile Regression:
In[]:=
ToQRMonPipelineFunction["compute quantile regression using the quantiles 0.02, 0.98; show plot; display outliers plot"]
Out[]=
Function[{x,c},QRMonUnit[x,c]⟹QRMonQuantileRegression[6,{0.02,0.98},InterpolationOrder2]⟹QRMonPlot⟹QRMonOutliersPlot]
Another way to do it:
In[]:=
QRMonUnit[tsData]⟹ToQRMonPipelineFunction["show data summary"]⟹ToQRMonPipelineFunction["compute quantile regression with 10 knots and quantiles 0.02, 0.5 and 0.98"]⟹ToQRMonPipelineFunction["show plot"]⟹ToQRMonPipelineFunction["show outliers plot"];
»
Data summary:
,
1 column 1 | ||||||||||||
|
2 column 2 | ||||||||||||
|
»
Plot:
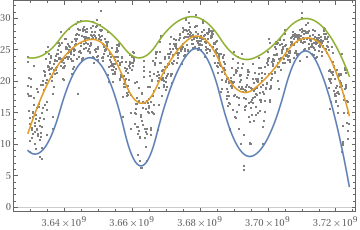 |
|
»
Outliers plot: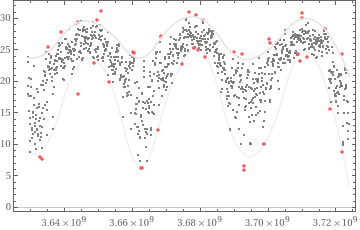

Random commands
Random commands
In[]:=
ColumnForm@Union@GrammarRandomSentences[QRMonCommandsGrammar["Normalize"True],12]
Out[]=
calculate and display dataset outliers using from 390.775 to 390.775 using 390.775 |
calculate quantile regression |
compute QuantileRegression |
display dataset together with errors together with error , data , outlier , and dataset plot with date axis |
do NetRegression using batch size 853.791 using batch size 853.791 over 853.791 hour using 853.791 rounds |
find quantile regression over 224.278 together with 348.34 , and 348.34 , 348.34 , and 348.34 and 348.34 quantiles , and using the knots 102 , with from 471.06 to 873.585 by step 520.804 quantile |
give plots with dates |
make an standard workflow using EBNFNonTerminal[<classifier-algorithm>] |
make a standard regression workflow |
net regression |
retrieve from context avmh25kl |
use dataset that has id sdan |
Slide
6
of 18
Simple pipelines
Simple pipelines
Using QR fit with the default B-splines basis.
In[]:=
QRMonUnit[distData]⟹QRMonQuantileRegression[12]⟹QRMonPlot;
»
Plot:
 |
|
In[]:=
QRMonUnit[tsData]⟹QRMonQuantileRegression[12,Range[0.1,0.9,0.2]]⟹QRMonDateListPlot[ImageSizeLarge];
»
Plot:
 |
|
Slide
7
of 18
Simple pipelines 2
Simple pipelines 2
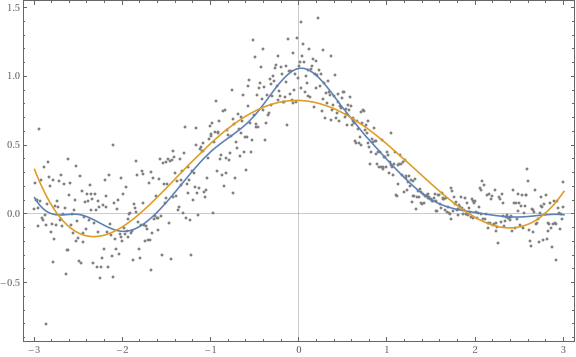
We can make pipelines that compare QR fits with Linear Regression fits.
Here with QRMonFit we use the “default” Chebyshev polynomials basis.
In[]:=
QRMonUnit[distData]⟹QRMonQuantileRegression[12,0.5]⟹QRMonFit[5]⟹QRMonPlot[ImageSizeLarge];
»
Plot:
 |
|
Here we provide our own basis for QRMonFit.
In[]:=
QRMonUnit[distData]⟹QRMonQuantileRegression[12,0.5]⟹QRMonFit[Table[,{i,0,7}]]⟹QRMonPlot[ImageSizeLarge];
i
x
»
Plot:
 |
|
Slide
8
of 18
Conditional CDF
Conditional CDF
One of the most powerful features of QR is the computation of conditional CDF’s (at specified regressor points.)
In[]:=
QRMonUnit[tsData]⟹QRMonQuantileRegression[12,Range[0.1,0.9,0.1]]⟹QRMonDateListPlot[ImageSizeLarge]⟹QRMonConditionalCDF[AbsoluteTime/@DateRange[{2016,1,1},{2017,1,1},Quantity[2,"Months"]]]⟹QRMonConditionalCDFPlot[PlotTheme"Detailed",ImageSizeMedium];
»
Plot:
 |
|
»
Conditional CDF's:3660595200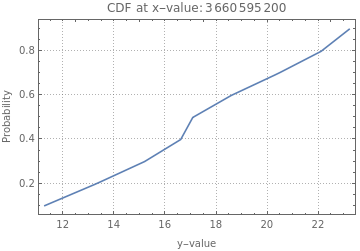 ,3665779200
,3665779200 ,3671049600
,3671049600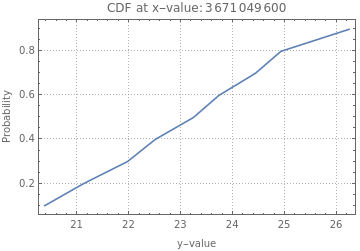 ,3676320000
,3676320000 ,3681676800
,3681676800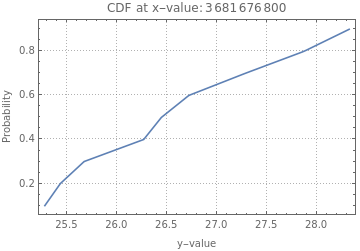 ,3686947200
,3686947200 ,3692217600
,3692217600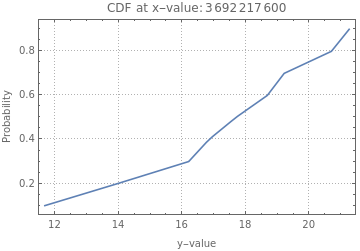







Slide
9
of 18
Outliers
Outliers
Here we find contextual outliers.
In[]:=
QRMonUnit[tsData]⟹QRMonQuantileRegression[12,{0.02,0.98}]⟹QRMonOutliersPlot[ImageSizeLarge,"DateListPlot"True];
»
Outliers plot:

What we consider outlier can be manipulated by the smallest and larges regression quantiles.
In[]:=
QRMonUnit[tsData]⟹QRMonQuantileRegression[12,{0.3,0.95}]⟹QRMonOutliersPlot[ImageSizeLarge,"DateListPlot"True];
»
Outliers plot:

Slide
10
of 18
Errors
Errors
In[]:=
QRMonUnit[distData]⟹QRMonQuantileRegression[12]⟹QRMonPlot⟹QRMonErrorPlots⟹QRMonErrorPlots["RelativeErrors"False];
»
Plot:
 |
|
»
Relative error plots:0.25 ,0.5
,0.5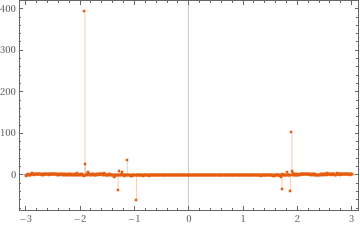 ,0.75
,0.75



»
Error plots:0.25 ,0.5
,0.5 ,0.75
,0.75



Slide
11
of 18
Over-training
Over-training
Consider over-training your QR fits. That is similar to over-training Neural Networks.
In[]:=
QRMonUnit[distData]⟹QRMonQuantileRegression[50]⟹QRMonPlot;
»
Plot:
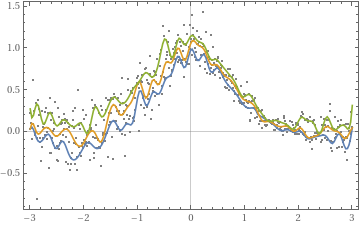 |
|
In[]:=
QRMonUnit[distData]⟹QRMonQuantileRegression[100,0.5,InterpolationOrder1]⟹QRMonPlot;
»
Plot:
 |
|
Slide
12
of 18
Getting out of the monad
Getting out of the monad
Of course at some point we would want to get out of the monad and use the objects for further computations.
In[]:=
qFuncs=QRMonUnit[distData]⟹QRMonQuantileRegression[3,InterpolationOrder2]⟹QRMonPlot⟹QRMonTakeRegressionFunctions;
»
Plot:
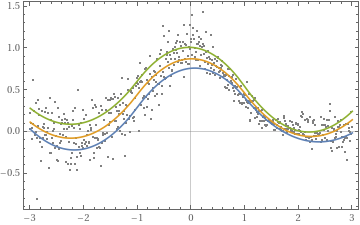 |
|
In[]:=
Simplify[#[x]]&/@qFuncs
Out[]=
0.25
,0.5
,0.75
|
|
|
In[]:=
qrObj=QRMonUnit[distData]⟹QRMonQuantileRegression[12]⟹QRMonErrors;
In[]:=
Map[ListPlot,qrObj⟹QRMonTakeValue]
Out[]=
0.25
Slide
13
of 18
Quantile Regression vs shallow Neural Networks 1
Quantile Regression vs shallow Neural Networks 1
Data
Data
In[]:=
netDistData=Rule@@@RandomSample[distData,150];
In[]:=
plot=ListPlot[List@@@netDistData,PlotStyleRed]
Out[]=
Making the model net chain
Making the model net chain
In[]:=
NeuralNetworkGraph[<|"Input"3,"Hidden 1"8,"Hidden 2"8,"Output"1|>]
Out[]=
 | |||||||||
|
Create a multilayer perceptron with a large number of hidden units:
In[]:=
net=NetChain[{150,Tanh,150,Tanh,1}]
Out[]=
NetChain
uniniti alized |
|
Train the net for 10 seconds:
In[]:=
results1=NetTrain[net,netDistData,All,TimeGoal10]
Out[]=
NetTrain Results | ||||||||||||||||
| ||||||||||||||||
Despite the noise in the data, the final loss is very low:
In[]:=
results1["FinalRoundLoss"]
Out[]=
Missing[KeyAbsent,FinalRoundLoss]
The resulting net overfits the data, learning the noise in addition to the underlying function. To see this, we plot the function learned by the net alongside the original data.
Obtain the net from the :
NetTrainResultsObject
In[]:=
overfitNet=results1["TrainedNet"]
Out[]=
NetChain
|
In[]:=
Show[Plot[overfitNet[x],{x,-3,3}],plot]
Out[]=

Slide
14
of 18
Quantile Regression vs shallow Neural Networks 2
Quantile Regression vs shallow Neural Networks 2
Quantile regression computation
Quantile regression computation
Similarities:
◼
Hidden layer nodes ↔ Knots
◼
Tanh, ReLU ↔ B-Spline, interpolation order
Slide
15
of 18
Quantile Regression vs shallow Neural Networks 3
Quantile Regression vs shallow Neural Networks 3
Interactive over-fitting
Interactive over-fitting
In[]:=
DynamicModule[{qs,qFuncs,knots,data=netDistData},Manipulate[qs={0.25,0.5,0.75};(*qFuncs=QRMonUnit[List@@@data]⟹QRMonQuantileRegression[nKnots,qs,InterpolationOrderintOrder]⟹QRMonTakeRegressionFunctions;*)qFuncs=QuantileRegression[List@@@data,nKnots,qs,InterpolationOrderintOrder];knots=Rescale[Range[0,1,1/nKnots],{0,1},{Min[data[[All,1]]],Max[data[[All,1]]]}];Show[{ListPlot[List@@@data,PlotStyleRed,GridLines{If[showKnotsQ,knots,None],None},GridLinesStyleDirective[GrayLevel[0.8],Dashed]],Plot[Through[qFuncs[x]],{x,Min[data〚All,1〛],Max[data〚All,1〛]},PerformanceGoal"Speed"]}],{{nKnots,12,"number of knots:"},0,100,1},{{intOrder,2,"interpolation order:"},1,12,1},{{showKnotsQ,False,"show knots:"},{False,True},ControlTypeCheckbox}]]
Out[]=
| |||||||||||||
| |||||||||||||
Slide
16
of 18
Anticipated questions at this point
Anticipated questions at this point
1
.How the computations are done?
2
.Why use monadic programming / pipelining?
3
.How to choose the right basis functions?
3
.1
.What if I want to basis functions other than B-Splines?
Slide
17
of 18
Using monads for conversational agents
Using monads for conversational agents
In[]:=

Slide
18
of 18
Initialization code
Initialization code
Load main packages
Load main packages
In[]:=
Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/MonadicProgramming/MonadicContextualClassification.m"];Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/MonadicProgramming/MonadicQuantileRegression.m"];Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/MonadicProgramming/MonadicNeuralNetworks.m"];Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/MonadicProgramming/MonadicTracing.m"]
»
Importing from GitHub:MathematicaForPredictionUtilities.m
»
Importing from GitHub:MosaicPlot.m
»
Importing from GitHub:CrossTabulate.m
»
Importing from GitHub:ParetoPrincipleAdherence.m
»
Importing from GitHub:StateMonadCodeGenerator.m
»
Importing from GitHub:ClassifierEnsembles.m
»
Importing from GitHub:ROCFunctions.m
»
Importing from GitHub:VariableImportanceByClassifiers.m
»
Importing from GitHub:SSparseMatrix.m
»
Importing from GitHub:OutlierIdentifiers.m
»
Importing from GitHub:QuantileRegression.m
Load data
Load data
In[]:=
Import["https://raw.githubusercontent.com/antononcube/MathematicaVsR/master/Projects/ProgressiveMachineLearning/Mathematica/GetMachineLearningDataset.m"]
In[]:=
Needs["GetMachineLearningDataset`"];dsTitanic=GetMachineLearningDataset["Titanic"];dsMushroom=GetMachineLearningDataset["Mushroom"];dsWineQuality=GetMachineLearningDataset["WineQuality"];
Distribution data
Distribution data
In[]:=
distData=Tablex,Exp[-x^2]+RandomVariateNormalDistribution0,.15
Abs[1.5-x]/1.5
,{x,-3,3,.01};QRMonUnit[distData]⟹QRMonEchoDataSummary⟹QRMonPlot;»
Data summary:
,
1 Regressor | ||||||||||||
|
2 Value | ||||||||||||
|
»
Plot:

Temperature data
Temperature data
In[]:=
tsData=WeatherData[{"Orlando","USA"},"Temperature",{{2015,1,1},{2018,1,1},"Day"}]QRMonUnit[tsData]⟹QRMonEchoDataSummary⟹QRMonDateListPlot;
Out[]=
$Aborted
»
GetData:Cannot find data.
»
QRMonBind:Failure when applying: QRMonGetData
»
QRMonBind:Failure when applying: QRMonEchoDataSummary
Financial data
Financial data
In[]:=
finData=TimeSeries[FinancialData["NYSE:GE",{{2014,1,1},{2018,1,1},"Day"}]];QRMonUnit[finData]⟹QRMonEchoDataSummary⟹QRMonDateListPlot;
::arrdepth
»
Data summary:$Failed
»
GetData:Cannot find data.
»
QRMonBind:Failure when applying: QRMonDateListPlot
Neural network construction
Neural network construction
In[]:=
ClearAll[NeuralNetworkGraph]NeuralNetworkGraph[layerCounts:{_Integer..}]:=NeuralNetworkGraph[AssociationThread[Row[{"layer ",#}]&/@Range@Length[layerCounts],layerCounts]];NeuralNetworkGraph[namedLayerCounts_Association]:=Block[{graphUnion,graph,vstyle,layerCounts=Values[namedLayerCounts],layerCountsNames=Keys[namedLayerCounts]},graphUnion[g_?GraphQ]:=g;graphUnion[g__?GraphQ]:=GraphUnion[g];graph=graphUnion@@MapThread[IndexGraph,{CompleteGraph/@Partition[layerCounts,2,1],FoldList[Plus,0,layerCounts[[;;-3]]]}];vstyle=Catenate[Thread/@Thread[TakeList[VertexList[graph],layerCounts]ColorData[97]/@Range@Length[layerCounts]]];graph=Graph[graph,GraphLayout{"MultipartiteEmbedding","VertexPartition"layerCounts},GraphStyle"BasicBlack",VertexSize0.5,VertexStylevstyle];Legended[graph,Placed[PointLegend[ColorData[97]/@Range@Length[layerCounts],layerCountsNames,LegendMarkerSize30,LegendLayout"Row"],Below]]];
Cite this as: Anton Antonov, "Simplified Machine-Learning Workflow #1" from the Notebook Archive (2020), https://notebookarchive.org/2020-09-55roh1k
Download