Towards Discretizing Metric-Affine Gravity via Elastic Hypergraphs
Author
David Chester
Title
Towards Discretizing Metric-Affine Gravity via Elastic Hypergraphs
Description
A discrete formulation (Regge calculus) of metric-affine gravity as the theory of relativistic elasticity is found to contain discrete notions of curvature, torsion, and nonmetricity, which characterize anholonomic rotations, translations, and scaling/shearing of vector transported along the hypergraph, respectively.
Category
Essays, Posts & Presentations
Keywords
metric-affine gravity, elasticity, defects, hypergraphs, lattice quivers
URL
http://www.notebookarchive.org/2021-07-60oanhf/
DOI
https://notebookarchive.org/2021-07-60oanhf
Date Added
2021-07-13
Date Last Modified
2021-07-13
File Size
3.56 megabytes
Supplements
Rights
Redistribution rights reserved

WOLFRAM SUMMER SCHOOL 2021
Towards Discretizing Metric-Affine Gravity via Elastic Hypergraphs
Towards Discretizing Metric-Affine Gravity via Elastic Hypergraphs
David Chester
Quantum Gravity Research
The most general class of non-Riemannian geometry is pursued for the Wolfram Model. A discrete formulation (Regge calculus) of metric-affine gravity as the theory of relativistic elasticity is found to contain discrete notions of curvature, torsion, and nonmetricity, which characterize anholonomic rotations, translations, and scaling/shearing of vector transported along the hypergraph, respectively. For simpler demonstration purposes, defects of cardinal lattice quivers are presumed to be recoverable from a subclass of hypergraph rewrite systems. The elastic gauge freedom of these graphs is related to the ambiguity in the implied geometry. This work is a first step towards suggesting that the Wolfram Model can support arbitrary non-Riemannian geometry. Additionally, the quantum geometry of multiway systems is speculated to connect with the higher gauge theory of bundle gerbes. If so, the Wolfram Model may one day allow for numerical relativity of discretized membrane theories such as M-theory or monstrous M-theory.
Functions
Functions
Section 1: Introduction
Section 1: Introduction
Subsection 1.1: The Wolfram model
Subsection 1.1: The Wolfram model
Wolfram' s “A New Kind of Science” proposes a computational paradigm for theoretical physics, where the Wolfram Model (WM) uses rewrite systems on hypergraphs [1]. The discrete nature of these hypergraphs leads to a notion of causal invariance that connects with quantum mechanics and relativistic physics. The Ollivier-Ricci scalar curvature was generalized to a Riemann curvature tensor, which allowed WM to make contact with Lovelock gravity and numerical relativity [2]. The causal pathways in a hypergraph allow for an abstract notion of entanglement [3]; the microscopic arrows of time may also relate to the infinite class of quantum second laws of thermodynamics [4]. Recent advances of WM also have ventured closer towards the category-theoretic formulation of quantum field theory [5], suggesting contact with higher gauge theory [6]. Progress has been made towards identifying discrete analogues of continuous gauge symmetries, but pursuing a rigorous understanding of the emergence of continuous symmetries seems fruitful. Here, a proposal to realize exact continuous gauge symmetries from discrete hypergraphs is proposed. Furthermore, a conjecture for the category-theoretic formulation of quantum parallel transport is also provided.
A graph has objects as nodes and morphisms as directed (or undirected) edges. A hypergraph may have multiple directed edges to the same node. WM can apply rewrite rules to generate graphs that lead to emergent implied geometric structure via graph distance between nodes, which in some cases leads to Riemannian manifolds. In this work, it is conjectured that discrete analogues of metric-affine gravity are found in a subset of the hypergraphs within the scope of exploration of WM. For simplicity and concreteness, the class of all graphs is studied as a subset of all hypergraphs.
In principle, notions of defects can be worked out on graphs, especially for graphs closely resembling lattices as studied in the 2021 Wolfram Winter Summer School [Patarroyo]. WM is pursuing how rewrite rules can lead to graphs with emergent properties reminiscent of interacting particles or fields in spacetime. For instance, a local patch of Z2 in the shape of a wedge has been found with the following rule:
Out[]=
{{x,y,y},{z,x,w}}{{y,t,y},{y,z,t},{w,t,t}}
By applying the same rule 301 times, the following is found, which leads to a wedge that locally is a graph resembling the Z2 lattice in the bulk:
Out[]=

To implement one notion of a hypergraph defect, consider a slight perturbation of the original rule that leads to a “defect rule”. Only a single character “w”->”x” is applied to the original rule, which can be thought of as a rewrite error similar to a mutation in DNA,
Out[]=
{{x,y,y},{z,x,w}}{{y,t,y},{y,z,t},{x,t,t}}
By applying the original rule 100 times, applying a slightly different defect rule once, and applying the original rule again 200 times, an almost identical hypergraph is found, except with a local defect. The resulting hypergraph is as follows,
Out[]=

In general, not all rules can be categorized as a defect rule, as most rules seem to destroy the structure of the original rule after applied. It is likely that the class of admissible defect rules depends on the original rule that is applied. Since it is difficult to predict what rewrite rules will lead to what emergent structure, it is similarly difficult to predict what rules are defect rules or to quickly engineer a specific defect of interest. Rather than focusing on working with arbitrary hypergraphs, the scope of this project’s exploration is restricted to graphs with labelled directed edges. These labelled edges are also restricted to always define a single abstract notion of “direction”, such that the same colored arrow cannot start from one node and end at two dissimilar nodes. Therefore, this project is restricted to the subset of hypergraphs that lead to cardinal quivers.
Recent work has suggested that defects lead to natural interpretations for elementary particles [Kleman,Millette]. If this research direction makes additional progress to find topological indices associated with the appropriate charges of the standard model spectrum, then it is conceivable that hypergraph rewrite rules similar to the defect rule above could lead to particle creation in the Wolfram Model.
Defects can be found in hypergraphs generated by a single rewrite rule that does not lead to something resembling a lattice, i.e., the most general class of hypergraphs. An irregular hypergraph would denote a high defect density such that there is a defect nearly everywhere. In this sense, a single rewrite rule may lead to a plethora of hypergraph defects, as the notion of a defect is a deviation from a regular lattice. This project is restricted to explore single defects applied to a graph resembling a lattice in order to understand how to convert the gauge theory of lattice defects into hypergraph defects. Future work may explore the most general class of hypergraphs, which must identify some scheme to characterize the closest regular graph and find all of the defects one-by-one.
Recent work has suggested that defects lead to natural interpretations for elementary particles [Kleman,Millette]. If this research direction makes additional progress to find topological indices associated with the appropriate charges of the standard model spectrum, then it is conceivable that hypergraph rewrite rules similar to the defect rule above could lead to particle creation in the Wolfram Model.
Defects can be found in hypergraphs generated by a single rewrite rule that does not lead to something resembling a lattice, i.e., the most general class of hypergraphs. An irregular hypergraph would denote a high defect density such that there is a defect nearly everywhere. In this sense, a single rewrite rule may lead to a plethora of hypergraph defects, as the notion of a defect is a deviation from a regular lattice. This project is restricted to explore single defects applied to a graph resembling a lattice in order to understand how to convert the gauge theory of lattice defects into hypergraph defects. Future work may explore the most general class of hypergraphs, which must identify some scheme to characterize the closest regular graph and find all of the defects one-by-one.
Subsection 1.2: Discrete differential geometry of metric-affine gravity
Subsection 1.2: Discrete differential geometry of metric-affine gravity
The Wolfram model focuses on structureless (non-geometric) data with hypergraphs containing nodes and hyperedges. Since condensed matter theory focuses on discrete nodes often in lattice arrangements, it is worth to recall Laughlin’s perspective on quantum gravity, who has discussed a breakdown of general relativity [7]. Similarly, Kroner investigated the differential geometry of defects in condensed matter systems [8], while Hehl et al. constructed metric-affine gravity as relativistic elasticity theory [9]. Kleinert also clarified the relationship of dislocation and disclination defects in Poincare gauge gravity [10]. Wolfram has commented in the 2021 Summer School how problems with quantum gravity and high-energy fluid dynamics are similar. In light of Wolfram’s work on fluid dynamics in cellular automata [WolframCA], the study of metric-affine gravity seems appropriate, as elastic media are hydrodynamical media with small displacements.
Curvature and torsion relate to 1-dimensional defects, while nonmetricity is for 0-dimensional defects. Since quantum gravity makes contact with gravitational excitations over very small distances, including the mathematics for the smallest forms of classical gravitation seems helpful. Dark energy, angular momentum conservation of fermions in curved spacetime [11], and the gravitational Higgs mechanism for origin of neutrino and Higgs masses [12] also motivate the search for definitions of spacetime torsion and nonmetricity from the perspective of the hypergraph. While these effects are not predicted to strongly affect dynamics, they are primarily introduced to ensure canonical energy-momentum and hyperstress tensors.
While the hypergraphs are not geometric objects, growing them to sufficiently large sizes eventually leads to implied notions of dimensionality. A single edge connecting two nodes on a graph does not have any implied distance. However, graph distance sets all edge lengths to one, which allows for geometric curvature. Note that this choice is an arbitrary local gauge choice within metric-affine gravity. Furthermore, if the edges were assigned to have different lengths, this leads to nonmetricity as a type of non-Riemannian geometry. Indeed, metric-affine gravity is a theory of gauge gravity with nonmetricity. Therefore, by allowing for all possible local ruler calibrations, this leads to the geometric structure of the hypergraph as a fictitious elastic medium. The rigid frame is one gauge choice out of many. A fluctuating medium could lead to the same physical phenomena to oscillate through different geometric perspectives.
Curvature and torsion relate to 1-dimensional defects, while nonmetricity is for 0-dimensional defects. Since quantum gravity makes contact with gravitational excitations over very small distances, including the mathematics for the smallest forms of classical gravitation seems helpful. Dark energy, angular momentum conservation of fermions in curved spacetime [11], and the gravitational Higgs mechanism for origin of neutrino and Higgs masses [12] also motivate the search for definitions of spacetime torsion and nonmetricity from the perspective of the hypergraph. While these effects are not predicted to strongly affect dynamics, they are primarily introduced to ensure canonical energy-momentum and hyperstress tensors.
While the hypergraphs are not geometric objects, growing them to sufficiently large sizes eventually leads to implied notions of dimensionality. A single edge connecting two nodes on a graph does not have any implied distance. However, graph distance sets all edge lengths to one, which allows for geometric curvature. Note that this choice is an arbitrary local gauge choice within metric-affine gravity. Furthermore, if the edges were assigned to have different lengths, this leads to nonmetricity as a type of non-Riemannian geometry. Indeed, metric-affine gravity is a theory of gauge gravity with nonmetricity. Therefore, by allowing for all possible local ruler calibrations, this leads to the geometric structure of the hypergraph as a fictitious elastic medium. The rigid frame is one gauge choice out of many. A fluctuating medium could lead to the same physical phenomena to oscillate through different geometric perspectives.
Making contact to Riemannian curvature is equivalent to the coincident gauge in symmetric teleparallelism, which naturally leads to the Eddington energy-momentum pseudotensor as a canonical energy-momentum tensor [13]. This theory also contains the topological Gauss-Bonnet term, which recently has allowed for finite perturbative two-loop graviton scattering [14]. One may speculate that counterterms for higher loops may be provided by higher-dimensional operators in Lovelock gravity, whose coefficients have recently been predicted in string theory [Wang2021].
In addition to being represented as a nonlinear sigma model [15], general relativity can also be described in three subsectors of metric-affine gravity, dubbed the trinity of gravity [16]. General relativity contains only Riemannian curvature, while metric teleparallel equivalent to GR contains only torsion, and symmetric teleparallel equivalent to GR includes only nonmetricity [17, 13]. The lack of geometric structure in the hypergraph provides a true continuous gauge symmetry, as one has the freedom to interpret any edge as having any length, which is a local and continuous symmetry. While all torsion and curvature may be expressed as nonmetricity, not all nonmetricity may be expressed as torsion or as curvature. Therefore, the full non-Riemannian geometry should describe a larger span of the space of hypergraphs.
Since no formulation of Yang-Mills theory leads to finite self-energy, yet recent progress has been made with torsional regularization in QED [Poplawski], one may hope that gravity as a QFT may be understood once the double copy of non-perturbative Yang-Mills theory, potentially with aid from higher-dimensional operators for UV completion [DoubleCopy,14]. It is conceivable that torsion could also help with Yang-Mills theory, and gravity as nonmetricity has already been shown to lead to canonical stress-energy-momentum. Recently, a non-Abelian Navier-Stokes fluid was introduced and shown to have solutions related to a tensor fluid [18]. Since elastic media are fluids with small displacements, this provides further support for the relationship of relativistic elasticity and gravitational theory, as hydrodynamical solutions of different theories have the same relationship as Yang-Mills theory and gravity. Scattering arbitrary fluid elements at high energies is difficult, no matter if this fluid has Abelian charge, non-Abelian charge, or tensorial charge.
While hypergraphs are the most abstract, latching onto lattice quivers is more abstract than a specific geometry. As early as 2002, super Yang-Mills theory has been placed within a quiver mechanics formulation [Denef]. If the supersymmetry is removed, this roughly leads to bosonic force carriers as nodes and fermionic matter fields as arrows [Denef]. The utilization of a matrix model compactifies everything to a point, which is similar to approaches to M-theory [Schreiber]. While the Lagrangian below has simpler quantum-mechanical behavior than the standard model, the classical theory is sophisticated enough to contain fields close to the standard model spectrum. Most likely, a hypergraph model could be made to closely resemble the quiver mechanics below:
In addition to being represented as a nonlinear sigma model [15], general relativity can also be described in three subsectors of metric-affine gravity, dubbed the trinity of gravity [16]. General relativity contains only Riemannian curvature, while metric teleparallel equivalent to GR contains only torsion, and symmetric teleparallel equivalent to GR includes only nonmetricity [17, 13]. The lack of geometric structure in the hypergraph provides a true continuous gauge symmetry, as one has the freedom to interpret any edge as having any length, which is a local and continuous symmetry. While all torsion and curvature may be expressed as nonmetricity, not all nonmetricity may be expressed as torsion or as curvature. Therefore, the full non-Riemannian geometry should describe a larger span of the space of hypergraphs.
Since no formulation of Yang-Mills theory leads to finite self-energy, yet recent progress has been made with torsional regularization in QED [Poplawski], one may hope that gravity as a QFT may be understood once the double copy of non-perturbative Yang-Mills theory, potentially with aid from higher-dimensional operators for UV completion [DoubleCopy,14]. It is conceivable that torsion could also help with Yang-Mills theory, and gravity as nonmetricity has already been shown to lead to canonical stress-energy-momentum. Recently, a non-Abelian Navier-Stokes fluid was introduced and shown to have solutions related to a tensor fluid [18]. Since elastic media are fluids with small displacements, this provides further support for the relationship of relativistic elasticity and gravitational theory, as hydrodynamical solutions of different theories have the same relationship as Yang-Mills theory and gravity. Scattering arbitrary fluid elements at high energies is difficult, no matter if this fluid has Abelian charge, non-Abelian charge, or tensorial charge.
While hypergraphs are the most abstract, latching onto lattice quivers is more abstract than a specific geometry. As early as 2002, super Yang-Mills theory has been placed within a quiver mechanics formulation [Denef]. If the supersymmetry is removed, this roughly leads to bosonic force carriers as nodes and fermionic matter fields as arrows [Denef]. The utilization of a matrix model compactifies everything to a point, which is similar to approaches to M-theory [Schreiber]. While the Lagrangian below has simpler quantum-mechanical behavior than the standard model, the classical theory is sophisticated enough to contain fields close to the standard model spectrum. Most likely, a hypergraph model could be made to closely resemble the quiver mechanics below:

(Commentary on content from the Appendix in Ref. [Denef].)
Recently, fundamental particles such as photons, massive bosons, quarks, and leptons have been placed in the context of crystal defects [Millette]. For Millette, dislocations and disclinations were associated with bosons and fermions, respectively. While this appears to be different than Denef, it seems that Denef is referring to the local interactions, while Millette is focusing on the conception of spacetime.
In principle, the interactions of the theory expressed as quivers could naturally lead to the emergence of a spacetime lattice, similar to Truini et al.’s “Borcherdization” of E8 (first coined by Lisi at the 2018 Advances in Quantum Gravity conference) [Truini]. While a finite-dimensional root polytope associated with a finite-dimensional Lie algebra may define the interactions, the infinite-dimensional lattice and further extensions (Kac-Moody/Virasoro/Borchards) are thought to lead to second quantization for a nonperturbative formulation quantum gravity on a discrete lattice. Irwin has also led Quantum Gravity Research to explore infinite-dimensional quasicrystalline Lie algebras.
This work argues that a subset of hypergraphs naturally lead to lattice quivers whose defects may represent fundamental particles. Section 2 implements Mathematica functions to add zero-dimensional defects to Graphs and QuiverGraphs that can construct higher-dimensional defects associated to the fundamental particle assignments of Millette. Section 3 explores examples of anholonomic properties of worldcrystal defects for theories of gravitation.
In principle, the interactions of the theory expressed as quivers could naturally lead to the emergence of a spacetime lattice, similar to Truini et al.’s “Borcherdization” of E8 (first coined by Lisi at the 2018 Advances in Quantum Gravity conference) [Truini]. While a finite-dimensional root polytope associated with a finite-dimensional Lie algebra may define the interactions, the infinite-dimensional lattice and further extensions (Kac-Moody/Virasoro/Borchards) are thought to lead to second quantization for a nonperturbative formulation quantum gravity on a discrete lattice. Irwin has also led Quantum Gravity Research to explore infinite-dimensional quasicrystalline Lie algebras.
This work argues that a subset of hypergraphs naturally lead to lattice quivers whose defects may represent fundamental particles. Section 2 implements Mathematica functions to add zero-dimensional defects to Graphs and QuiverGraphs that can construct higher-dimensional defects associated to the fundamental particle assignments of Millette. Section 3 explores examples of anholonomic properties of worldcrystal defects for theories of gravitation.
Subsection 1.3: Higher gauge theory of discrete bundle gerbes
Subsection 1.3: Higher gauge theory of discrete bundle gerbes
After demonstrating the parallel transport of vectors along the most general non-Riemannian hypergraph, the parallel transport of multiple vectors is of interest, which is necessary for probing the most general notion of nonmetricity. This allows for even more subtle forms of gravitation, which ultimately motivate the modelling of discrete brane bits as a polytope or collection of vectors. Once the parallel transport of a finite number of variables on a single path is understood, the next step is to study the parallel transport of multiple vectors along multiple paths. This makes contact with bundle gerbes associated with parallel transport of membranes in higher gauge theories.
The question still remains, can the Wolfram Model connect to string theory? Perturbative string field theory makes contact with topological quantum field theory, while nonperturbative string and membrane theories are described by large-N limits of matrix models [Maldacena]. Supergravity found membranes that generalize strings, which led to M-theory [Duff,Witten]. Currently, the full details of M-theory is not well understood, partially due to a lack of mathematical understanding of non-Abelian bundle gerbes. While significant progress with gerbes has been difficult, focusing on discrete bundle gerbes may help provide some simplification. The parallel transport of quantum gravity includes the parallel transport of nonlinear tensor fields simultaneously along multiple paths.
If the Wolfram Model could abstract quiver mechanics to hypergraphs and make progress with higher gauge theories of non-Abelian bundle gerbes, then numerical relativity of bundle gerbes would demonstrate that WM has a solid connection to not only string theory, but also M-theory, F-theory, and beyond. Section 4 provides a description on how to relate higher defects of metric-affine gravity to higher gauge theory of membrane transport. Unfortunately, time constraints did not permit progress on implementing discrete bundle gerbes in Mathematica.
The question still remains, can the Wolfram Model connect to string theory? Perturbative string field theory makes contact with topological quantum field theory, while nonperturbative string and membrane theories are described by large-N limits of matrix models [Maldacena]. Supergravity found membranes that generalize strings, which led to M-theory [Duff,Witten]. Currently, the full details of M-theory is not well understood, partially due to a lack of mathematical understanding of non-Abelian bundle gerbes. While significant progress with gerbes has been difficult, focusing on discrete bundle gerbes may help provide some simplification. The parallel transport of quantum gravity includes the parallel transport of nonlinear tensor fields simultaneously along multiple paths.
If the Wolfram Model could abstract quiver mechanics to hypergraphs and make progress with higher gauge theories of non-Abelian bundle gerbes, then numerical relativity of bundle gerbes would demonstrate that WM has a solid connection to not only string theory, but also M-theory, F-theory, and beyond. Section 4 provides a description on how to relate higher defects of metric-affine gravity to higher gauge theory of membrane transport. Unfortunately, time constraints did not permit progress on implementing discrete bundle gerbes in Mathematica.
Section 2: Classification of worldcrystal defects
Section 2: Classification of worldcrystal defects
As a proposal to implement defects, start with a rule that leads to the Z2 and Z3 lattices. To construct a defect, attempt to apply one different rule at a different time and find a way to go back to the old rule such that a local defect is found. Due to time constraints, defects from crystals are classified on graphs. The definition of higher-dimensional defects on graphs are constructed directly from zero-dimensional defects such that they can be found for inherently non-geometric graphs and quiver lattices.
A defect is constructed by cutting a (hyper)graph, add or remove nodes and edges, and apply some surgery to stitch the (hyper)graph back together. The cardinals on quiver lattices are helpful for quickly implementing these defects, as the number of defects possible is highly restricted. The space of hypergraphs allows for each defect to have other possibilities about how to stitch together the graph after applying a cut. A simple demonstration of gravitational gauge transformations can lead to the gravitation to be turned from nonmetricity into torsion or visa-versa. The diffeomorphism invariance allows for arbitrary metric-affine schemes, which includes the slipping and rolling of a tangent manifold on the base manifold for notions of Born’s reciprocity, relative locality, or what Kroner may call a strain/stress phase space [Kroner].
A defect is constructed by cutting a (hyper)graph, add or remove nodes and edges, and apply some surgery to stitch the (hyper)graph back together. The cardinals on quiver lattices are helpful for quickly implementing these defects, as the number of defects possible is highly restricted. The space of hypergraphs allows for each defect to have other possibilities about how to stitch together the graph after applying a cut. A simple demonstration of gravitational gauge transformations can lead to the gravitation to be turned from nonmetricity into torsion or visa-versa. The diffeomorphism invariance allows for arbitrary metric-affine schemes, which includes the slipping and rolling of a tangent manifold on the base manifold for notions of Born’s reciprocity, relative locality, or what Kroner may call a strain/stress phase space [Kroner].
In[]:=

Functions in Mathematica were developed to generate all Graph and LatticeQuiver defects in terms of sums over zero-dimensional defects, which is the discrete analogue of the integrals shown above. Due to the 3-week time scale, a balance between exhaustively discussing all defects, showing explicit examples in Mathematica, and writing code that was implemented properly had to be made. Each defect was discussed in words. Code for all defects in 2-dimensions, including the 0-dimensional defects and 1-dimensional defects, was written in a manner that had flexible options for working with Graphs in Mathematica and QuiverGraphs from Taliesin Beynon’s GitHub repository were used for this project [Beynon].
Subsection 2.1: 0-dimensional defects
Subsection 2.1: 0-dimensional defects
The vacancy and interstitial defects are 0-dimensional defects that remove or add a vertex point. Since lattice quivers allow for an abstract notion of regular tilings, defects of lattice quivers can be studied without specifying the geometry precisely. Nonmetricity can correspond to 0-dimensional defects, however, this concept has not been investigated for gravity [Kroner]. 0-dimensional defects are implemented so the analysis of parallel transport around such defects can be studied in a gravitational context.
Subsubsection 2.1.1: Vacancy defects
Subsubsection 2.1.1: Vacancy defects
Consider a 5x5 patch of a square lattice quiver, which contains two cardinals that are an abstraction of translations in the x and y directions of a 2-dimensional space. While UndirectedEdges are utilized, the graphs are presumed to have directed edges such that upper-case cardinal edges are the opposite direction of lower-case cardinal edges:
Out[]=
 |
|
Out[]=
 |
|
A vacancy defect is a 0-dimensional defect that removes a single point. To apply a vacancy defect on lattice quivers, the only information needed is to specify a single vertex label. For a hypergraph without cardinals, the plethora of options on how to reconnect the adjacent nodes of the vacancy leads to additional freedom. Since the hypergraphs were argued to lead to Riemannian geometry, it seems likely that hypergraphs could also lead to quiver diagrams, as these contain less structure.
To develop a formalism for constructing arbitrary defects, each defect can be thought of as a function that takes a graph and details that specify the defect. A vacancy defect is applied to the central vertex labelled 1 below:
Out[]=
 |
|
VacancyDefect allows for additional options to reconnect vertices after the defect is applied. A third value to the function may be provided to add additional edge connections after the defect is applied. The third value defaults to {} to lead to no new connections. Additionally, if None is provided, the maximal number of edges that lead to admissible cardinals across the vacancy defect are found:
Out[]=
 |
|
VacancyDefect also can work with graphs and specify the precise edge connections. This also works with adding new cardinal quivers, as shown below:
In[]:=
vacancy3=VacancyDefect[square,1,DirectedEdge@@#&/@{{2,5,"a"},{5,4,"b"},{4,3,"a"},{3,2,"b"}}];vacancy3=AnnotationDelete[vacancy3,Cardinals]
Out[]=
 |
|
Subsubsection 2.1.2: Interstitial defects
Subsubsection 2.1.2: Interstitial defects
An interstitial (or excess) defect adds a single node to a graph, rather than removing a node. Specifics for how edges are connected to this new node must be specified. The name of the node can be given optionally, but if it is left out, the code automatically generates a new vertex label as the minimal positive integer that is greater than all integer vertex labels. In order to allow for an autogenerated vertex label, the edge connection can use a blank “” as a representation for the new vertex label. (Hopefully, no cardinals are named “”, as this may cause issues.)
If a QuiverGraph is entered, the function allows for three different ways to preserve cardinal uniqueness if the new edges cause conflicts. The fourth input cardinalSelect defaults to “NewCardinals”, which changes any new edges to new cardinals.
If a QuiverGraph is entered, the function allows for three different ways to preserve cardinal uniqueness if the new edges cause conflicts. The fourth input cardinalSelect defaults to “NewCardinals”, which changes any new edges to new cardinals.
Out[]=
 |
|
Setting cardinalSelect = “OldEdges” does not add any new cardinals and keeps the old edges that were in conflict, deleting all new conflicting edges.
Out[]=
 |
|
Setting cardinalSelect = “NewEdges” does not add any new cardinals, keeps all the new edges, and deletes any old conflicting edges.
Out[]=
 |
|
Finally, if a QuiverGraph is entered and one does mind violations of cardinal uniqueness, cardinalSelect = “Graph” can be chosen, which ensures that all of the old and new edges are kept in the final graph.
Out[]=
 |
|
The default for InterstitialDefect is to set cardinalSelect = “” such that an inverse can always be identified by adding a Vacancy defect,
Out[]=
 |
|
Vacancy defects that do not add new cardinal edges can also be thought of as an inverse of a particular interstitial defect, provided that the appropriate cardinal edges are specified,
Out[]=
 |
|
Subsubsection 2.1.3: Vacancy/interstitial dipole defects
Subsubsection 2.1.3: Vacancy/interstitial dipole defects
If a vacancy and interstitial defect are applied to a graph with different nodes, this can be thought of as a zero-dimensional dipole defect that results in translating a node from one location on a graph to another, which models a notion of hopping.
Out[]=

Summing over these types of defects should be useful for generating screw dislocations from 0-dimensional defects. Next, the 1-dimensional dislocations are introduced.
Subsection 2.2: 1-dimensional dislocation defects
Subsection 2.2: 1-dimensional dislocation defects
The 1-dimensional defects are classified as either dislocations or disclinations. Dislocations are a line integral of 0-dimensional defects. Disclinations are an angular integral of dislocations. In 2-dimensions, the dislocations and disclinations are uniquely edge dislocations and wedge disclinations. In 3-dimensions, the screw dislocation, splay disclination, and twist disclination all become possibilities [10]. It is conceivable that more exotic 1-dimensional defects could be found in higher dimensions, but these will be neglected.
A 2-dimensional edge dislocation and 3-dimensional screw dislocation are shown below. Completing the screw dislocation leads to a parking garage-like structure.
In[]:=

Out[]=
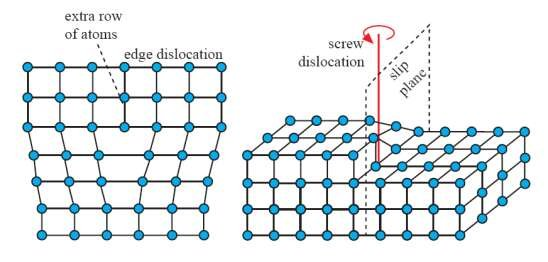
Subsubsection 2.2.1: Edge dislocation
Subsubsection 2.2.1: Edge dislocation
An edge can be specified in a Graph via Line or in a QuiverGraph via HalfLine:
Out[]=
 |
|
The edge dislocation is simplest in 2-dimensions, which removes a half-line from a QuiverGraph. This can also be specified by a list of two vectors, such that the shortest path connecting the two points is used. Additionally, a HalfLine[] may be specified, all of which can lead to:
Out[]=
 |
|
Since hexagonal lattices have two vertex types, reconnecting dislocation lines automatically as shown above needs improvement, but the vertices are removed properly:
Out[]=
 |
|
Additionally, a list of vertices may be added, which removes all of them, assuming a graph. This may not guarantee to return a valid QuiverGraph. A third variable vacancyStitch can be added to decide how the succession of vacancy defects should be applied. In general, vacancyStitch = {} leads to a QuiverGraph, but this results in tearing the graph without any new cardinal edges added. Alternatively, vacancyStitch = None is the default, which allows for hopping as shown in the first graph below:
In[]:=
dislocation2=EdgeDislocation[square,{1,4,9,20,25}]dislocation3=EdgeDislocation[square,{1,4,9,20,25},{}]EdgeDislocation[hex,{1,8},{DirectedEdge[4,7,"a"],{},{}}]
In general, an edge dislocation adds or removes a line. Unfortunately, general code was not written to add an edge dislocation line, but an example is shown below:
Out[]=
 |
|
In 3 dimensions, a line dislocation removes a plane. Here is the quiver lattice for a cube:
Out[]=
|
A graphical representation of a line dislocation applied to the cubic lattice quiver is shown below:
Out[]=
|
Subsubsection 2.2.2: Screw dislocation
Subsubsection 2.2.2: Screw dislocation
3-dimensional crystals have edge dislocations as an insertion or deletion of a plane, such that a d-dimensional edge dislocation has co-dimension 1 modifications. The screw dislocation can be formed by a sum or integral of vacancy/interstitial dipole defects parallel to the defect line while rotating about the defect line.
In[]:=

Since full support for 3D quiver lattices is currently under development, the picture below gives a rough sketch of how a screw dislocation could work on a discrete graph such as the 3D cubic quiver lattice. The black edges are all edges in planes of z = const., while orange edges show some of the edges in the z-direction. The blue edges denote all of the edges modified from a succession of vacancy/interstitial dipoles, which led to the destruction of some black edges:

Subsubsection 2.2.3: Nonmetricity vs torsion
Subsubsection 2.2.3: Nonmetricity vs torsion
Graphs have the freedom to interpret some defects as nonmetricity or torsion, as the graph does not contain geometric structure. Depending on the gravitational theory of interest, one convention versus another may be preferred. For instance, the diagram below depicts how parallel transporting about the same interstitial defect can lead to torsion or nonmetricity, depending on if the graph distance convention is utilized before or after the defect is inserted.
In[]:=
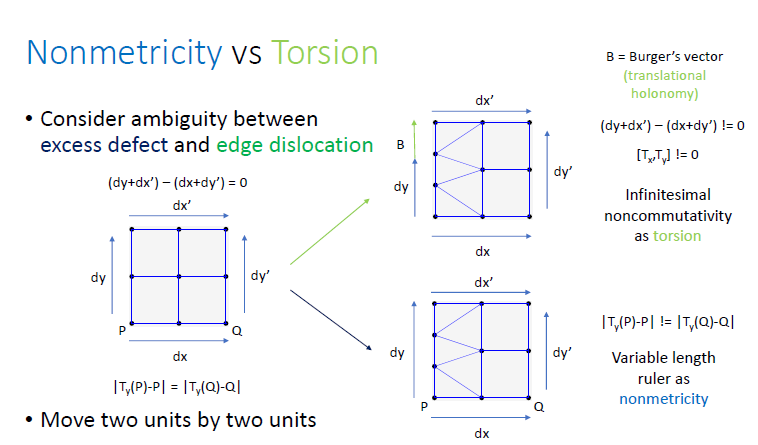
(Image courtesy of Quantum Gravity Research - Private Meeting 2020.)
The top right depicts the scenario if graph distance is used after an interstitial/excess defect is added. The emergent geometry finds noncommutativity, as dx+dy’ leads to a different point than dy+dx’, which leads to an excess in graph distance of one step, characterized by the Burger’s vector. The bottom right scenario utilizes the graph distance from before the defect. Instead, the length of a step in the y-direction is modified to 2/3 along dy, such that dx+dy’=dx’+dy and commutativity is preserved, yet the length of a ruler changes as a function of position (a characteristic of nonmetricity).
Subsection 2.3: 1-dimensional disclination defects
Subsection 2.3: 1-dimensional disclination defects
Next, the disclination defects are briefly reviewed. In 2D, only wedge disclinations are possible. For 3D, wedge, splay, and twist disclinations can be found. Higher dimensions may lead to more exotic disclinations, but it is not clear if these have been classified.
In[]:=

(Image courtesy of Millette 2018 [Millette].)
Subsubsection 2.3.1: Wedge disclination
Subsubsection 2.3.1: Wedge disclination
A wedge disclination is shown on a 2D square QuiverLattice. Since the vertex positions are irrelevant, the rendered Graph is also shown:
Out[]=
 |
|

A wedge disclination can also be formed by adding an angular wedge to an applied cut.
Subsubsection 2.3.2: Splay disclination
Subsubsection 2.3.2: Splay disclination
A splay disclination is similar to a wedge disclination in 3D, except the angle in the third dimension perpendicular to the wedge is taken as a (linear) function of the height along the third dimension. Higher-dimensional examples may also lead to more exotic types of splay disclinations with multiple angles varied rather than one.
Subsubsection 2.3.3: Twist disclination
Subsubsection 2.3.3: Twist disclination
A twist disclination, as the name implies, adds a twist in addition to the wedge disclination. The twist is applied by rotating in a plane that has one axis aligned with the wedge dislocation line and the other perpendicular to the angular direction of the wedge.
Subsubsection 2.3.4: Torsion vs curvature
Subsubsection 2.3.4: Torsion vs curvature
Similar to the ambiguity of nonmetricity and torsion found with a collection of zero-dimensional defects, the same ambiguity is found for torsion and curvature for a collection of one-dimensional defects. An angular sum of edge dislocations is equivalent to a disclination, just as two oppositely charged disclinations superimposed can lead to an edge dislocation. Similarly, a graph with 1-dimensional defects may lead to different geometries that interchange torsion and curvature. General relativity and metric-teleparallel-equivalent general relativity both result in Einstein’s field equation dynamics. The former has curvature while the latter has torsion; both are subsectors of metric-affine gravity.
Coordinate invariance in metric-affine gravity is a gauge symmetry, yet metric-affine gravity still always has implied geometry. However, it is clear that different subsectors of MAG can lead to the same physics. The most general notion of coordinate independence therefore can be generalized to the geometry independence of causal hypergraphs. One may choose the geometric scheme for the causal relationships of events from initial to final conditions.
In[]:=

As shown above, all defects can be defined from combinations of the zero-dimensional defects. While the author independently realized this, according to Hehl, Kroner showed that these correspond to nonmetricity [Kroner].
Subsection 2.4: 2-dimensional defects
Subsection 2.4: 2-dimensional defects
Domain walls can appear via two-dimensional defects, which lead to the possibility of polytopes to be formed via isolation of multiple nearly-coincident domain walls. Domain walls are topological solitons due to a spontaneously broken discrete symmetry, which have been studied in the context of thick branes [Dzhunushaliev]. A future goal is to work towards a notion of a discretized D3-brane in 3+1 dimensions as a convex polytope abstracted to a graph or quiver lattice. To implement domain walls in a simple way, additional cardinals could be introduced for inside and outside the brane.
Section 3: Holonomic parallel transport and autoparallels in discrete metric-affine gravity
Section 3: Holonomic parallel transport and autoparallels in discrete metric-affine gravity
In general relativity, the metric tensor is uniquely specified by the collection of all possible infinitesimal loops in the space of possible paths. The parallel transport of a vector around a loop probes the curvature by measuring how much the tangent vector rotates after completing a loop. The Levi-Civita connection naturally arises from the path length of a curve
μ
Γ
αβ
S =dτ, δS =0,
b
∫
a
g
μν
μ
x
ν
x
μ
¨
x
μ
+Γ
αβ
α
x
β
x
In metric-affine gravity, transporting along the autoparallel differs from the parallel transport in that the torsion and nonmetricity may lead to a translation or rescaling of the tangent vector transported around a loop [Damianos]. The parallel transport and autoparallels are equivalent in general relativity, as the parallel transport only is in terms of the Levi-Civita connection, while metric-affine gravity has a general affine connection with an independent metric . The affine connection most generally includes the Levi-Civita connection, the contortion , and the disformation ,
μ
A
αβ
g
μν
μ
K
αβ
μ
L
αβ
μ
A
αβ
μ
Γ
αβ
μ
K
αβ
μ
+L
αβ
The autoparallel transport equation is given by,
μ
¨
x
μ
+A
αβ
α
x
β
x
The Ambrose-Singer theorem finds the curvature form from the holonomy of a connection in a principle bundle [AmbroseSinger]. For this reason, it helps to review differential forms in metric-affine gravity.
An n-dimensional differentiable manifold has a tangent space. The local frame is introduced as a vector basis for the tangent space, where Latin indices are used for flat anholonomic frame indices, while Greek indices are used for curved holonomic coordinate indices. The frame is expanded as
e
a
μ
e
a
∂
μ
e
a
b
θ
μ
e
a
b
e
μ
b
δ
a
b
θ
b
e
b
e
μ
μ
dx
which leads to the metric tensor in terms of the frame field (also called the vierbein or tetrad in D=3+1),
g
μν
a
e
μ
b
e
ν
g
ab
where the most general metric-affine geometry can have != . An arbitrary vector has an exterior covariant derivative D with spin connection 1-form ,
g
ab
η
ab
a
x
a
ω
b
D = d + .
a
x
a
x
a
ω
b
⋀
b
x
This helps define the curvature 2-form, torsion 2-form, and nonmetricity 1-form as potentials of the spin connection , co-frame field , and metric ,
a
ω
b
a
e
g
ab
a
R
b
a
ω
b
a
ω
c
⋀
c
ω
b
1
2
a
R
μνb
μ
dx
⋀
ν
dx
a
T
a
e
1
2
a
T
μν
μ
dx
⋀
ν
dx
Q
ab
g
ab
Q
μab
μ
dx
The Einstein-Hilbert action in differential forms is
S = 2∫x R = ∫ .
4
d
-g
ϵ
abcd
a
e
⋀
b
e
⋀
cd
R
The simplest metric-affine action adds Lagrange multipliers; the most general second-order action in metric-affine gravity contains 28 terms [9,SezginPercacci].
For discrete differential geometry, care must be taken to ensure that appropriate definitions are applied such that the standard differential geometry is found in a continuous limit. Significant progress towards this effort has been made in areas of quantum gravity such as Regge calculus, loop quantum gravity, causal dynamical triangulation, and causal sets.
For hypergraphs, more care is needed to properly define abstractions of of geometric objects. Fortunately, Gorard has demonstrated that the Ollivier-Ricci scalar curvature can be extended to the Riemannian curvature [2]. The same should be possible for the most general affine connection in metric-affine gravity, leading to curvature with contortion and disformation. Next, a systematic study of parallel transport around defects for curvature, torsion, and nonmetricity are demonstrated.
For hypergraphs, more care is needed to properly define abstractions of of geometric objects. Fortunately, Gorard has demonstrated that the Ollivier-Ricci scalar curvature can be extended to the Riemannian curvature [2]. The same should be possible for the most general affine connection in metric-affine gravity, leading to curvature with contortion and disformation. Next, a systematic study of parallel transport around defects for curvature, torsion, and nonmetricity are demonstrated.
Subsection 3.1: Parallel transport for discrete Riemannian curvature
Subsection 3.1: Parallel transport for discrete Riemannian curvature
To implement parallel transport on a Graph, an infinitesimal vector is denoted by a path with one step. For a QuiverGraph, each cardinal is typically associated with a unique direction of propagation. Vectors will be depicted with thin arrows. For instance, an infinitesimal vector at vertex 5 pointing in the x direction leads to vertex 1:
Out[]=
 |
|
 |
|
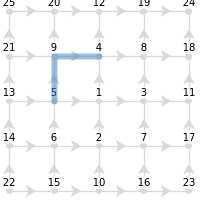
Since parallel transport only probes Riemannian curvature, this crude definition of a tangent vector can be taken to characterize curvature. A more precise notion of a tangent vector will be introduced after torsion is studied more carefully. Parallel transport of a vector involves moving the vector along a path. Paths will be depicted as a thick line. The path “yx” is shown below, which can also be specified as {5,9,4}, allowing convenient support for GraphQuivers and Graphs:
Out[]=
 |
|
Putting these together, parallel transport on a LatticeQuiver with defects can be implemented by translating a path (as a vector) along a path (as a trajectory). The initial vector starts as green, which is parallel transported along a blue path to stop at a red vector:
Out[]=
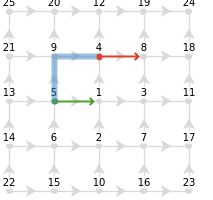 |
|
With the code for displaying parallel transport of vectors on graphs established, the study of anholonomy on lattices with defects can be explored. The wedge disclination is studied to start with the familiar example of Riemannian curvature. For instance, by starting with a vector that points from 6 to 14, parallel transporting about the wedge disclination leads to a rotation such that the final vector points from 6 to 15:
Out[]=
 |
|
 |
|
Recall that X and Y are the negative directions of x and y. From the perspective of the graph above, it is clear that the vector has “rotated” from one cardinal to another. However, the precise angle of rotation is not a geometric quantity presumed on the graph. In principle, Gorard’s study of hypergraphs led to the emergence of Riemannian geometry, implying that natural choices for the lengths and angles could be found. Perhaps additional study is warranted to specify precisely what choices are allowed and/or preferred.
For instance, the square lattice quiver used above leads to a natural suggestion. In principle, Schwartz equalities could be violated; however, choosing conventions that lead to the simplest possible emergent geometry may be taken as a guiding heuristic. At least for the non-defected lattice quiver, a Euclidean grid can be presumed. Independent cardinals need not lead to orthogonal vectors, but this is true if the number of cardinals is equal to the ceiling of the graph dimension (in order to obtain an integer dimension). At least for regular lattice quivers such as the hegagonal grid, the number of cardinals combined with the (integral) dimension leads to the average angle between cardinals, presuming Euclidean geometry. Adding defects lead to some local violations of the Euclidean geometry, which results in gravitational excitations. Comparing arbitrary graphs to some graph known to be abstracted from Euclidean geometry is a helpful way to characterize these gravitational excitations.
Most importantly, the different allowable choices of emergent geometry must lead to the same measurable gravitational effects, leading to a continuous gauge symmetry at each discrete vertex. Metric-affine gravity is needed to study the most general scenarios, as different choices could lead to nonvanishing curvature, torsion, and nonmetricity. In principle, it may be possible to combine general relativity, metric teleparallelism, and symmetric teleparallelism with the appropriate coefficients such that a gravitational wave can be gauge transformed between curvature, torsion, and nonmetricity [PercacciSezgin]. A more systematic analysis of how field redefinitions are associated with these gauge transformations is warranted.
For instance, the square lattice quiver used above leads to a natural suggestion. In principle, Schwartz equalities could be violated; however, choosing conventions that lead to the simplest possible emergent geometry may be taken as a guiding heuristic. At least for the non-defected lattice quiver, a Euclidean grid can be presumed. Independent cardinals need not lead to orthogonal vectors, but this is true if the number of cardinals is equal to the ceiling of the graph dimension (in order to obtain an integer dimension). At least for regular lattice quivers such as the hegagonal grid, the number of cardinals combined with the (integral) dimension leads to the average angle between cardinals, presuming Euclidean geometry. Adding defects lead to some local violations of the Euclidean geometry, which results in gravitational excitations. Comparing arbitrary graphs to some graph known to be abstracted from Euclidean geometry is a helpful way to characterize these gravitational excitations.
Most importantly, the different allowable choices of emergent geometry must lead to the same measurable gravitational effects, leading to a continuous gauge symmetry at each discrete vertex. Metric-affine gravity is needed to study the most general scenarios, as different choices could lead to nonvanishing curvature, torsion, and nonmetricity. In principle, it may be possible to combine general relativity, metric teleparallelism, and symmetric teleparallelism with the appropriate coefficients such that a gravitational wave can be gauge transformed between curvature, torsion, and nonmetricity [PercacciSezgin]. A more systematic analysis of how field redefinitions are associated with these gauge transformations is warranted.
Finally, reconstructing curvature tensors from the transport above is of interest. Since the Riemann curvature tensor is a two-form, the smallest closed-loop paths on graphs naturally trace out analogues of area on a plane. The two-form can be thought of as a bivector in this plane, corresponding to two indices of the Riemann tensor. Since rotational holonomy also picks out another plane of rotation between the initial and final vectors, this corresponds to two other indices, giving four indices of the Riemann curvature tensor. With this definition, curvature would not be localized to the vertices of the graph, but along a 2-face enclosed by the loop.
Utilizing the curvature two-form ,
Utilizing the curvature two-form ,
a
R
b
1
2
a
R
μνb
μ
dx
ν
dx
the indices a and b can be chosen to align with the cardinals x and y as shown in the examples above. Utilization of Regge calculus helps specify how to explicitly find the Riemann tensor values [Regge]. Since this is commonly studied, Regge calculus for discrete torsion is demonstrated more explicitly next.
Subsection 3.2: Autoparallel for discrete torsion
Subsection 3.2: Autoparallel for discrete torsion
Strictly speaking, autoparallel transport is needed to probe torsion. However, since the starting point is not from an affine connection, the distinction of parallel vs autoparallel transport on discrete graphs must be understood. The line dislocation in 2D is the quintessential example of a defect with torsion.
Demonstrating torsion along a dislocation line helps further understand the interpretation of a tangent vector on a discrete manifold or a (hyper-)graph. Start by considering a vector from 6 to 14 on the dislocation defect example:
Demonstrating torsion along a dislocation line helps further understand the interpretation of a tangent vector on a discrete manifold or a (hyper-)graph. Start by considering a vector from 6 to 14 on the dislocation defect example:
Out[]=
 |
|
The torsion tensor is defined as the antisymmetric component of the affine connection, which relates directly to the noncommutativity of the spacetime translation (energy-momentum) operators. Translating by the cardinals xy starting at 6 clearly differs from translating by yx, as yx is not allowed. Instead, consider how xyy vs yyx lead to a different point (12 vs 4) to indicate the presence of torsion:
Out[]=
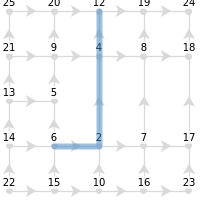 |
|
 |
|
However, if 14 is associated with the arrowhead of a tangent vector originating from 6, the arrowhead’s transport is commutative, as following the same path does not partially enclose the defect:
Out[]=
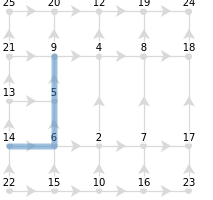 |
|
 |
|
Parallel transport in a loop cannot directly probe torsion, as it only includes the Levi-Civita connection. Similarly, transporting the base of a vector along the base manifold about a loop can never result in a translation of a vector, as it is constructed to return to the same position:
Out[]=
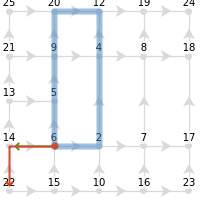 |
|
 |
|
In order to appropriately quantify torsion, a different notion of a “cardinal loop” can be introduced in order to characterize the noncommutativity of translations such that in the absence of torsion, the path taken forms a loop. For instance, following xyXYY starting from 6 is a closed path, but the lattice quiver is defined such that “xyXY” is a loop, leading to an excess of Y to be interpreted as the Burger’s vector:
Out[]=
 |
|
The autoparallel transport of the true tangent vector is shown above. Once again, the origin of the vector is transported along a loop, but then shifted based on the residual Burger’s vector Y leftover from removing the “cardinal loop”. The arrowhead of the final vector is left unchanged from the original path, as there is no torsion encapsulated by the path of the arrowhead. A more precise explanation for why this occurs will be addressed after the following example. Regge Calculus in metric teleparallelism addressed the notion of discrete torsion [Pereira], which found the torsion tensor in terms of the flux of dislocation lines Φ = ρ through a loop area in terms of an antisymmetric unit tensor normalized as = 2, with a defect density ρ for four dimensions. The closure failure given by = Φ is in terms of the Burger’s vector , which leads to the torsion tensor ,
1
2
U
αβ
αβ
S
αβ
S
αβ
U
αβ
U
U
αβ
B
μ
b
μ
b
μ
T
μαβ
T
μαβ
1
2
U
αβ
b
μ
where the torsion tensor is found to not depend on the area of the loop taken. Care must be taken with reading their work, however, since the notion of parallel transport vs autoparallel was not distinguished, which is a common point of confusion.
For the two-dimensional example above, however, the area is characterized by a scalar, such that Φ = ρS for the 2D area of the surface S. The antisymmetric unit tensor is still needed to get the torsion 3-tensor, which matches intuition from the differential forms approach of looking at torsion as a 2-form. The Burger’s vector clearly denotes the third residual index of the torsion 3-tensor, as this is for local coordinates associated with the tangent space rather than global coordinates of the manifold.
The only way for Φ = ρS to be satisfied such that the system has one dislocation line, it is clear that the dislocation density ρ vanishes everywhere except within the “pentagon” found via transporting around vertices {6,2,4,9,5}. This is because increasing the area of the loop does not lead to a larger Burger’s vector,
For the two-dimensional example above, however, the area is characterized by a scalar, such that Φ = ρS for the 2D area of the surface S. The antisymmetric unit tensor is still needed to get the torsion 3-tensor, which matches intuition from the differential forms approach of looking at torsion as a 2-form. The Burger’s vector clearly denotes the third residual index of the torsion 3-tensor, as this is for local coordinates associated with the tangent space rather than global coordinates of the manifold.
The only way for Φ = ρS to be satisfied such that the system has one dislocation line, it is clear that the dislocation density ρ vanishes everywhere except within the “pentagon” found via transporting around vertices {6,2,4,9,5}. This is because increasing the area of the loop does not lead to a larger Burger’s vector,
Out[]=
 |
|
Therefore, the dislocation density is zero everywhere except around the “pentagon”, which has a density of 1. Similarly, the torsion tensor is zero everywhere except on the pentagon. By presuming the cardinals {x,y} are along the x and y directions, the torsion on the “pentagon” is found to be
T
xαβ
T
yαβ
-
1
2
U
αβ
U
αβ
0 | 1 |
-1 | 0 |
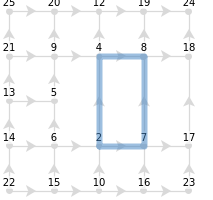
where an antisymmetric = 2 in two dimensions is uniquely determined up to a sign of -1. Switching this sign can be reconciled by setting Φ = -ρS or absorbing the -1 into the dislocation density, as the extra-dimensional analogue of this equation contained . Setting this factor of -1 is truly conventional, as removing a dislocation line from the right is indistinguishable from adding a dislocation line from the left. Finally, the autoparallel transport of a vector pointing from 2 to 6 along the xyXY loop does not lead to torsion, but it at first may seem to contain curvature and nonmetricity due to the remnant of the the torsion for the arrowhead’s path. Taking a closed path xyXY on the base manifold closes when starting from 2, but not 6:
αβ
U
U
αβ
U
αβ
Out[]=
 |
|
 |
|
With the definition of a tangent vector provided thus far, the tangent vector pointing from 2 to 6 may seem to end by pointing from 2 to 5, which seemingly results in curvature and nonmetricity since the tangent vector rotates and changes length:
Out[]=
 |
|
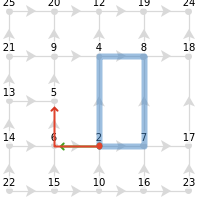
The definition of autoparallel transport of a tangent vector on discrete quiver graphs is chosen as follows: 1) An initial tangent vector is specified as a path on the base manifold that points from the vector’s “origin” to its “arrowhead”. 2a) A loop is designated on the base manifold, which acts as the path for the origin of the vector. 2b) Another path is found by following the same cardinal directions starting at the vector’s arrowhead. Additionally, the closed loop closest to this path is found by either removing unnecessary steps or adding the minimal number of steps that closes the loop. 3a) The tangent vector’s origin is translated along the first loop from the base manifold corresponding to the path of interest and then translated based on the cadinal noncommutativity of that closed path. 3b) The tangent vector’s arrowhead is translated along the second path and then translated by any noncommutativity picked up by the closed loop for the arrowhead. A more careful description of this step-by-step algorithm should be described in terms of pushbacks and pullforwards between the base manifold and tangent space. This can be overlooked, as the base manifold and tangent space manifold are gauge fixed to have the same geometric description. In order to obtain the most structure as possible from a hypergraph in WM, the tangent space manifold is constrained to have the same geometric structure as the base space manifold. This can be seen as related to Born’s reciprociy of phase space, Smolin et al.’s relative locality, or Kroner’s notion of strain and stress space [8]. With this definition of the autoparallel transport of a tangent vector along a graph with labelled edges (such as a quiver graph with cardinals), transporting the vector from 2 to 6 around the xyXY loop leads to vanishing curvature, torsion, and nonmetricity:
Out[]=
 |
|
 |
|
To reiterate, the arrowhead of the tangent vector starts at 6 and then is transported along the xyXY path leading back to 5 to match the original path’s cardinal translations, but an additional step Y is needed to close the loop due to the enclosed dislocation density of the arrowhead’s xyXYY loop.
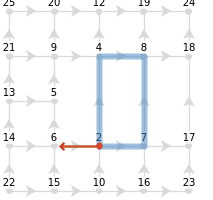
This definition still leads to the same value of torsion for the loop starting at vertex 6 that encapsulates the defect with the vector, since the arrowhead’s path does not encapsulate any torsion and therefore is not further corrected:
This definition still leads to the same value of torsion for the loop starting at vertex 6 that encapsulates the defect with the vector, since the arrowhead’s path does not encapsulate any torsion and therefore is not further corrected:
Out[]=
 |
|
Subsection 3.3: Autoparallel for discrete nonmetricity
Subsection 3.3: Autoparallel for discrete nonmetricity
Transport to detect the most general notion of nonmetricity is different than torsion and curvature, since the nonmetricity tensor is a 1-form, while curvature and torsion are a 2-form. In other words, anholonomic loops are ideal characterizations of 2-forms, as a loop leads to a notion of area. Anholonomic loops can characterize an aspect of nonmetricity, as it is conceivable that the length of a vector could change after traversing a path. However, this type of nonmetricity seems more exotic, unless the length of vectors should change over time due to a difference between quantum and cosmological clocks, as suggested by Dirac. A more general characterization of nonmetricity is worth understanding. Since nonmetricity is a 1-form, a 1-way path may be studied rather than a loop. Measuring how the vector changes length over that path characterizes nonmetricity [16]. However, experimentally observing this type of nonmetricity may not be possible, as one can only measure two-way speeds of light, rather than the one-way speed.
Einstein studied aspects of nonmetricity between 1912-1914. As it turned out, the equivalence principle was expounded upon in the 1915 formulation commonly studied today. However, Einstein’s theory of general relativity is at times argued to be the principles of the theory rather than the specific formulation. For instance, Dicke revisited Einstein’s earlier work and made it self-consistent by adding a scalar field, which is the most common approach in cosmology. Additionally, Lyra geometry replaces nonmetricity for a scalar field. Weyl’s conformal gravity also investigated nonmetricity, which was pointed out by Schrodinger in 1937 to have aspects that are indistinguishable from torsion with respect to autoparallels, which motivates why Weyl gravity can be accepted. Nonminimal coupling of conformal gravity seems to give a unitary and renormalizable theory of gravity that pairs with the standard model, but additional research is needed to fully understand the ideal quantum gravitational formulation [12]. The geometrical trinity of gravity makes this more clear, as there are differing geometric interpretations that lead to dynamics in Einstein’s field equations [16].
Nonmetricity measures the deviation of length along a single path [Damianos]. The metric tensor gives the inner product of two vectors and :
g
μν
μ
a
ν
b
a.b = .
g
μν
μ
a
ν
b
While Riemannian spaces have (a.b) = 0, nonvanishing nonmetricity results in
D
dλ
D
dλ
-
Q
αμν
D
α
x
dλ
μ
a
ν
b
The autoparallel transport as defined in the previous section overlooked the full details for specifying nonmetricity, but the interpretation becomes clear after reviewing the image shown in Subsubsection 2.2.3. With respect to autoparallel transport, an aspect of nonmetricity is indistinguishable from torsion [Damianos].
Section 4: Discrete Bundle Gerbes
Section 4: Discrete Bundle Gerbes
The notion of membranes has its origins in supergravity, which is a gauge theory of gravity. The 11-dimensional supermembrane theory of 1987 was revisited by Townsend in 1995, which contained overlapping content with Witten’s introduction of M(embrane)-theory [Duff,Bergshoeff,Townsend,Witten]. However, no-go theorems have left the community in a difficult state. On the one hand, the Coleman-Mandula theorem seems to imply that supersymmetry is necessary for quantum field theory with a finite spectrum with Poincare invariance. On the other hand, Nahm argued that 11-dimensional supergravity is maximal, yet it is known that this theory cannot quite lead to the standard model spectrum at low energies. This makes heterotic string theory within M-theory to seem like the only chance left. However, supergravity is the low-energy limit of other string theories, but the apparent lack of supergravity for heterotic strings makes the low-energy theory of string theory difficult to predict. Furthermore, the mathematics of M-theory is not yet complete, as the membranes require a notion of non-Abelian bundle gerbes. The Wolfram Model’s focus on discrete differential geometry motivates the exploration of discrete bundle gerbes, as this is a current area of active research in quantum gravity.
Bundle gerbes generalize the notion of fiber bundles. They are studied within the context of higher gauge theory in the context of category theory. Kleinert’s study of multivalued fields for defects also led to exotic forms of gauge symmetry [Kleinert]. A multivalued vector field fails to satisfy an integrability condition,
Bundle gerbes generalize the notion of fiber bundles. They are studied within the context of higher gauge theory in the context of category theory. Kleinert’s study of multivalued fields for defects also led to exotic forms of gauge symmetry [Kleinert]. A multivalued vector field
ξ
k
-≠0
∂
i
∂
j
∂
j
∂
i
ξ
k
which is the definition of spacetime torsion tensor for small translations [10]. The simplest example of a gerbe relates to the parallel transport of the Kalb-Ramond antisymmetric two-form, which was proven by Scherk and Schwarz to be identical to spacetime torsion [ScherkSchwarz]. For this reason, it is conjectured that Kleinert’s gauge theory of defects via mutlivalued fields is related to the higher gauge theory of bundle gerbes, as the multivalued nature of the field leads to a topological index. Additionally, bundle gerbes have been studied in relationship to twisted K-theory; the twisted K-groups are torsion with a twisted Chern characteristic [Bouwknegt,Carey].
It is typically stated that torsion is non-propagating in spacetime. Nevertheless, it is studied in string theory and supergravity, as the torsion is needed inside matter to reconcile quantum spin [Ortin]. Supergravity could be thought of as Poincare gauge gravity in matter, yet constrained to Einstein-Cartan theory in vacuum. The 3-form in D=11 N=1 supergravity is sourced by a 2-brane, which leads to a 2-form Kalb-Ramond field sourced by a string in D=10. This is a higher U(1) gauge field making contact with Deligne cohomology.
The notion of a gerbe comes from understanding the trajectories of p-branes, where a particle is a 0-brane, while a string is a 1-brane. The particle follows a 1-dimensional path, while the string traces out a 2-dimensional trajectory. In light of the 3-dimensional aspect of space, 3-branes are attractive candidates for unified geometrodynamics, as this has a chance to lead to particle-like excitations that could be made from the same stuff as spacetime itself [RandallSundrum]. Independent of string and membrane theories, Einstein-Cartan theory with torsion has found notions of extended objects [Poplawski]. Additionally, Ne’eman was a pioneer of extendons as well as spinors in metric-affine gravity [9].
The D3 brane of D=3+1 type IIB theory leads to a notion of AdS5/CFT4 as studied in the Randall-Sundrum model [RandallSundrum]. The type IIB superalgebra is not described by M-theory, but rather Vafa’s 12-dimensional F-theory [Vafa]. Standard model phenomenology has been more successful with F-theory than M-theory [Heckman]. Furthermore, 12-dimensional supergravity has been explored in a manner that does not apply to Nahm’s no-go theorem [NIshino]. Still, a lack of understanding M-theory also leads to a lack of understanding F-theory. Bars demonstrated that a 14-dimensional superalgebra unifies all of the supergravity theories more directly than M-theory can, however, the origins of heterotic string theory must go beyond D=25+1 [Bars]. Recently, the author found an infinite class of new superalgebras with fermions to arbitrarily higher dimensions. The utilization of a nested braneworld model allows for the possibility of a 3-brane inside an 11-brane inside a 27+3-dimensional theory, which is the only known candidate to describe an origin for M-theory, F-theory, and the recently conjectured A-theory in D=11+3 dimensions [Rios].
A brief outline for the first attempt of connecting membranes and gerbes to the Wolfram Model is discussed next. Additionally, a sketch of the flow from geometry to cardinal quivers to hypergraphs is depicted. To start, any discrete geometric spacetime manifold presumably can be abstracted to a lattice quiver with various cardinal edges instead of vectors with well-defined direction. For membranes sourcing tensorial potential fields, considering a bundle of multiple paths as a tensor may help. Tensor fields may allow for a representation in terms of hyperedges, as the hyperedges can span multiple directions similar to a tensor. However, the parallel transport of these branes seemingly leads to a bundle of paths. Representing discretized gerbes via a causal multiway graph seems promising for quantum transport.
ξ
k
It is typically stated that torsion is non-propagating in spacetime. Nevertheless, it is studied in string theory and supergravity, as the torsion is needed inside matter to reconcile quantum spin [Ortin]. Supergravity could be thought of as Poincare gauge gravity in matter, yet constrained to Einstein-Cartan theory in vacuum. The 3-form in D=11 N=1 supergravity is sourced by a 2-brane, which leads to a 2-form Kalb-Ramond field sourced by a string in D=10. This is a higher U(1) gauge field making contact with Deligne cohomology.
The notion of a gerbe comes from understanding the trajectories of p-branes, where a particle is a 0-brane, while a string is a 1-brane. The particle follows a 1-dimensional path, while the string traces out a 2-dimensional trajectory. In light of the 3-dimensional aspect of space, 3-branes are attractive candidates for unified geometrodynamics, as this has a chance to lead to particle-like excitations that could be made from the same stuff as spacetime itself [RandallSundrum]. Independent of string and membrane theories, Einstein-Cartan theory with torsion has found notions of extended objects [Poplawski]. Additionally, Ne’eman was a pioneer of extendons as well as spinors in metric-affine gravity [9].
The D3 brane of D=3+1 type IIB theory leads to a notion of AdS5/CFT4 as studied in the Randall-Sundrum model [RandallSundrum]. The type IIB superalgebra is not described by M-theory, but rather Vafa’s 12-dimensional F-theory [Vafa]. Standard model phenomenology has been more successful with F-theory than M-theory [Heckman]. Furthermore, 12-dimensional supergravity has been explored in a manner that does not apply to Nahm’s no-go theorem [NIshino]. Still, a lack of understanding M-theory also leads to a lack of understanding F-theory. Bars demonstrated that a 14-dimensional superalgebra unifies all of the supergravity theories more directly than M-theory can, however, the origins of heterotic string theory must go beyond D=25+1 [Bars]. Recently, the author found an infinite class of new superalgebras with fermions to arbitrarily higher dimensions. The utilization of a nested braneworld model allows for the possibility of a 3-brane inside an 11-brane inside a 27+3-dimensional theory, which is the only known candidate to describe an origin for M-theory, F-theory, and the recently conjectured A-theory in D=11+3 dimensions [Rios].
A brief outline for the first attempt of connecting membranes and gerbes to the Wolfram Model is discussed next. Additionally, a sketch of the flow from geometry to cardinal quivers to hypergraphs is depicted. To start, any discrete geometric spacetime manifold presumably can be abstracted to a lattice quiver with various cardinal edges instead of vectors with well-defined direction. For membranes sourcing tensorial potential fields, considering a bundle of multiple paths as a tensor may help. Tensor fields may allow for a representation in terms of hyperedges, as the hyperedges can span multiple directions similar to a tensor. However, the parallel transport of these branes seemingly leads to a bundle of paths. Representing discretized gerbes via a causal multiway graph seems promising for quantum transport.
Section 5: Concluding remarks
Section 5: Concluding remarks
The holonomy of lattice quiver defects was explored in an attempt to bring a discrete formulation of metric-affine gravity to the Wolfram Model. Due to time constraints, brief comments rather than demonstrations are provided to transition away from lattice quivers and towards hypergraphs. Both objects are abstract and do not have precisely defined notions of geometry. However, both lead to notions of combinatorial graph distance. In the presence of defects, it was shown how the conventions chosen for interpretting length on the same graph lead to different geometric quantities. Despite the fact that these interpretations are different, it does not imply that the same graph with different conventions will lead to different physics, as demonstrated by the geometrical trinity of gravity [16].
The exploration of lattice quiver defects demonstrated that one may count graph distance before or after the defect is added. This calibration of length concept can be applied to hypergraphs in the Wolfram model. If spacetime expansion and evolution is dictated by rewrite rules, then the local graph distance between two adjacent nodes would increase over time, presuming that the rewrite rule leads to a new node between the two adjacent nodes. While spacetime does expand, the planets within solar systems do not spread apart over time. Therefore, it helps to open up to multiple calibrations of rulers for hypergraph evolution. A new class of combinatorial definitions of length can be found that lead to fractional distances rather than integers.
The exploration of lattice quiver defects demonstrated that one may count graph distance before or after the defect is added. This calibration of length concept can be applied to hypergraphs in the Wolfram model. If spacetime expansion and evolution is dictated by rewrite rules, then the local graph distance between two adjacent nodes would increase over time, presuming that the rewrite rule leads to a new node between the two adjacent nodes. While spacetime does expand, the planets within solar systems do not spread apart over time. Therefore, it helps to open up to multiple calibrations of rulers for hypergraph evolution. A new class of combinatorial definitions of length can be found that lead to fractional distances rather than integers.
Keywords
Keywords
◼
Metric-affine gravity
◼
elasticity theory
◼
Dual gauge theory of defects
◼
Higher gauge theory
◼
Discrete bundle gerbes
◼
Discrete matrix membrane models
Acknowledgment
Acknowledgment
Thanks to the mentorship of Jon Lederman, discussion with Taliesin Beynon, Xerces Arsiwalla, Jonathan Gorard, as well as the TAs, students, and staff at the 2021 Wolfram Summer School. This work was also inspired by work and discussion related to a quasicrystalline matrix model of elasticity with Klee Irwin, Ray Aschheim, and the scientists at Quantum Gravity Research in Topanga, CA, USA.
References
References
◼
◼
[2] J. Gorard, “Some Relativistic and Gravitational Properties of the Wolfram Model”, (2020); ibid, “Hypergraph Discretization of the Cauchy Problem in General Relativity via Wolfram Model Evolution”, (2021), arXiv:2102.09363 [gr-qc].
◼
◼
[4] F. Brandao, et al., "The second laws of quantum thermodynamics", PNAS 112, 3275, (2015), arXiv:1305.5278 [quant-ph].
◼
[5] X. D. Arsiwalla, J. Gorard, H. Elshatlawy, “Homotopies in Multiway (Non-Deterministic) Rewriting Systems as n-Fold Categories”, (2021), arXiv:2105.10822v1 [math.CT].
◼
[6] J. C. Baez & J. Huerta, "An invitation to higher gauge theory", Gen. Rel. and Grav. 43, 2335-2392, (2011), arXiv:1003.4485 [hep-th].
◼
[Patarroyo] K. Patarroyo, “Defect movement in lattice rewriting systems”, Wolfram Winter Summer School, (2021).
◼
[Kleman] M. Kleman & J. Friedel, “Disclinations, dislocations and continuous defects: a reappraisal”, Rev. Mod. Phys. 80, 61-115, (2008), arXiv:0704.3055v1 [cond-mat.soft]. M. Kleman, “Forms of Matter and Radiation”, IPGP report # 2516, arXiv:0905.4643v2 [gr-qc].
◼
[Millette] P. A. Millette, “Bosons and Fermions as Dislocations and Disclinations in the Spacetime Continuum”, Prog. in Phys. 14, 1, (2018); ibid, “Elastodynamics of the Spacetime Continuum”, American Research Press, (2017).
◼
[7] G. Chapline, E. Hohlfeld, R. B. Laughlin, & D. I. Santiago, “Quantum phase transitions and the breakdown of classical general relativity", Phil. Mag. B-Phys. of Cond. Matt. Stat. Mech. Elec. Opt. and Mag. Prop., 81 (3), 235–254, (2001).
◼
[8] E. Kroner, "Stress Space and Strain Space in Continuum Mechanics", Phs. Stat. Solid. B 144, 1: 39-44, (1987).
◼
[Kroner] According to Hehl et al. 1995, Kroner worked out that zero-dimensional defects correspond to nonmetricity in the condensed matter context, but nobody has elaborated on the gravitational interpretation. The author has not yet found any papers in English that discuss this work.
◼
[9] F. W. Hehl, G. D. Kerlick, P. Von der Heyde, “On a new metric affine theory of gravitation”, Phys. Lett. B 63 (4), 16: 446-448, (1976); F.Hehl, J. McCrea, E. Mielke, Y. Ne’eman, “Metric-affine gauge theory of gravity: field equations, Noether identities, world spinors, and breaking of dilaton invariance”, Phys. Rep. 258, 1-171, (1995), arXiv:9402012 [gr-qc].
◼
[10,Kleinert] H. Kleinert, "Multivalued Fields in Condensed Matter, Electromagnetism, and Gravitation", World Scientific, Singapore, (2008).
◼
[11] N. Poplawski, “Four-fermion interaction from torsion as dark energy”, Gen. Rel. Grav. 44: 491-499, (2012), arXiv:1102.5667 [gr-qc].
◼
[12] de Cesare, “Cosmological consequences of Quantum Gravity proposals”, King’s College PhD Thesis, (2017), arXiv:1804.02262 [gr-qc].
◼
[13] Yo & Nester, "Symmetric Teleparallelism", Chin. J. Phys. 37 113, (1998), arXiv:9809049 [gr-qc].
◼
[14] Z. Bern, H. Chi, L. Dixon, & A. Edison, “Two-Loop Renormalization of Quantum Gravity Simplified”, Phys. Rev. D 95, 046013, (2017), arXiv:1701.02422 [hep-th].
◼
[Wang2021] P. Wang, et. al., “Derive Lovelock Gravity from String Theory in Cosmological Background”, JHEP 2105, 218, (2021), arXiv:2012.13312 [hep-th].
◼
[15] C. Cheung & G. N. Remmen, "Twofold Symmetries of the Pure Gravity Action", JHEP 1701, 104, (2017), arXiv:1612.03927 [hep-th].
◼
[16] J. Beltran Jimenez, L. Heiseinberg, & T. S. Koivisto, "The Geometrical Trinity of Gravity", Universe 5 (7), 173, (2019), arXiv:1903.06830 [hep-th].
◼
[17] Y. M. Cho, “Einstein Lagrangian as the translational Yang-Mills Lagrangian”, Phys. Rev. D 14, 2521, (1976).
◼
[18] C. Cheung & J. Mangan, “Scattering Amplitudes and the Navier-Stokes Equation”, CALT-TH 2020-044, arXiv:2010.15970v1 [hep-th].
◼
[DoubleCopy] Z. Bern, J. J. Carrasco, H. Johansson, “Perturbative Quantum Gravity as a Double Copy of Gauge Theory”, Phys. Rev. Lett. 105 (6), (2010). arXiv:1004.0476 [hep-th].
◼
[Poplawski] N. Poplawski, “Noncommutative momentum and torsional regularization”, Found. Phys. 50, 900, (2020), arXiv:1712.09997 [gr-qc].
◼
◼
[Truini] P. Truini, A. Marrani, M. Rios, K. Irwin, “Space, Matter and Interactions in a Quantum Early Universe. Part I : Kac-Moody and Borcherds Algebras”, arXiv:2012.10227 [gr-qc]; ibid., “Space, Matter and Interactions in a Quantum Early Universe. Part II : Superalgebras and Vertex Algebras”, arXiv:2012.10248 [gr-qc].
◼
◼
[Schreiber] J. Huerta & U. Schreiber, “M-theory from the Superpoint”, Lett. Math. Phys. 108, 2695–2727, (2018), arXiv:1702.01774 [hep-th].
◼
[Dzhunushaliev] V. Dzhunushaliev, V. Folomeev, M. Minamitsuji, “Thick brane solutions”, Rept. Prog. Phys. 73, (2010), arXiv:0904.1775 [gr-qc].
◼
[Regge] T. E. Regge, “General relativity without coordinates”, Nuovo Cimento 19 (3): 558-571, (1961).
◼
[Pereira] J. G. Pereira, T. Vargas, “Regge Calculus in Teleparallel Gravity”, Class. Quant. Grav. 19, 4907-4816, (2002), arXiv[0208036] [gr-qc].
◼
[Damianos] I. Damianos, “Metric-Affine Gravity and Cosmology/ Aspects of Torsion and Non-metricity in Gravity Theories”, Aristotle University Thesis, arXiv:1902.09643 [gr-qc].
◼
◼
[SezginPercacci] R. Percacci & E. Sezgin, “A New Class of Ghost and Tachyon Free Metric Affine Gravities”, Phys. Rev. D 101, 084040, (2020), arXiv:1912.01023 [hep-th].
◼
[Maldacena] J. Maldacena, “The Large N Limit of Superconformal Field Theories and Supergravity”, Adv. Theor. Math. Phys. 2: 231-252, (1998), arXiv:9711200 [hep-th].
◼
[Duff] M. J. Duff, P. S. Howe, T. Inami, & K. S. Stelle, “Superstrings in D=10 from supermembranes in D=11”, Phys. Lett. B 191 (1-2) 4: 70-74, (1987).
◼
[Bergshoeff] E. Bergshoeff, E. Sezgin, & P. K. Townsend, “Supermembranes and eleven-dimensional supergravity”, Phys. Lett. B 189, (1-2) 30: 75-78, (1987); ibid., “Properties of the eleven-dimensional supermembrane theory”, Ann. Phys. 185, (2) 1: 330-368, (1988).
◼
[Townsend] P. K. Townsend, “The eleven-dimensional supermembrane theory revisited”, Phys. Lett. B 350, 2 11: 184-188, (1995).
◼
[Witten] E. Witten, “String Theory Dynamics in Various Dimensions”, Nucl. Phys. B 443: 85-126, (1995), arXiv:9503124 [hep-th].
◼
[ScherkSchwarz] J. Scherk & J. H. Schwarz, “Dual models and the geometry of space-time”, Phys. Lett. B 52 (3) 14: 347-350, (1974).
◼
[Bouwknegt] P. Bouwknegt, et. al., “Twisted K-theory and K-theory of bundle gerbes”, Commun. Math. Phys. 228: 17-49, (2002), arXiv:0106194 [hep-th].
◼
[Carey] A. L. Carey, J. Mickelsson, & B. Wang, “Differential twisted K-theory and applications”, Jour. Geom. Phys. 59 (5): 632-653, (2009).
◼
◼
[RandallSundrum] L. Randall, R Sundrum, “Large Mass Hierarchy from a Small Extra Dimension” Phys. Rev. Lett. 83 (17): 3370-3373, (1999), arXiv:9905221 [hep-ph].
◼
[Vafa] C. Vafa, “Evidence for F-theory”. Nucl. Phys. B. 469 (3): 403–415, (1996), arXiv:9602022 [hep-th].
◼
[Heckman] J. J. Heckman, C. Vafa, “Flavor Hierarchy From F-theory”, Nucl. Phys. B 837: 137-151, (2010), arXiv:0811.2417 [hep-th].
◼
[Nishino] H. Nishino, “Supergravity in 10 + 2 Dimensions as Consistent Background for Superstring”, Phys. Lett. B 428: 85-94, (1998), arXiv:9703214 [hep-th].
◼
[Bars] I. Bars, “A case for 14 dimensions”, Phys. Lett. B 403: 257-264, (1997), arXiv:9704054 [hep-th].
◼
[Rios] M. Rios, A. Marrani, D. Chester, “Exceptional Super Yang-Mills in D=27+3 and Worldvolume M-Theory”, Phys. Lett. B, 808, (2020), arXiv:1906.10709 [hep-th]; ibid. “Monstrous M-theory”, arXiv:2008.06742 [hep-th].
Cite this as: David Chester, "Towards Discretizing Metric-Affine Gravity via Elastic Hypergraphs" from the Notebook Archive (2021), https://notebookarchive.org/2021-07-60oanhf
Download
