Essays, Posts & Presentations

[WSS20] Text Generation Using GANs

Suman Sigdel

Author

Suman Sigdel

Title

[WSS20] Text Generation Using GANs

Description

A comparision between Generative Adversarial Networks and RNN for text generation.

Text Generation using GANs

Suman Sigdel

Bennington College

Goal : Generative Adversarial Networks have been used mostly for image data and are known to produce data that closely match the given input eg. deep fakes. Text generation is an area in which GANs are used less given the discrete structures of text. We believe that CNN based GAN architecture used for images can also be used in text generation to generate comparable results to that of RNN models. A comparison between GANs and RNNs will be made to draw a clear distinction between the results they produce using n-gram distributions as a performance metric.

Results : Comparing the two text generation models, using euclidean distance of n-gram as a metric, we found that the text generated by the GAN model (for shorter lengths) is better than the RNN model for multiple n-grams. Although the unstable nature of GANs might affect it’s performance, we believe that through multiple fine tuning methods and proper model selection using the n-gram metric, the GAN model’s performance can be further improved.

Application :
Text generation models can be used for : product names, naming new chemicals, naming new startups etc.

Wolfram Community Post (material for blog post)

IntroductionGenerative Adversarial Networks or GANs are most commonly known to produce results that are almost indistinguishable from the real dataset eg. deep fakes. GANs consist of two neural networks, Generator and Discriminator which compete in an adversarial zero sum game in order to generate plausible examples. The generator never sees the actual training data and only gets data from a latent space, to which it assigns meaning with the help of the discriminator. The discriminator is trained with samples generated by the generator and the samples from the training dataset and learns to classify between real and fake data. The two models operate in a zero sum game in a sense that when the discriminator successfully classifies real and fake samples, it is rewarded with no updates made to the model parameters, however the generator is penalized with large updates. Similarly, when the generator generates plausible examples, only the discriminator’s parameters are updated. Large amounts of research have been done with GANs for image translation, generation of deep fakes and data augmentation, but GANs application in text and NLP is an area that is less explored.AimIn this project, I will be applying GANs for text generation and will be comparing the results with existing Recurrent Neural Networks. This project aims to show that through adversarial training better text generation results can be achieved which is comparable to existing RNN models. This post is divided into 4 sections. In the first section, I will explain the metric that will be used to measure the performance of the text generation models. I will then train existing RNN language model with chemical and company names and show it’s performance. I will then explain the GAN architecture that was used for text generation and will show it’s performance while generating texts and finally will make a comparison between the performance of GAN and RNN model.

1. Performance Metric

Normalizing text

To compare the different model performances, we will be finding the euclidean distance of n-grams between text generated from two models. The initial step will be to remove special characters and diacritics from the real dataset. The following code accomplishes this goal by using a combination of StringReplace, ToLowerCase and Remove Diacritics functions to normalize the characters in the dataset.

In[]:=

normalizeText[s_] := ToLowerCase @ RemoveDiacritics @ StringReplaces, WordBoundary~~(WordCharacter..)~~".""",(*Remove "mr.","jr.",...*) "♂""♀""",(*Remove gender hints*) "-""-""'"" ",(*Remove very rare characters*) DigitCharacter"" ,(*Remove very rare characters*) "("|")"  "",(*Remove Brackets*) "%"":"  "",(*Remove Colons and %*) "ʻ" "‘" "",(*Remove other special characters*) "`""", " "  "", "=""?""", "}""{" ""}

Computing n-grams

The next step is to create a lookup table for the different characters so that we can put them in their respective coordinates in the sparse array. The following code makes an association that maps characters and special tokens to an unique point.

In[]:=

characters = AssociationThread[ Join[CharacterRange["a","z"], {" ", StartOfString, EndOfString}]  Range[29]];

A function to compute n-grams is created which computes n-gram for a given wordlist and puts frequencies of each n-gram in a SparseArray. A sparse-array is chosen for faster computation for higher “n” in the n-grams.

In[]:=

computeNGrams[texts_, n_] := Block[{ngrams}, ngrams = Flatten[ Function[Partition[#, n, 1]] /@ Function[Join[{StartOfString}, Characters[#], {EndOfString}]] /@ normalizeText[texts], 1 ]; (* Convert to indices *) ngrams = Map[Lookup[characters, #]&, ngrams]; (* Counts *) ngrams = Normal[N @ Counts[ngrams] / Length[ngrams]]; (* Fill SparseArray *) SparseArray[ngrams, Table[Length[characters],n]]];

Example

Running the following code will normalize chemical names.

In[]:=

chemicalNames = EntityValue[EntityList["Chemical"],"Name"];chemicalNames = Select[c,StringMatchQ[#,CharacterRange["A","z"]..]&];tennormalizednames = Take[normalizeText@chemicalNames,10]

Out[]=

{hydrogen,helium,deuterium,lithium,beryllium,boron,diamond,graphite,borane,methane}

The following code will then compute the 1 and 2 grams and map their indices to respective normalized occurrences in a SparseArray.

computeNGrams[tennames,1]computeNGrams[tennames,2]

Out[]=

SparseArray

Specified elements: 18

Dimensions: {29}

Default: 0

Density: 0.621

Elements:

{28}

0.109

{8}

0.0543

{25}

0.0217

{4}

0.0435

⋮



Out[]=

SparseArray

Specified elements: 52

Dimensions: {29,29}

Default: 0

Density: 0.0618

Elements:

{1,13}

0.0122

{1,16}

0.0122

{1,14}

0.0244

{2,5}

0.0122

⋮



Euclidean Distance between n-gram distributions

We then compute the euclidean distance between the distributions of n-grams in the dataset and generated text. The findEuclideanDistance computes the euclidean distance between two n gram distributions. The DistancesofNgrams function takes the generator and the training dataset to find the euclidean distance between n-gram distributions (between generated and training dataset) where n goes from 1 to 5.

In[]:=

findEuclideanDistance[ngram1_,ngram2_]:= EuclideanDistance[Flatten@ngram1,Flatten@ngram2]DistancesofNgrams[generator_, dataset_]:= Table[findEuclideanDistance[computeNGrams[generator@latentGeneration[1000],n], computeNGrams[dataset,n]],{n,1,5}]

Using this metric we will be able to compare the GAN model as well as the RNN model. In addition, we will be able to see how the euclidean distance converges as the GAN model is trained.

( Murgue T., de la Higuera C. (2004) Distances between Distributions: Comparing Language Models. In: Fred A., Caelli T.M., Duin R.P.W., Campilho A.C., de Ridder D. (eds) Structural, Syntactic, and Statistical Pattern Recognition. SSPR /SPR 2004. Lecture Notes in Computer Science, vol 3138. Springer, Berlin, Heidelberg)

2. RNN Model

The RNN model that will be used for comparison is the pretrained
Wolfram English Character-Level Language Model V1.
The following is the architecture of this model :

In[]:=

NetModel["Wolfram English Character-Level Language Model V1"]

Out[]=

NetChain



Input

string

vector of

indices

(range: 1..97)

EmbeddingLayer

matrix

(size:

×97)

DropoutLayer

matrix

(size:

×97)

GatedRecurrentLayer

matrix

(size:

×512)

GatedRecurrentLayer

matrix

(size:

×512)

GatedRecurrentLayer

matrix

(size:

×512)

SequenceLastLayer

vector

(size: 512)

LinearLayer

vector

(size: 97)

SoftmaxLayer

vector

(size: 97)

Output

class



We will now train the RNN model on 3 different datasets and measure their respective euclidean distance for 1 to 5 n-grams.

1. Chemical Names

The following code gets the chemical names from the EntityList and normalizes the names. The pretrained model is trained with the normalized chemical names with the default hyperparameters.

In[]:=

chemicalNames= EntityValue[EntityList["Chemical"],"Name"];chemicalNames = Select[chemicalNames,StringMatchQ[#,CharacterRange["A","z"]..]&];normalizedChemicalNames = normalizeText@chemicalNames;

In[]:=

chemicalRNN = Import["/Users/sumansigdel/ChemicalRNN.wlnet"];Chemicalnet=NetReplacePart[NetExtract[chemicalRNN,"predict"],{"Input"NetEncoder[{"Characters",{vocabulary,EndOfString},"TargetLength"1}],"Output"NetDecoder[{"Class",Append[vocabulary,""]}]}];randomChemical[]:=With[{obj=NetStateObject[Chemicalnet]},StringJoin@NestWhileList[obj[Last[#],"RandomSample"]&,Sequence[{"",""},#=!={""}&,1,100]]];newChemicals=Sort@Complement[Table[randomChemical[],5000], normalizedChemicalNames];

Here are some chemical names that were generated by the RNN model.

In[]:=

RandomChoice[newChemicals,10]

Out[]=

{dopaquinox,lecalein,esopiulfon,methiocarbazide,bitosnan,mephoxybenzone,hexyldimethyloctylsilane,spiropentylbenzene,damuscinol,tetrachlorocyclodecane}

The performance of the RNN model is now calculated using the performance metric of euclidean distance between the n-grams.

ChemicalNamesDistancesRNN=Table[findEuclideanDistance[computeNGrams[newChemicals,n],computeNGrams[normalizedChemicalNames,n]],{n,1,5}]

Out[]=

{0.0129824,0.0123536,0.0120765,0.0122143,0.0126008}

In[]:=

BarChart[ChemicalNamesDistancesRNN,ChartLabels{"1 Gram","2 Gram","3 Gram","4 Gram","5 Gram"},ChartLegends{"RNN"},PlotLabel"Euclidean Distance between n-gram distribution for Chemical Names",ChartStyle{RGBColor["#a6cee3"]}]

Out[]=

RNN

In the above bar chart, we see that the euclidean distance for all the 1-5 n-grams are quite close to the actual dataset. In addition, the example that were generated from the RNN are also plausible examples.

2. Company Names

The same RNN model will now be trained with company names taken from Kaggle. The dataset contains over 7 million names and for the training we will only take names of companies that have string length of 6 or less. The following are some company names from the dataset

In[]:=

Take[normalizedShortCompaniesList,10]

Out[]=

{ibm,ey,att,pwc,citi,amazon,apple,oracle,nokia,hsbc}

normalizedShortCompaniesList=normalizeText@Select[Flatten@dataset,StringLength[#]≤6&];Take[normalizedShortCompaniesList,10]

Out[]=

{ibm,us army,ey,walmart,att,pwc,infosys,deloitte,citi,us navy}

Training the pretrained character level RNN on the company names dataset.

In[]:=

CompanyNamesnet=NetReplacePart[net,"Input"NetEncoder[{"Characters",{vocabulary,{StartOfString,EndOfString}97}}]]

CompanyNamesresults=NetTrain[CompanyNamesnet,<|"Input"normalizedShortCompaniesList|>,All,LossFunction"Loss",MaxTrainingRounds100]

Out[]=

NetGraph



uniniti

aliz

Input port:	string
Loss port:	real



Upon running the RNN model, the following examples were produced and the euclidean distance is calculated as per the performance metric.

In[]:=

generatedCompany=Sort@Complement[Table[randomGeneratedCompany[],1000],normalizedShortCompaniesList];Take[generatedCompany,10]

Out[]=

{aamp,aasu,aceic,acmas,acolux,actain,acws,adayi,addpowar,adio}

CompanyNamesDistancesRNN=Table[findEuclideanDistance[computeNGrams[generatedCompany,n],computeNGrams[SeedRandom[1234];RandomChoice[normalizedShortCompaniesList,1000],n]],{n,1,5}]

Out[]=

{0.0249101,0.0220684,0.0220686,0.0239113,0.027024}

In[]:=

BarChart[CompanyNamesDistancesRNN,ChartLabels{"1 Gram","2 Gram","3 Gram","4 Gram","5 Gram"},ChartLegends{"RNN"},PlotLabel"Euclidean Distance between n-gram distribution for Company Names",ChartStyle{RGBColor["#a6cee3"]}]

Out[]=

RNN

3. GANs for text generation

Generative Adversarial Networks or GANs are a deep learning architecture for training generative models in which two models (Generator and Discriminator) train in an adversarial zero sum game. After training
the generator is able to produce plausible example that are almost indistinguishable from the training set data. Recent improvements in GANs have significantly improved data augmentation in machine learning tasks that deal with images and in this section of the post some changes to a GAN architecture will be made in order for text generation. Similar to GANs used for images, the following models make use of Convolutional Blocks comprised of batch normalization, a Leaky ReLU non-linearity with an alpha of 0.2 and a dropout layer. I will begin by introducing the architecture for Discriminator and Generator and I will then train the composite GAN model on the same chemical names and company names and use the performance metric to get results for comparison.

Discriminator Model

The discriminator model is a binary classification model which simply differentiates if the data fed to the model is real (from the training data) or fake (from the generator). Initially we take the max values from the provided matrix, taking only the max values has no effect on the real samples matrix, however, it helps remove noise from the generator’s output matrix. Similar to GANs used for images, the following discriminator model makes use of Convolutional Blocks comprised of batch normalization, a Leaky ReLU non-linearity with an alpha of 0.2 and a dropout layer. The output layer is a LogisticSigmoid which gives us the probability of a text being real or fake.

In[]:=

discriminator=NetChain[<|"keep max only"NetGraph[{AggregationLayer[Max,-1],ThreadingLayer[If[#1≥#2-1.*^-7,#1,0]&,-1]},{{NetPort["Input"],1}2}],Sequence@@Table["conv."<>ToString[i]convolutionBlock[$numhiddens],{i,$depth}],"aggregate"AggregationLayer[Mean,1],"dropout"DropoutLayer[],"classify"LinearLayer["Real","Weights"0,"Biases"None],If[$jensen,"logit"LogisticSigmoid,Nothing]|>,"Input"{"Varying",Length[characters2]}]

Out[]=

NetChain



uniniti

aliz

Input port:	matrix (size: n 1 ×28)
Output port:	real



Generator Model

The generator model is used to generate plausible examples from a vector that is randomly drawn from a gaussian distribution. During the training, the generator assigns meaning to the vector and outputs examples similar to the training set . The generator is dependent on discriminator for its updates; better performance of discriminator results in more updates to the generator and vice versa . The generator model has several hyperparameters like the latent dimension, non-linearity and normalization which will be used for fine-tuning the model for better performance. The last layer of this model is a softmax layer which gives us the probability of each character occurring and this can be used in the decoder to turn probabilities into text.

In[]:=

generator=NetChain[<|If[$generatorTerminalTokensQ,(*Append/PrependEOS/SOSlatentvectors*)"add eos/sos latent"NetGraph[{ArrayLayer[],AppendLayer[],ArrayLayer[],PrependLayer[]},{{NetPort["Input"],1}2,{2,3}4}],Nothing],(*Coredeepnet*)Sequence@@Table["conv."<>ToString[i]convolutionBlock[$numhiddens],{i,$depth}],If[$generatorTerminalTokensQ,(*RemoveEOS/SOShighlevelfeatures*)"remove eos/sos prediction"NetChain[{SequenceRestLayer[],SequenceMostLayer[]}],Nothing],(*Classifier(ofcharacters)*)"classify"NetMapOperator@LinearLayer[Length[characters](*,"Weights"0*)],"squash"SoftmaxLayer[],If[$discriminatorTerminalTokensQ,"add eos/sos onehot proba"NetGraph[{(*CatenatezeroprobaforEOS/SOSinsidethegeneratedtext*)PaddingLayer[{{0,0},{0,2}}],(*Append/Prependprobaof1forEOS/SOSattheend/beginningofthegeneratedtext(tobeinaccordancewiththediscriminator)*)ArrayLayer["Array"UnitVector[Length[characters2],Length[characters2]-1],LearningRateMultipliersNone],PrependLayer[],ArrayLayer["Array"UnitVector[Length[characters2],Length[characters2]],LearningRateMultipliersNone],AppendLayer[]},{{1,2}3,{3,4}5}],Nothing]|>,"Input"{"n",$numlatent},"Output"With[{netpostproc=NetDecoder[netpreproc]},(*Capitalizethedecoded(lower-case)text*)NetDecoder[{"Function",Function[StringReplace[netpostproc[#],WordBoundary~~c:WordCharacterToUpperCase[c]]]}]]]

Out[]=

NetChain



uniniti

aliz

	Input	matrix (size: n ×16)
add eos/sos latent	NetGraph (4 nodes)	matrix (size: n 1 ×16)
conv.1	NetChain (4 nodes)	matrix (size: n 2 ×128)
conv.2	NetChain (4 nodes)	matrix (size: n 3 ×128)
remove eos/sos prediction	NetChain (2 nodes)	matrix (size: n 4 ×128)
classify	NetMapOperator[LinearLayer]	matrix (size: n 4 ×26)
squash	SoftmaxLayer	matrix (size: n 4 ×26)
add eos/sos onehot proba	NetGraph (5 nodes)	matrix (size: n 5 ×28)
	Output	expression

conv.1:

NetChain

	Input	matrix (size: n ×16)
1	ConvolutionLayer	matrix (size: n ×128)
2	BatchNormalizationLayer	matrix (size: n ×128)
3	ElementwiseLayer	matrix (size: n ×128)
4	DropoutLayer	matrix (size: n ×128)
	Output	matrix (size: n ×128)



CompositeGANModel

Wolfram Language contains a NetGANOperator to make a composite GAN model that takes generator and discriminator.

In[]:=

gan=NetGANOperator[{generator,discriminator}]

Out[]=

NetGANOperator



uniniti

alized



Trainingthemodel

It was found that the model performs better when the discriminator is updated twice as much as the generator. This makes significant updates to the generator in every epoch and also reduces the training time. In the NetTrain a data generator function is supplied which contains “sample” generation and “latent” vector generation.

Model Selection
GANs are very unstable during training as there are two networks that are dependent on each other for improvements in their performance. While several methods to improve the stability were implemented in the GAN architecture, they still suffer from non-convergence. Due to their unstable nature, an early stopping method fails to retrieve the best performing GAN model. In order to solve this, we will save a checkpoint of the model in every round along with the n-gram performance metric to select the best performing model.

dataGenerator={Function[<|"Sample"sampleGeneration[#BatchSize],"Latent"latentGeneration[#BatchSize]|>],"RoundLength"Length[normalizedNames]};

NetTrain[gan,dataGenerator,TargetDevice"GPU",BatchSize$batchsize,TrainingUpdateSchedule{"Discriminator","Discriminator","Generator"},MaxTrainingRounds100000,TrainingProgressFunction{{Function@Block[{generator,ngramDistance},generator=NetExtract[#Net,"Generator"];ngramDistance=DistancesofNgrams[generator,normalizedNames];Echo@ngramDistance;],"Interval"Quantity[10,"Rounds"]},{wssTrainingProgressFunction,"Interval"Quantity[10,"Rounds"]}},TimeGoaltimeGoal];

1. Chemical Names
The same dataset of chemical names was used to train the following GAN.

In[]:=

chemicalGAN=Import["/Users/sumansigdel/ChemicalGAN.wlnet"]

Out[]=

NetGANOperator



Sample:	matrix (size: n 1 ×28)
Latent:	matrix (size: n ×16)
LossReal:	real
LossFake:	real
GeneratedFake:	expression



We will now extract the generator from the GAN model and feed the latent random given by the latent generation function.

In[]:=

latentGeneration[batchSize_]:=Table[Block[{len=Max[3,RandomChoice[Values[counts]Keys[counts]]]},NumericArray[#,"Real32"]&@Clip[RandomVariate[NormalDistribution[],{len,16}],{-1,1}]],batchSize];

chemicalGenerator=NetExtract[chemicalGAN,"Generator"];

Here are 10 chemical names generated by the GAN.

In[]:=

chemicalGenerator@latentGeneration[10]

Out[]=

{Cephouromonazine,Cidenazine,Deropylltertine,Tramltne,Dinoamoldoxol,Metrexol,Flophabetrone,Poribeazene,Sulothlariyline,Macerminezone}

We now use the performance metric with the chemical names and plot a bar chart.

In[]:=

chemicalDistanceGAN=DistancesofNgrams[chemicalGenerator,normalizedChemicalNames]

Out[]=

{0.024628,0.0320187,0.0304281,0.0268123,0.0225618}

In[]:=

BarChart[chemicalGANDistance,ChartLegends{"GAN"},ChartLabels{"1 Gram","2 Gram","3 Gram","4 Gram","5 Gram"},PlotLabel"Euclidean Distance between n-gram distribution for Chemical Names",ChartStyle{RGBColor["#1f78b4"]}]

Out[]=

GAN

2.CompanyNames

Similarly, we will now train another GAN model on company names of String Length less than or equal to 6. Upon evaluation of the n-gram metric during training in every 10 rounds there was not a significant change to the euclidean distances. A few tweaks were made to the GAN model. The latent dimension was reduced to 10 and the first convolutional layer of the generator had only 64 filters instead of 128.

In[]:=

companyGAN=Import["/Users/sumansigdel/CompanyGAN3rd.wlnet"]

Out[]=

NetGANOperator





In[]:=

latentGeneration[batchSize_]:=Table[Block[{len=Max[3,RandomChoice[Values[counts]Keys[counts]]]},NumericArray[#,"Real32"]&@Clip[RandomVariate[NormalDistribution[],{len,10}],{-1,1}]],batchSize];

In[]:=

companyGenerator=NetExtract[companyGAN,"Generator"];

companyGenerator@latentGeneration[10]

Out[]=

{Pipsf,Sins,Gsacs,Pegvg,Amgia,Rapen,Rvdi,Rfd,Meme,Abm}

companyGANDistance=DistancesofNgrams[companyGenerator,normalizedShortCompaniesList]

Out[]=

{0.0239126,0.0439251,0.0315068,0.0235774,0.0228289}

In[]:=

BarChart[companyGANDistance,ChartLegends{"GAN"},ChartLabels{"1 Gram","2 Gram","3 Gram","4 Gram","5 Gram"},ChartStyle{RGBColor["#1f78b4"]},PlotLabel"Euclidean Distance between n-gram distribution for Company Names"]

Out[]=

GAN

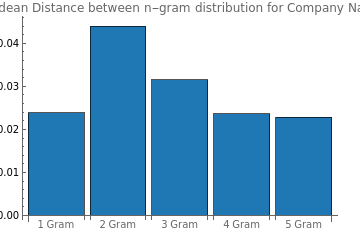Comparison and Conclusion

The computed euclidean distance between the n-gram distributions for both the RNN and GAN model will help us make a better comparison between two model.

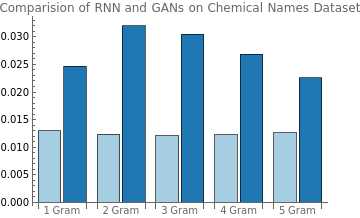
1.RNNvsGAN(ChemicalNames)

In[]:=

BarChart[Transpose@{ChemicalNamesDistancesRNN,chemicalDistanceGAN},ChartLayout->"Grouped",ChartStyle{RGBColor["#a6cee3"],RGBColor["#1f78b4"]},ChartLegends{"RNN","GAN"},ChartLabels{{"1 Gram","2 Gram","3 Gram","4 Gram","5 Gram"},None},PlotLabel"Comparision of RNN and GANs on Chemical Names Dataset"]

Out[]=

	RNN
	GAN

2.RNNvsGAN(CompanyNames)

In[]:=

BarChart[Transpose@{CompanyNamesDistancesRNN,companyGANDistance},ChartLayout->"Grouped",ChartStyle{RGBColor["#a6cee3"],RGBColor["#1f78b4"]},ChartLegends{"RNN","GAN"},ChartLabels{{"1 Gram","2 Gram","3 Gram","4 Gram","5 Gram"},None}]

Out[]=

	RNN
	GAN

From the above comparison, we can see that the GAN model’s for chemical names wasn’t too significant, however, for the company names dataset GAN’s performance was comparable and if not better (for 1,4 and 5 grams). This could be because the chemical names (8+ characters) were longer compared to company names (6 or less characters). We believe that further fine tuning and some architectural changes can improve the overall performance of the GAN model for both the datasets. In addition, the “Wolfram English Character-Level Language Model V1” was pretrained with training set consisting of 1.5 GB of text from old novels and news articles, which might have made it easier for the RNN model to learn the text features quickly while the GAN was trained from scratch and for fewer rounds. All in all, the GAN model’s performance even with shorter training on the same datasets is impressive.

Complete project work

Text Interpolation

In[]:=

chemicalGenerator=NetExtract[chemicalGAN,"Generator"];

In[]:=

p1=latentGeneration[100];

In[]:=

p2=latentGeneration[100];

In[]:=

p1Norm=Normal@p1;p2Norm=Normal@p2;

interpolate[p1_,p2_]:=Table[(1.0-n)*p1+n*p2,{n,0,1,0.1}];

In[]:=

interpolate[#[[1]],#[[2]]]&/@Transpose@{p1Norm,p2Norm};

In[]:=

NumericArray[#,"Real32"]&/@interpolate[#[[1]],#[[2]]]&/@Transpose@{p1Norm,p2Norm};

In[]:=

m=chemicalGenerator[#]&/@%;

In[]:=

m=Join[#,Reverse[#]]&/@m;

In[]:=

chemicalGenerator@p1

Out[]=

{Methylpaol,Closepreie}

In[]:=

chemicalGenerator@p2

Out[]=

{Mietoetayl,Amlonatine}

In[]:=

gif=ListAnimate[Multicolumn[#,FrameAll]&/@Transpose@m]

Out[]=

Keywords

◼

Deep Learning

◼

Generative Adversarial Networks

◼

Text Generation

Acknowledgment

Mentor: Tuseeta Banerjee

Thanks to Jerome Louradaur for guidance and initial GAN code.

References

◼

Cite this as: Suman Sigdel, "[WSS20] Text Generation Using GANs" from the Notebook Archive (2020), https://notebookarchive.org/2020-07-6hfo8lo

Text Generation using GANs

Wolfram Community Post (material for blog post)

1. Performance Metric

2. RNN Model​​The RNN model that will be used for comparison is the pretrained Wolfram English Character-Level Language Model V1.The following is the architecture of this model :

1. Chemical Names

2. Company Names

3. GANs for text generation

Complete project work

Text Interpolation

Keywords

Acknowledgment

References

2. RNN Model

The RNN model that will be used for comparison is the pretrained
Wolfram English Character-Level Language Model V1.
The following is the architecture of this model :