Iterative Solution of Highly Nonlinear Boundary Value Problems
Author
Frank Kampas
Title
Iterative Solution of Highly Nonlinear Boundary Value Problems
Description
Nonlinear boundary value differential equations are usually solved with the 'shooting method'. In this technique, the initial conditions are adjusted until the boundary conditions at the other boundary are satisfied. In situations in which the shooting method fails, the iterative 'relaxation' method can be used. Initial guesses at the solution are improved repeatedly. The relaxation method can be implemented using 'quasi-linearization'. The differential equation is linearized about the guessed solution and the linearized boundary value problem is solved. This technique can be implemented in a very straight-forward fashion in Mathematica because the numerical solutions to differential equations are interpolating functions. Quasi-linearization is first demonstrated with a single differential equation and then with the 5 coupled differential equations which describe a p-n junction.This submission is an update to a previous submission (see URL below). I have updated the code, improved the ...
Category
Educational Materials
Keywords
URL
http://www.notebookarchive.org/2018-10-10r4f9v/
DOI
https://notebookarchive.org/2018-10-10r4f9v
Date Added
2018-10-02
Date Last Modified
2018-10-02
File Size
366.64 kilobytes
Supplements
Rights
Redistribution rights reserved
 This notebook has not been updated since 2013.
This notebook has not been updated since 2013. 
Iterative Solution of Highly Nonlinear Boundary Value Problems
Iterative Solution of Highly Nonlinear Boundary Value Problems
Frank J. Kampas
Physicist at Large Consulting
Physicist at Large Consulting
Frank @ Physicistatlarge.com
Introduction
Nonlinear boundary value differential equations are usually solved with the "shooting method". In this technique, the initial conditions are adjusted until the boundary conditions at the other boundary are satisified. In situations in which the shooting method fails, the iterative "relaxation" method can be used. Initial guesses at the solution are improved repeatedly. The relaxation method can be implement using "quasi-linearization". The differential equation is linearized about the guessed solution and the linearized boundary value problem is solved. This technique can be implemented in a very straight-forward fashion in Mathematica because the numerical solutions to differential equations are interpolating functions.
Quasi-linearization is first demonstrated with a single differential equation and then with the 5 coupled differential equations which describe a p-n junction.
Quasi-linearization is first demonstrated with a single differential equation and then with the 5 coupled differential equations which describe a p-n junction.
Troesch's Equation
The shooting method is problematic for Troesch's equation, y'' = 5 Sinh(5 y), y(0)=0, y(1) =1, as the solution has a singularity at approximately at x = 1.03, unless the initial estimate of the value of the derivative at x = 0 is very good. In the following calculation, shootsoln is the parametric solution to Troesch's equation, as a function of d, which is equal to y'(0).
shootsoln=ParametricNDSolve[{y''[x]-5Sinh[5y[x]]==0,y[0]==0,y'[0]==d},y,{x,0,1},{d}]〚1〛
yParametricFunction[<>]
FindRoot is used to find the value of d for which the solution satisfies the boundry condition at x = 1. The error messages from FindRoot come from values of d which result in solutions which are singular in the range x = 0 to x = 1. These messages show the problems associated with the shooting method for this type of boundary value problem.
soln=y[d]/.FindRoot[(y[d][1]/.shootsoln)1,{d,0,.01}]〚1〛/.shootsoln
ParametricNDSolve::ndsz:At x$334 == 0.957898, step size is effectively zero; singularity or stiff system suspected.
InterpolatingFunction::dmval:Input value {1} lies outside the range of data in the interpolating function. Extrapolation will be used.
ParametricNDSolve::ndsz:At x$334 == 0.965973, step size is effectively zero; singularity or stiff system suspected.
InterpolatingFunction::dmval:Input value {1} lies outside the range of data in the interpolating function. Extrapolation will be used.
ParametricNDSolve::ndsz:At x$334 == 0.975065, step size is effectively zero; singularity or stiff system suspected.
General::stop:Further output of ParametricNDSolvendsz will be suppressed during this calculation.
InterpolatingFunction::dmval:Input value {1} lies outside the range of data in the interpolating function. Extrapolation will be used.
General::stop:Further output of InterpolatingFunctiondmval will be suppressed during this calculation.
InterpolatingFunction[{{0.,1.}},<>]
Plot[soln[x],{x,0,1},PlotRangeAll,FrameTrue]

Note the correct value of y'[0].
soln'[0]
0.0457504
When the shooting method fails, quasi-linearization can be employed. The non-linear differential equation is linearized about a function and the linearized differential equation is solved using the shooting method. This is repeated until the solution has sufficient accuracy. The process can be thought of as an application of Newton’s method to functions. (Zwillinger, p. 524)
The following function linearizes the left-hand side of the differential equation by implementing a Taylor series to first order. The functions and the derivatives in the expression are input as vars, and the base functions and derivatives about which expr is linearized are input as noms.
lin[expr_,vars_,noms_]:=Module[{r=Thread[vars->noms]},(expr/.r)+(vars-noms).((D[expr,#]&/@vars)/.r)]//FullSimplify
Troesch=y''[x]-5Sinh[5y[x]];
linTroesch[ys_]=lin[Troesch,{y[x],y''[x]},{ys[x],ys''[x]}]
-5Sinh[5ys[x]]+25Cosh[5ys[x]](-y[x]+ys[x])+[x]
′′
y
For quasilinearization, shootsoln is rewritten as a function of the starting solution.
Clear[shootsoln]
shootsoln[ys_]:=ParametricNDSolve[{linTroesch[ys]==0,y[0]==0,y'[0]==d},y,{x,0,1},{d}]〚1〛
The function iter improves the solution using the shooting method to solve the linearized differential equation. Note that its input and output are anonymous functions. This allows the evaluation of derivatives.
iter[ys_]:=Module[{s=shootsoln[ys],dd},dd=d/.FindRoot[Evaluate[y[d][1]/.s]1,{d,ys'[0],ys'[0]+0.001}];y[dd]/.s]
The function #&, which satisfies the initial conditions, is used as the starting function.
l=NestList[iter,#&,7];
The following plot shows the convergence
Plot[Evaluate[Through[l[x]]],{x,0,1},FrameTrue,PlotLegendsRange[8]]
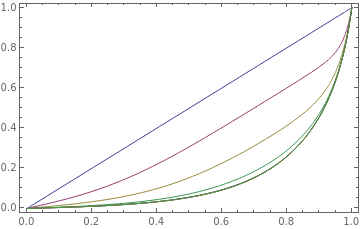 |
|
All of the solutions satisfy the boundary conditions.
Through[l[0]]
{0,0.,0.,0.,0.,0.,0.,0.}
Through[l[1]]
{1,1.,1.,1.,1.,1.,1.,1.}
The value of y'(0) converges to the value found earlier by the shooting method
Table[l[[i]]'[0],{i,8}]
{1,0.366249,0.14271,0.0611267,0.0461923,0.0457508,0.0457504,0.0457504}
P-N Junction Transport Equations
Modeling of p-n junctions is typically performed by dividing the junction into neutral regions near the contacts and a depletion region in the center. The transition between these regions is neglected. (See Sze, chapter 3). In this section, those approximations are not made.
The equations describing the electron and hole transport in a p-n junction cannot be solved by the shooting method, but can be solved with quasi-linearization, as the dependence of the carrier densities on the quasi-Fermi levels is exponential.
The two following equations give the electron density n as a function of potential v and the electron quasi-Fermi level ϕn and the hole density p as a function of the potential and the hole quasi-Fermi level ϕp. ni is the intrinsic carrier density, β = where k is Boltzmann's constant and T is the absolute temperature.
1
kT
n[v_,ϕn_]=ni*Exp[β(v-ϕn)];p[v_,ϕp_]=ni*Exp[β(ϕp-v)];
The total charge density ρ[x] is equal to the dopant charge density dp[x] + the electron and hole charge densities.
ρ[x_]=dp[x]-n[v[x],ϕn[x]]+p[v[x],ϕp[x]];
The following 5 terms are equal to 0 when the differential equations are satisfied. jn and jp are the electron and hole current densities, respectively. The first two equations give the relationship between the current densities and the quasi-Fermi levels. The third equation is Poisson's equation. The fourth and fifth equations reflect the fact that the current densities are independent of x in steady-state.
eq1=ϕn'[x]+jn[x]/(qμnn[v[x],ϕn[x]]);eq2=ϕp'[x]+jp[x]/(qμpp[v[x],ϕp[x]]);eq3=v''[x]+(q/ϵ)ρ[x];eq4=jn'[x];eq5=jp'[x];
eqs is a list of the five equation left-hand sides.
eqs={eq1,eq2,eq3,eq4,eq5};
The linearized differential equations are functions of the starting functions, whose names end in s.
delin[vs_,ϕns_,ϕps_,jns_,jps_]=lin[eqs,{v[x],v'[x],v''[x],ϕn[x],ϕn'[x],ϕp[x],ϕp'[x],jn[x],jp[x]},{vs[x],vs'[x],vs''[x],ϕns[x],ϕns'[x],ϕps[x],ϕps'[x],jns[x],jps[x]}]
(jn[x]+βjns[x](-v[x]+vs[x]+ϕn[x]-ϕns[x]))+niqμn[x](niqμn),(jp[x]+βjps[x](v[x]-vs[x]-ϕp[x]+ϕps[x]))+niqμp[x](niqμp),(1/ϵ)(-+)niq+qdp[x]+niqβ(-v[x]+vs[x]+ϕn[x]-ϕns[x])+(-v[x]+vs[x]+ϕp[x]-ϕps[x])+ϵ[x],[x],[x]
β(-vs[x]+ϕns[x])
′
ϕn
β(vs[x]-ϕps[x])
′
ϕp
β(vs[x]-ϕns[x])
β(-vs[x]+ϕps[x])
β(vs[x]-ϕns[x])
β(-vs[x]+ϕps[x])
′′
v
′
jn
′
jp
The following are the initial conditions for the linearized equations. e0 is the electric field as x = 0. The quasi-Fermi levels are equal to each other and to ϕ0 at the left boundary.
ics={v[0]==v0,ϕn[0]==ϕ0,ϕp[0]==ϕ0,-v'[0]==e0,jn[0]==jn0,jp[0]==jp0};
The following are values of various constants
q=1.6;(*thechargeonanelectroninCoulombs*)k=1.38;(*Boltzmann'sconstant*)t=300;(*thetemperatureindegreesKelvin*)β=q/(kt);μn=1500;(*theelectronmobility*)μp=450;(*theholemobility*)ni=1.45;(*theintrinsiccarrierdensity*)ϵ=11.9*8.85;(*thepermitivityofsilicon*)w=;(*thetotalthicknessofthejunction*)
-19
10
-23
10
10
10
-14
10
-4
10
For an “abrupt” junction, the charge density from the dopants is -dop for and dop for <x<w. Therefore the junction is a p-n junction since the negatively charged acceptors are between 0 and and the positively charged donors are between and w.
0<x<
w
2
w
2
w
2
w
2
dop=;(*thedopantconcentration*)
15
10
dp[x_]=dop*Sign[x-w/2];(*thedopantprofile*)
Plot[dp[x],{x,0,w},FrameTrue,FrameLabel{"x","dopant charge density"},ExclusionsNone,PlotRangeAll]

The electric potentials at each end of the junction are given by
v0=0.0;(*thepotentialattheleftboundary*)v1=0.45;(*thepotentialattherightboundary*)
The built-in potential can be approximated from the concentration of dopants. The fact that the potential difference across the junction is less than the built-in potential indicates that the junction is forward biased.
vbi=Log
-1
β
2
dop
2
ni
0.576565
At the boundaries, the quasi-Fermi levels are equal and the total charge density dp - n + p is 0. This enables calculation of the values of the quasi-Fermi levels at the boundaries. FindRoot has some difficulties due to the exponential dependence of the charge density on the quasi-Fermi levels.
ϕ0=ϕ0/.FindRoot[dp[0]-n[v0,ϕ0]+p[v0,ϕ0]==0,{ϕ0,.3}]〚1〛
FindRoot::lstol:The line search decreased the step size to within tolerance specified by AccuracyGoal and PrecisionGoal but was unable to find a sufficient decrease in the merit function. You may need more than MachinePrecision digits of working precision to meet these tolerances.
0.288283
ϕ1=ϕ1/.FindRoot[dp[1]-n[v1,ϕ1]+p[v1,ϕ1]==0,{ϕ1,.3}]〚1〛
FindRoot::lstol:The line search decreased the step size to within tolerance specified by AccuracyGoal and PrecisionGoal but was unable to find a sufficient decrease in the merit function. You may need more than MachinePrecision digits of working precision to meet these tolerances.
0.161717
The following function linsoln gives the solution to the linearized equation as a function of the starting functions vs, ϕns, ϕps, jns and jps.
linsoln[vs_,ϕns_,ϕps_,jns_,jps_]:= ParametricNDSolve[ Thread[Simplify[delin[vs,ϕns,ϕps,jns,jps]==0]]~Join~ics,{v,ϕn,ϕp,jn,jp},{x,0,w},{e0,jn0,jp0}]
The function iter calculates improved functions for the potential, the electron and hole quasi-Fermi levels, and the electron and hole current densities, using linsoln. The starting values for the required initial conditions are calculated from the input functions.
iter[{vs_,ϕns_,ϕps_,jns_,jps_}]:=Module[{s=linsoln[vs,ϕns,ϕps,jns,jps],vsi=vs'[0],jni=jns[0],jpi=jps[0],sln},sln=FindRoot[{(v[e0,jn0,jp0][w]/.s)v1,(ϕn[e0,jn0,jp0][w]/.s)ϕ1,(ϕp[e0,jn0,jp0][w]/.s)ϕ1},{{e0,-.95vsi,-1.05vsi},{jn0,.95jni,1.05jni},{jp0,.95jpi,1.05jpi}}];({v[e0,jn0,jp0],ϕn[e0,jn0,jp0],ϕp[e0,jn0,jp0],jn[e0,jn0,jp0],jp[e0,jn0,jp0]}/.sln)/.s]
The initial potential and quasi-Fermi level functions are assumed to be linear. The initial current density functions are assumed to be constant.
i0={(v0+((v1-v0)/w)#)&,(ϕ0+((ϕ1-ϕ0)/w)#)&,(ϕ0+((ϕ1-ϕ0)/w)#)&,1.0&,1.0&};
-7
10
-7
10
The function iter is applied 7 times.
iterations=NestList[iter,i0,7];
The following plot shows the convergence of v[x] .
Plot[Evaluate[Table[iterations[[nn,1]][x],{nn,8}]],{x,0,w},Ticks->{{{5,"5. "},{,"1. "}},Automatic},FrameTrue,FrameLabel{"x","v(x)"},PlotLegendsRange[8]]
-5
10
-5
10
-4
10
-4
10
 |
|
The next plot shows the convergence of ϕn[x] and ϕp[x] .
Plot[Evaluate[Join[Table[iterations[[nn,2]][x],{nn,8}],Table[iterations[[nn,3]][x],{nn,8}]]],{x,0,w},PlotRange->{{0,w},{.16,.30}},Ticks->{{{5,"5. "},{,"1. "}},Automatic},FrameTrue,FrameLabel"x","ϕn(x), ϕp(x)",PlotLegendsJoin[Table["ϕn"<>ToString[i],{i,8}],Table["ϕp"<>ToString[i],{i,8}]]]
-5
10
-5
10
-4
10
-4
10
 |
|
This table shows the convergence of the the electron current density jn .
Table[iterations[[nn,4]][0],{nn,8}]
{1.×,1.60941×,7.99326×,0.0000185232,0.0000167179,0.0000167075,0.0000167075,0.0000167075}
-7
10
-6
10
-6
10
The convergence of jp.
Table[iterations[[nn,5]][0],{nn,8}]
{1.×,6.31618×,2.8084×,5.56008×,5.01743×,5.01217×,5.01217×,5.01217×}
-7
10
-7
10
-6
10
-6
10
-6
10
-6
10
-6
10
-6
10
The convergence of the electric field at 0, e0 .
-Table[iterations[[nn,1]]'[0],{nn,8}]
{-4500.,-1699.59,-2002.18,-2005.41,-2005.41,-2005.41,-2005.41,-2005.41}
The converged potential, electron quasi-Fermi level, hole quasi-Fermi level, electron current, and hole current are given by vf, ϕnf, ϕpf, jnf and jpf.
{vf,ϕnf,ϕpf,jnf,jpf}=iterations〚8〛;
The total charge density can be calculated from the second derivative of the potential, per Poisson's equation. Most of the junction is depleted of carriers.
Plot[((-ϵ)/q)vf''[x],{x,0,w},PlotRange->{-1.1,1.1},Ticks->{{{5,"5. "},{,"1. "}},Automatic},FrameTrue,FrameLabel{"x","ρ(x)"}]
15
10
15
10
-5
10
-5
10
-4
10
-4
10

The electron and holes densities can be calculated from the potential and the quasi-Fermi levels.
Plot[{n[vf[x],ϕnf[x]],p[vf[x],ϕpf[x]]},{x,0,w},PlotRange->All,Ticks->{{{5,"5. "},{,"1. "}},Automatic},FrameTrue,FrameLabel{"x","n(x), p(x)"},PlotLegends{"n(x)","p(x)"}]
-5
10
-5
10
-4
10
-4
10
 |
|
A junction that is not abrupt might have a doping profile such as
dp[x_]=dop*Erf[(5(x-w/2))/w];
Plot[dp[x],{x,0,w},FrameTrue,FrameLabel{"x","dopant charge density"}]

Recalculating with this new dopant profile modifies the results. The total charge density result for this dopant profile is shown as an example.
iterations=NestList[iter,i0,7];
{vf,ϕnf,ϕpf,jnf,jpf}=iterations〚8〛;
Plot[((-ϵ)/q)vf''[x],{x,0,w},PlotRange->{-1.1,1.1},Ticks->{{{5,"5. "},{,"1. "}},Automatic},FrameTrue,FrameLabel{"x","ρ(x)"}]
15
10
15
10
-5
10
-5
10
-4
10
-4
10

Conclusion
Complex coupled nonlinear boundary value differential equations can be solved in Mathematica using quasi-linearization by taking advantage of Mathematica's unique use of interpolating functions for the numerical solution of differential equations.
References
Zwillinger, Daniel, “Handbook of Differential Equations”, 3rd edition, Academic Press, 1998
Sze, S.M., “Semiconductor Devices, Physics and Technology”, John Wiley & Sons, 1985
Sze, S.M., “Semiconductor Devices, Physics and Technology”, John Wiley & Sons, 1985
Cite this as: Frank Kampas, "Iterative Solution of Highly Nonlinear Boundary Value Problems" from the Notebook Archive (2013), https://notebookarchive.org/2018-10-10r4f9v
Download
