25 Point Spikey

by Ed Pegg Jr, Michael Trott, and Mark Peterson

redone for 2015 by Ed Pegg Jr

Original explanation (evaluate all this)

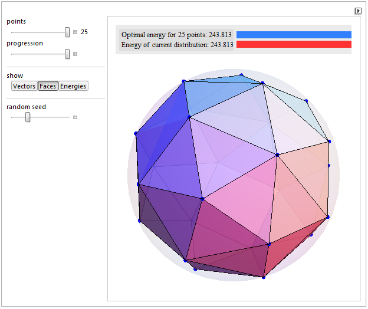
For the 25th anniversary, we wanted a 25 point Spikey of some sort. We decided to use the solution for the 25 point Thomson problem, which minimizes the energy of 25 point charges on a sphere. For that, we can look at Visualizing the Thomson Problem, a Demonstration by Mark Peterson.

In[]:=

In the Demonstration, solutions up to 25 points are illustrated. Classic minimization methods are used to find the solution.

In[]:=

point[j_]:={Cos[φ[j]]Sin[ϑ[j]],Sin[φ[j]]Sin[ϑ[j]],Cos[ϑ[j]]};totalEnergy=Sum[1/Sqrt[(point[j]-point[k]).(point[j]-point[k])],{j,25},{k,j+1,25}];SeedRandom[123];fm=FindMinimum[Evaluate[totalEnergy],Evaluate[Join[Table[{φ[j],RandomReal[{0,2Pi}]},{j,25}],Table[{ϑ[j],RandomReal[{0,Pi}]},{j,25}]]],MaxIterations10000,PrecisionGoal6,WorkingPrecision20];pts=First[Table[point[j],{j,25}]/.Rest[fm]];

That gives the 25 points of a solution. We need the polygons for the corresponding polyhedron. The triangles will be relatively “far” from the origin, so we can search for those.

In[]:=

distancetriangleorigin[pt1_,pt2_,pt3_]:=Abs[Det[{pt1,pt2,pt3}]/Sqrt[Sum[Det[ReplacePart[{pt1,pt2,pt3},{{1,c},{2,c},{3,c}}1]]^2,{c,1,3}]]];max=25;polygons={};Do[If[d>e>i&&distancetriangleorigin[pts[[d]],pts[[e]],pts[[i]]]>1-3.4/max,polygons=Append[polygons,{d,e,i}]],{d,3,max},{e,2,max},{i,1,max}];

The polygons are now known. We’re going to be 3D printing this, so triangle orientation matters. In a 3D printed object, all the outer faces need to have the same handedness, which we’ll represent with green and red. Taking a determinant can find the handedness. After that, a square in the solution leads to a set of overlapping triangles, so we number them to determine which polygons to drop.

In[]:=

poly2=If[Sign[Det[pts[[#]]]]1,#,Reverse[#]]&/@polygons;Graphics3D[{FaceForm[Green,Red],Polygon[pts[[#]]]&/@poly2,MapIndexed[Text[#2[[1]],Total[pts[[#1]]]/3]&,poly2]},BoxedFalse,SphericalRegionTrue,ViewAnglePi/10]

Out[]=

The 25-vertex polyhedron is printable once triangles 28 & 29 are removed. If any of the triangles in the above were red, their orientation would not be understood by the 3D printing process. From there, we hyperbolize the edges. If this wasn’t expensive 3D printing, we could stop there and print a solid hyperbolized polyhedron.

In[]:=

poly=Drop[poly2,{28,29}];hyperbolice[r_?VectorQ,α_]:=r(r.r)^αmp[n_]:=mp[n]=Mean[pts[[poly[[n]]]]];p1[n_]:=p1[n]=pts[[poly[[n,1]]]];p2[n_]:=p2[n]=pts[[poly[[n,2]]]];p3[n_]:=p3[n]=pts[[poly[[n,3]]]];

To save costs, we put a hole in each triangle. Since we have 46 triangles, we need to calculate 46×3 different surfaces. These surfaces are shrunk by .95 to get inner surfaces, then new triangles to connect everything up. If done correctly, everything will be green. Various steps with red triangles showing have been omitted.

Old Version (no need to evaluate)

Graphics3D[{FaceForm[Green,Red],EdgeForm[None],Table[With[{jj=Table[Evaluate[hyperbolice[mp[n]+s((1-t)(#1[n]-mp[n])+t(#2[n]-mp[n])),2.4]],{s,.6,1,.1},{t,0,1,.1}]&@@@{{p1,p2},{p2,p3},{p3,p1}}},With[{kk=.95jj,r1=Sequence[1,5],r2=Sequence[6,10]},{Function[{v,f},Polygon/@Table[f@{v[[g,a+#1,b+#2]],v[[g,a+#3,b+#4]],v[[g,a+#5,b+#6]]},{a,1,4},{b,##7}]&@@@{{0,0,1,0,0,1,r2},{1,0,1,1,0,1,r2},{0,0,1,1,0,1,r1},{0,0,1,0,1,1,r1}}]@@@{{jj,Identity},{kk,Reverse}},Polygon/@Table[Reverse[{jj[[g,1,b]],kk[[g,1,b]],kk[[g,1,b+1]],jj[[g,1,b+1]]}],{b,1,10}]}]],{g,1,3},{n,1,46}]},BoxedFalse,SphericalRegionTrue,ViewAnglePi/10,ImageSize{400,400}]

Now this can be exported as an STL object.

New Version (evaluate after evaluating first part)

WREL has started use the 25th Anniversary spikey as an award at their user conference. The original one we did was in metal but since they we have been told that they will print it but not polish it correctly because they are afraid it will harm other 3D prints in the machine, or the machine itself.

We asked them if it would be possible to get it printed if we sent them a file with the points already rounded (which is what happens when it is polished). They indicated they would need us to do that as well as increase the wall thickness in some areas to 1.5mm.

Areas in orange are too thin.

There are thus two problems caused by inner and outer spikes. The outer spikes are too sharp, and the inner spikes cause a lot of thin walls. Here’s some code for truncating these troublesome spikes.

With the new version, the sharp points are removed inside and out. The walls were made slightly thicker. Since the object will be polished, more subdivisions were used so that the figure would looks smoother out of the printer.

pts=Normal

List

;poly={{7,5,2},{8,6,1},{2,3,11},{11,7,2},{14,11,3},{14,13,11},{12,13,14},{15,14,3},{12,14,15},{5,7,16},{17,9,8},{4,10,18},{18,15,3},{7,11,19},{19,13,9},{11,13,19},{19,16,7},{9,17,19},{19,17,16},{4,5,20},{5,16,20},{16,17,20},{6,8,21},{8,9,21},{21,12,6},{9,13,21},{21,13,12},{22,8,1},{22,17,8},{22,20,17},{23,3,2},{2,5,23},{23,5,4},{23,18,3},{4,18,23},{1,6,24},{24,10,1},{6,12,24},{12,15,24},{24,18,10},{15,18,24},{1,10,25},{25,10,4},{4,20,25},{25,22,1},{20,22,25}};truncate[poly_,amount_]:=Module[{maxinmiddle,normal,sub1,sub2},maxinmiddle=Last[SortBy[Table[RotateRight[poly,n],{n,0,2}],Norm[#[[2]]]&]];normal=Nearest[pts,maxinmiddle[[2]]][[1]];sub1=a/.Quiet[Solve[{((amaxinmiddle[[1]]+(1-a)maxinmiddle[[2]])-(1-amount)maxinmiddle[[2]]).normal0,a>0}]][[1]];sub2=a/.Quiet[Solve[{((amaxinmiddle[[3]]+(1-a)maxinmiddle[[2]])-(1-amount)maxinmiddle[[2]]).normal0,a>0}]][[1]];{{maxinmiddle[[1]],(sub1maxinmiddle[[1]]+(1-sub1)maxinmiddle[[2]]),(sub2maxinmiddle[[3]]+(1-sub2)maxinmiddle[[2]]),maxinmiddle[[3]]},{(sub1maxinmiddle[[1]]+(1-sub1)maxinmiddle[[2]]),(1-amount)maxinmiddle[[2]],(sub2maxinmiddle[[3]]+(1-sub2)maxinmiddle[[2]])}}]hyperbolice[r_?VectorQ,α_]:=r(r.r)^αmp[n_]:=mp[n]=Mean[pts[[poly[[n]]]]];p1[n_]:=p1[n]=pts[[poly[[n,1]]]];p2[n_]:=p2[n]=pts[[poly[[n,2]]]];p3[n_]:=p3[n]=pts[[poly[[n,3]]]];thickness=.07777;(*Was.05*)truncationamount=.025;

The following takes several minutes.

polishedspikey=Graphics3D[{FaceForm[Green,Red],EdgeForm[None],If[Max[Norm/@#]1||Max[Norm/@#](1-thickness),Polygon[truncate[#,truncationamount]],Polygon[#]]&/@Flatten[If[Length[Dimensions[#[[1]]]]2,{#[[1]]},#[[1]]]&/@Flatten[Table[With[{jj=Table[Evaluate[hyperbolice[mp[n]+s((1-t)(#1[n]-mp[n])+t(#2[n]-mp[n])),2.4]],{s,.6,1,.1},{t,0,1,.02}]&@@@{{p1,p2},{p2,p3},{p3,p1}}},With[{kk=(1-thickness)jj,r1=Sequence[1,25],r2=Sequence[26,50]},{Function[{v,f},Polygon/@Table[f@{v[[g,a+#1,b+#2]],v[[g,a+#3,b+#4]],v[[g,a+#5,b+#6]]},{a,1,4},{b,##7}]&@@@{{0,0,1,0,0,1,r2},{1,0,1,1,0,1,r2},{0,0,1,1,0,1,r1},{0,0,1,0,1,1,r1}}]@@@{{jj,Identity},{kk,Reverse}},Polygon/@Table[Reverse[{jj[[g,1,b]],kk[[g,1,b]],kk[[g,1,b+1]],jj[[g,1,b+1]]}],{b,1,50}]}]],{g,1,3},{n,1,46}]],1]},BoxedFalse,SphericalRegionTrue,ViewAnglePi/10,ImageSize{600,600}]

It can then the exported. Your file path may vary.

Export["C:\\Users\\edp\\Desktop\\polishedspikey.stl",polishedspikey,"STL"]

C:\Users\edp\Desktop\polishedspikey.stl

Cite this as: Ed Pegg Jr., "25 Point Spikey" from the Notebook Archive (2018), https://notebookarchive.org/2018-12-3a4b0nu