Essays, Posts & Presentations

Stippling portrait of Margaret Heafield Hamilton

Silvia Hao

Author

Silvia Hao

Title

Stippling portrait of Margaret Heafield Hamilton

Description

Stylish portraits of Margaret Heafield Hamilton are generated with the technique of stippling drawing

A Wolfram Notebook on Stippling Drawing

Introduction

Stippling is a kind of drawing style using only points to mimic lines, edges, and grayscale. The entire drawing consists only of dots on a white background. The density of the points gives the impression of grayscale shading.

Typical stippling almost always uses one or two colors. Actually, one can create all sorts of textures and tones without introducing artifacts—one cannot achieve both with techniques like hatching or line drawing—just by varying the density and distribution of the dots. That makes stippling an excellent choice when archaeologists, geologists, and biologists are doing fieldwork and want to record things they find immediately. They don’t want to travel along with heavy painting gear; a single pen is good enough for stippling. Even in modern days, compared to photography, stippling still holds some advantages despite requiring a large amount of time. For example, the author can mark and emphasize any features he or she wants right on the drawing; thus, the technique is an important skill—one that is still being taught and researched today.

In the computer age, there is a special computer graphics domain called non-photorealistic rendering. Stippling is one of its basic artistic painting styles, and can be used as the foundation of many other synthetic styles, such as mosaic, stained glass, hatching, etc.

It is possible to generate a stippling drawing from any image programmatically. There are not only lots of papers on this topic, but also well-made applications. In this notebook we are going to demonstrate how to do it with the Wolfram Language.

The essential properties of a good stippling

When using points to approximate a grayscale, a random set of points with uniform distribution is usually not good enough. To illustrate, both images below try to use 2500 points to approach a uniform grayscale square, but the one on the right is a good stippling (or usually called well-spaced). The one on the left has too many unwanted small artifacts — clumps and voids that should not exist.

It can be seen that there are too many unwanted small artifacts in the former one -- clumps and voids that do not exist in the original image.

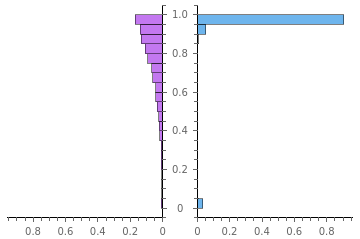
Moreover, for those who come from computing geometry background, checking the mesh qualities of the corresponding Delaunay meshes will give another intuitive impression that a good stippling tends to give a high quality mesh:

In[1]:=

Function[pts,PropertyValue[{DelaunayMesh[pts],2},MeshCellQuality]]/@

data cache

size:

42.0

→

11.5

rate:

0.274

type:

List

data cache

size:

41.9

→

11.3

rate:

0.269

type:

List

//PairedHistogram[Sequence@@#,Automatic,"Probability",ChartLegendsPlaced[{"random mesh","stippling mesh"},Below],ChartStyle{"Pastel",None,None}]&

Out[]=

random mesh

stippling mesh

Get started -- stippling of a uniform area

For an easy start we consider the stippling technique for a uniform area (i.e. an area with constant grayscale). There is a de facto standard method for it called centroidal Voronoi diagram (CVD) which is usually generated by the Lloyd’s algorithm.

Basically, the algorithm acts as the following relaxation steps:

Generate

random points inside the region of interest

Generate the Voronoi diagram of the

points

Find the centroid of each Voronoi cell

Use the

centroids as the resulting points

If satisfied, stop; otherwise, return to step 1

Here the key techniques are the Voronoi diagram generation and the centroid finding. The former one is a perfect match for the bounded version of the built-in function VoronoiMesh, while the latter one is exactly for MeshCellCentroid.

As a test, we generate 500 uniformly distributed random points in a square region

[-1,1]×[-1,1]

In[1]:=

initPts=RandomPoint[Rectangle[{-1,-1},{1,1}],500];

Its Voronoi diagram is:

In[2]:=

VoronoiMesh[initPts,{{-1,1},{-1,1}}]//Graphics[{GrayLevel[.6],Line[Identity@@@MeshPrimitives[#,1]],Red,AbsolutePointSize[2],Point[initPts]}]&

Out[]=

By animating the first 50 iterations of the algorithm, it can be seen clearly how the points distributed more and more evenly:

In[3]:=

Module[{initPts=initPts,res,allframes,vormeshGen=VoronoiMesh[#,{{-1,1},{-1,1}}]&},res=NestList[PropertyValue[{vormeshGen@#,2},MeshCellCentroid]&,initPts,50];refinedPts=Last@res;allframes=Graphics[{GrayLevel[.6],Line[Identity@@@MeshPrimitives[vormeshGen@#,1]],Red,AbsolutePointSize[2],Point[#]}]&/@res;ListAnimate[allframes〚1;;-1;;5〛]]

Out[]=

There are various ways to show the difference between the point distributions before and after the process.

For example we can use NearestNeighborGraph to illustrate their connectivity, which will highlight the unwanted voids in the former case:

In[4]:=

MapThread[Function[{pts,label},Graphics[Line[EdgeList[NearestNeighborGraph[pts,3]]/.UndirectedEdgeList],ImageSize300]//{Style[label,20,FontFamily"Constantia"],#}&],{{initPts,refinedPts},{"initial random points","CVD refined points"}}]//Grid[#,AlignmentLeft,FrameAll]&

Out[]=

We have seen the view angle from mesh quality. Another intuitive point of view comes from the discrete Fourier transform. To make the result clearer, a denser example (2,500 points per each) is used.

In[5]:=

Module{initPts,refinedPts},{initPts,refinedPts}=

data cache

size:

42.0

→

11.5

rate:

0.274

type:

List

data cache

size:

41.9

→

11.3

rate:

0.269

type:

List

;MapThreadFunction{pts,label},Graphics[{AbsolutePointSize[0],Point@pts}]//Rasterize[#,ImageSize{701,701}]&//Binarize//ColorNegate//Function[img,ImageMultiply[img,DiskMatrix[.4ImageDimensions[img],ImageDimensions[img]]//Image]]//ImageData//#-Mean[Flatten@#]&//Fourier//Abs//Rescale//RotateRight#,Floor

Dimensions[#]

&//Image[1.2-

(1-#)

,"Real",ImageSize300]&//{Style[label,20,FontFamily"Constantia"],#}&,{{initPts,refinedPts},{"initial random points","CVD refined points"}}//Grid[#,AlignmentLeft,FrameAll]&

Out[]=

Basically, the Fourier transform counts the significances of periodic structures with different periods. The ones with the largest periods (say, a structure repeating every 100 pixels) correspond to center-most positions, and the ones with the smallest periods (say, a structure repeating every 2 pixels) correspond to the furthest positions. The value at a position indicates the significance of the corresponding structure. In the above plots, the larger values are illustrated with whiter colors. The center white spots correspond to the sum of all the data, which is not of interest here. In the initial case, the significances of different periodic structures are almost the same; this indicates that it is a uniform random distribution (or so-called white noise). The refined case is more interesting. The large-scale periodic structures are all flattened out, illustrated as a black disk region around the center spot, which means the points distribute uniformly on the macro scale. Then there is a bright circle around the dark disk region. The circle shape indicates that the positions in that circle correspond to structures with nearly the same period but in different directions, which are the approximately equilateral triangles in the mesh with nearly the same size but random directions. The outer “rings” correspond to high-order structures, which should not appear in a perfect refined case. So it can be clearly seen that the refined points’ case effectively achieves both isotropism and low-stop filter. This is another facet of view to understand the term “well spaced.” Now I can say that the property is also related to the concept of the “blue color” of noise.

Advanced -- stippling of a non-uniform area

The Lloyd’s algorithm described above can not be directly adapted here without modification, as it always smooths out the distribution, results a uniform CVD. So how can we generalize it to non-uniform case?

Approach using the conformal mapping

Recall that we were looking for a Delaunay mesh with cells that resembles equilateral triangles as much as possible, one thing that immediately came to our mind is the conformal map which transforms between two spaces while preserving angles locally. Thus a good stippling on a uniform area is guaranteed to be mapped to still a good one on a specified non-uniform area.

A simple example of conformal map is a complex holomorphic function

, say

f(z)=z-

exp-

(z-1)

In[155]:=

cmfunc=Compile{{z,_Complex}},Module{w=1.I},w=z-

Exp-

(z-1)

;{Re@w,Im@w},RuntimeOptions"Speed",RuntimeAttributes{Listable},ParallelizationTrue;

which transforms the stippling points refinedPts in the uniform square

[-1,1]×[-1,1]

to a new points distribution transPts:

In[156]:=

transPts=refinedPts.{1,I}//cmfunc;transPts//Graphics[{AbsolutePointSize[2],Point@#}]&

Out[]=

The high quality of refinedPts has been preserved:

In[162]:=

PropertyValue[{DelaunayMesh[transPts],2},MeshCellQuality]//Histogram[#,PlotRange{{0,1},All}]&

Out[]=

It gives this nice non-uniform Voronoi mesh:

In[382]:=

Module[{vm=VoronoiMesh[refinedPts,{{-1,1},{-1,1}}]},Graphics[GraphicsComplex[(Identity@@@MeshPrimitives[vm,0]).{1,I}//cmfunc,vm//MeshCells[#,1]&//Line[Identity@@@#]&]]]

Out[]=

Approach using the weighted Voronoi diagram

Despite the elegance of the conformal mapping, the popular method for stippling non-uniform area comes from a modification of the CVD, which is called the weighted centroidal Voronoi diagram (A. Secord. Weighted Voronoi stippling. In Proceedings of the second international symposium on Non-photorealistic animation and rendering, pages 37–43. ACM Press, 2002.) (A. Secord. Random Marks on Paper, Non-Photorealistic Rendering with Small Primitives, Thesis for the Degree of Master of Science, 2002).

The algorithm is similar to the Lloyd's algorithm, only in step 3, when looking for the centroid of the Voronoi cell, a variable areal density

ρ(P)

is considered, which is proportional to the grayscale at the location

. Thus we shall calculate the centroid according to following formula:

(

)

The integration is quite time-consuming. In his paper and master thesis Secord presented an efficient numerical algorithm, which involves a pre-computation of certain integrations. However, I noticed (without theoretical proof) that the weighted CVD can be sufficiently approximated in a much cheaper way if we accept a compromise not to stick to the exact formula but only to emphasis the core idea of choosing

closer to points with larger weights.

The new idea is simple. For a cell of

vertices

{

,…,

}

, the algorithm acts as follows:

Compute the geometric centroid

Compute the weights of the vertices as

{

,…,

}

Compute normalized weights as

max({

,…,

})

For every vertex

, move it along

with factor of

to new position

′

(So vertex with largest weight does not move, vertex with smallest weight moves most)

Compute the geometric centroid

′

of the new cell defined by

{

′

,…,

′

}

as the final result

Note that the convergence of our simplified algorithm is not obvious, so it might be wise to do an early stop during iteration.

Numerical example

As a demonstration, I’ll use the algorithm to convert the famous photograph of Margaret Heafield Hamilton, who has just been awarded the Presidential Medal of Freedom last month, to stippling drawing.

The photograph used came from Wikipedia:

In[384]:=

img=Import["https://upload.wikimedia.org/wikipedia/commons/2/2e/Margaret_Hamilton.gif"]//ColorConvert[#,"Grayscale"]&//ImageResize[#,1000]&;

With some enhancement (mainly to increase the local contrast), we got the following image, which has a grayscale colorspace with values rescaled to span from 0 to 1.

In[52]:=

imgTest=

data cache

size:

6.02

→

1.06

rate:

0.176

type:

List

;

A high efficient image value retrieving function is defined as following:

In[60]:=

ClearAll[imgVal]SetAttributes[imgVal,HoldFirst]imgVal[img_?ImageQ,pos_,"targetSize"{width_?NumericQ,height_?NumericQ}]:=ImageValue[img,pos,DataRange{{0,width},{0,height}},Resampling"Nearest"]imgVal[img_?ImageQ,pos_]:=imgVal[img,pos,"targetSize"ImageDimensions@img]imgVal[img_?ImageQ,"targetSize"{width_?NumericQ,height_?NumericQ}]:=Function[pos,imgVal[img,pos,"targetSize"{width,height}]]imgVal[img_?ImageQ]:=imgVal[img,"targetSize"ImageDimensions@img]

A dedicated function findCentroid for computing the geometric centroid of any given polygon is defined according to the following formula:

Suppose the polygon is defined by

vertices ordered (counter-)clockwise

{

),…,

)}

, then its centroid

can be determined as

(

)

In[66]:=

Clear[findCentroid]findCentroid=Compile{{pts,_Complex,1}},Block{pairs,dets,area},pairs=Join[Partition[pts,2,1],{pts〚{-1,1}〛}];dets=Re[#〚1〛(Re[#〚2〛]I+Im[#〚2〛])]&/@pairs;area=Total@dets;Ifarea0,

Total@pts

Length@pts

dets.(Total/@pairs)

3area

;

The main body for a single step of CVD relaxing:

In[68]:=

Clear[weightedVoronoiRefineFunc]weightedVoronoiRefineFunc[pts_,range_]:=Module{vm,geomCentroidSet,vtxIdxSet,vtxCoordSet,vtxIdxAsso,densityAsso,polySet,weightSet,polySetNew,ptsNew,vtxIdxAssoRevNew,polyIdxSetNew,degCellIdxSet,centroidShiftSet,vmNew},(*FindingthegeometriccentroidsofeveryVoronoicells:*)vm=VoronoiMesh[ReIm@pts,range];If[Head[vm]===EmptyRegion,Dialog[];Abort[]];geomCentroidSet=PropertyValue[{vm,2},MeshCellCentroid].{1,I};(*ExtractthegeometricinformationoftheVoronoicells:*)vtxIdxSet=MeshCells[vm,0];;,1;polySet=MeshCells[vm,2];;,1;vtxCoordSet=MeshCoordinates[vm];vtxIdxAsso=Thread[vtxIdxSetvtxCoordSet.{1,I}]//Association;(*Extracttheimagevaluesoneveryverticesofeverycells:*)densityAsso=Thread[vtxIdxSetimgVal[imgTest]@vtxCoordSet]//Association;(*computecentroidsofshape-shiftedcellsaccordingtotheCVDalgorithm:*)weightSet=

Max/@#//#-Unitize[#]+1&

&[1-(polySet/.densityAsso)//Chop];polySetNew=weightSet((polySet/.vtxIdxAsso)-geomCentroidSet);centroidShiftSet=findCentroid/@polySetNew;geomCentroidSet+centroidShiftSet

Now an adaptive random initialization can be performed efficiently with the help of imgVal:

In[15]:=

stipplePts=RandomComplex[{0,ImageDimensions[imgTest].{1,I}},

]//Module[{pos=#,val=imgVal[imgTest]@ReIm@#,prob,κ=3,emphasis},prob=RandomReal[1,Length@pos];emphasis=Rescale[Clip[-κ(val-.5)],{-1,1},{-.1,1}];prob-val+emphasis//UnitStep//Pick[pos,#,1]&]&;//AbsoluteTiming//Echo[Quantity[#〚1〛,"Seconds"],"time for sampling: "]&;Echo[stipplePts//Length,"number of points: "];Graphics[{Black,AbsolutePointSize[1],Point@ReIm@stipplePts},PlotRangePaddingNone,ImageSize120]

time for sampling:

0.0484393

number of points: 3834

Out[]=

One step of the CVD relaxing:

In[18]:=

stipplePts=weightedVoronoiRefineFunc[stipplePts,{{1,1},ImageDimensions@imgTest}];//AbsoluteTiming//First//Quantity[#,"Seconds"]&Graphics[{Black,AbsolutePointSize[1],Point@ReIm@stipplePts},PlotRangePaddingNone,ImageSize120]

Out[]=

0.801279

Out[]=

30 more steps of the CVD relaxing:

In[43]:=

Block[{initPts=stipplePts,range={{1,1},ImageDimensions@imgTest},numOfIteration=30},stipplePts=Nest[(stipplePts=weightedVoronoiRefineFunc[#,range])&,initPts,numOfIteration]];//AbsoluteTiming//Echo[Quantity[#〚1〛,"Seconds"],"time consumed: "]&;Graphics[{Black,AbsolutePointSize[1],Point@ReIm@stipplePts},PlotRangePaddingNone,ImageSize120]

time consumed:

15.8399

Out[]=

Further iteration will make no significant difference, but increasing the number of sampling points will do great job:

In[443]:=

Block[{numOfsampling=

,stipplePts,range={{1,1},ImageDimensions@imgTest},numOfIteration=30},(*sampling:*)AbsoluteTiming[stipplePts=RandomComplex[{0,ImageDimensions[imgTest].{1,I}},numOfsampling]//Module[{pos=#,val=imgVal[imgTest]@ReIm@#,prob,κ=3,emphasis},prob=RandomReal[1,Length@pos];emphasis=Rescale[Clip[-κ(val-.5)],{-1,1},{-.1,1}];prob-val+emphasis//UnitStep//Pick[pos,#,1]&]&;]//Echo[Quantity[#〚1〛,"Seconds"],"time for sampling: "]&;Echo[stipplePts//Length,"number of points: "];Echo[numOfIteration,"number of iterations: "];(*iteration:*)AbsoluteTiming[stipplePts=Nest[weightedVoronoiRefineFunc[#,range]&,stipplePts,numOfIteration];]//Echo[Quantity[#〚1〛,"Seconds"],"time consumed for iterations: "]&;Graphics[{Black,AbsolutePointSize[1],Point@ReIm@stipplePts},PlotRangePaddingNone]]

time for sampling:

0.045013

number of points: 37909

number of iterations: 30

time consumed for iterations:

342.568

Out[]=

Now if we using as huge as 377980 points and iterate for 50 times, which took about 6 hours on an ultrabook with an Intel Core i5 CPU, we got the following amazing result:

In[171]:=

stipplePts=

data cache

size:

7.85

→

2.40

rate:

0.306

type:

List

;With[{range={{1,1},ImageDimensions@imgTest},threshold=.1,ptSize=2,size=700,multi=3,finalSize=800},Graphics[{Black,AbsolutePointSize[ptSize],Point@ReIm@#},PlotRangePaddingNone,PlotRangerange,ImageSizeRound[multisize]]&@Pick[stipplePts,UnitStep[imgVal[imgTest]@ReIm@stipplePts-1+threshold],0]//Rasterize[#,ImageSizeRound[multisize]]&//ImageResize[#,finalSize]&]

Out[]=

Inspired by the example under the Properties & Relations section in the documentation of GradientOrientationFilter, a hatching style drawing can be generated by initializing a stroke at each stippling point, with the lengths and orientations controlled by local grayscale and gradient magnitude, respectively:

In[179]:=

Module[{orientation,orientationimg,pos,fraction=.05,basicLength=7,orient,length,strocks},orientation=ImageData[GradientOrientationFilter[imgTest,5]];orientationimg=Image@ArcTan[Sin[orientation],-Cos[orientation]];orientationimg=ColorQuantize[orientationimg,3];pos=RandomSample[stipplePts,Round[fractionLength[stipplePts]]];orient=imgVal[orientationimg]@ReIm@pos;length=basicLength(1-imgVal[imgTest]@ReIm@pos);strocks=lengthIExp[Iorient]//{pos+#,pos-#}&//ReIm;Graphics[{AbsoluteThickness[0],Line@strocks},PlotRangeAll,PlotRangePaddingNone,ImageSize200]]

Out[]=

Sampling more points (by setting a larger fraction) will take longer time but give nicer result:

In[180]:=

Module[{orientation,orientationimg,pos,threshold=.15,fraction=.5,basicLength=5,orient,length,strocks,size=1500,multi=2,finalSize=800},orientation=ImageData[GradientOrientationFilter[imgTest,5]];orientationimg=Image@ArcTan[Sin[orientation],-Cos[orientation]];orientationimg=ColorQuantize[orientationimg,3];pos=RandomSample[stipplePts,Round[fractionLength[stipplePts]]];pos=Pick[pos,UnitStep[imgVal[imgTest]@ReIm@pos-1+threshold],0];orient=imgVal[orientationimg]@ReIm@pos;length=basicLength(1-imgVal[imgTest]@ReIm@pos);strocks=lengthIExp[Iorient]//{pos+#,pos-#}&//ReIm;Graphics[{AbsoluteThickness[0],Line@strocks},PlotRangeAll,PlotRangePaddingNone,ImageSizeRound[multisize]]//Rasterize[#,ImageSizeRound[multisize]]&//ImageResize[#,finalSize]&]

Out[]=

Numerical example 2

Another example can be given from another famous photograph of:

In[105]:=

img=Import["https://upload.wikimedia.org/wikipedia/commons/a/aa/Margaret_Hamilton_in_action.jpg"];imgTest=img//ImageAdjust//HistogramTransform//ImageAdjust[#,{1,-.6,.2}]&//ImageAdjust;imgTest=ImageAdd[imgTest//ColorNegate//ImageMultiply[#,.5]&,ColorToneMapping[img,.5]//ColorNegate//ImageMultiply[#,.3]&,RidgeFilter[img//ColorNegate,1]//ImageAdjust//ImageMultiply[#,.2]&]//ColorNegate//ImageAdjust[#,{0,0,2}]&//ImageAdjust;

With 222591 points taking about 20 iterations, we got the following nice result:

In[191]:=

stipplePts=

data cache

size:

4.63

→

1.37

rate:

0.296

type:

List

;With[{range={{1,1},ImageDimensions@imgTest},threshold=.15,ptSize=3,size=850,multi=3,finalSize=800},Graphics[{Black,AbsolutePointSize[ptSize],Point@ReIm@#},PlotRangePaddingNone,PlotRangerange,ImageSizeRound[multisize]]&@Pick[stipplePts,UnitStep[imgVal[imgTest]@ReIm@stipplePts-1+threshold],0]//Rasterize[#,ImageSizeRound[multisize]]&//ImageResize[#,finalSize]&]

Out[]=

Again we can generate a hatching style drawing from stipplePts:

In[193]:=

Module[{orientation,orientationimg,pos,threshold=.15,fraction=.7,basicLength=3,orient,length,strocks,size=1500,multi=1.5,finalSize=800},orientation=ImageData[GradientOrientationFilter[imgTest,5]];orientationimg=Image@ArcTan[Sin[orientation],-Cos[orientation]];orientationimg=ColorQuantize[orientationimg,3];pos=RandomSample[stipplePts,Round[fractionLength[stipplePts]]];pos=Pick[pos,UnitStep[imgVal[imgTest]@ReIm@pos-1+threshold],0];orient=imgVal[orientationimg]@ReIm@pos;length=basicLength(1-imgVal[imgTest]@ReIm@pos);strocks=lengthIExp[Iorient]//{pos+#,pos-#}&//ReIm;Graphics[{AbsoluteThickness[0],Line@strocks},PlotRangeAll,PlotRangePaddingNone,ImageSizeRound[multisize]]//Rasterize[#,ImageSizeRound[multisize]]&//ImageResize[#,finalSize]&]

Out[]=

Cite this as: Silvia Hao, "Stippling portrait of Margaret Heafield Hamilton" from the Notebook Archive (2016), https://notebookarchive.org/2019-02-2rwx0u4

​ A Wolfram Notebook on Stippling Drawing

Introduction

The essential properties of a good stippling

Get started -- stippling of a uniform area

Advanced -- stippling of a non-uniform area

Approach using the conformal mapping

Approach using the weighted Voronoi diagram

Numerical example

Numerical example 2

A Wolfram Notebook on Stippling Drawing