qwalala_some.nb
Author
Maria Mannone
Title
qwalala_some.nb
Description
Supplemental notebook to "A musical reading of a contemporary installation and back: mathematical investigations of patterns in Qwalala"
Category
Academic Articles & Supplements
Keywords
glass, pattern, gestures, contour, music theory, compositions
URL
http://www.notebookarchive.org/2021-02-bzzq67w/
DOI
https://notebookarchive.org/2021-02-bzzq67w
Date Added
2021-02-26
Date Last Modified
2021-02-26
File Size
15.3 megabytes
Supplements
Rights
Redistribution rights reserved

Mathematica code for “A musical reading of a contemporary installation and back: mathematical investigations of patterns in Qwalala” and “Venice: Qwalala and other contemporary glassworks in light of categories”
Mathematica code for “A musical reading of a contemporary installation and back: mathematical investigations of patterns in Qwalala” and “Venice: Qwalala and other contemporary glassworks in light of categories”
M. Mannone
ECLT, Ca’ Foscari University of Venice, Italy
Department of Mathematics and Computer Sciences, University of Palermo, Italy
Abstract of the 1st paper
ECLT, Ca’ Foscari University of Venice, Italy
Department of Mathematics and Computer Sciences, University of Palermo, Italy
Abstract of the 1st paper
Mathematical music theory helps us investigate musical compositions in mathematical terms. Some hints can be extended towards the visual arts. Mathematical approaches can also help formalize a “translation” from the visual domain to the auditory one and vice versa. Thus, a visual artwork can be mathematically investigated, then translated into music. The final, refined musical rendition can be compared to the initial visual idea. Can an artistic idea be preserved through these changes of media? Can a non-trivial pattern be envisaged in an artwork, and then still be identified after the change of medium? Here, we consider a contemporary installation and an ensemble musical piece derived from it. We first mathematically investigate the installation, finding its patterns and structure, and then we compare them with structure and patterns of the musical composition. In particular, we apply two concepts of mathematical music theory, the Quantum GestART and the gestural similarity conjecture, to the analysis of Qwalala, realized for the Venice Biennale by Pae White, comparing it to its musical rendition in the homonymous piece for harp and ensemble composed by Federico Favali. Some sketches of generalizations follow, with the “Souvenir Theorem” and the “Art Conjecture.”
Description.
The building glass blocks of installation “Qwalala” are modeled through de Jong attractor’s visualizations, with a suitable choice of parameters and colors, embedded within transparent parallelepipeds.
There is a related topic on Wolfram Demonstration: https://demonstrations.wolfram.com/PeterDeJongAttractors/
The code presented in this notebook is a variation from the code written by user Gleno and published here: https://mathematica.stackexchange.com/questions/50839/smooth-peter-de-jong-attractor
Details of two bricks. Pictures by M. Mannone.
Description.
The building glass blocks of installation “Qwalala” are modeled through de Jong attractor’s visualizations, with a suitable choice of parameters and colors, embedded within transparent parallelepipeds.
There is a related topic on Wolfram Demonstration: https://demonstrations.wolfram.com/PeterDeJongAttractors/
The code presented in this notebook is a variation from the code written by user Gleno and published here: https://mathematica.stackexchange.com/questions/50839/smooth-peter-de-jong-attractor
Details of two bricks. Pictures by M. Mannone.



(*originalfunction"func"writtenbyuserGlenoandpublishedhere:https://mathematica.stackexchange.com/questions/50839/smooth-peter-de-jong-attractor*)
func=Compile[{{dim,_Integer},{params,_Real,1},{iters,_Integer}},Module[{matrix,d1,d2,a,b,c,d,x,y,iter,xp,xn,yp,yn,max},matrix=Table[0.0,{dimdim}];{a,b,c,d,x,y,iter}=params~Join~{0,0,1};{d1,d2}={1+0.5(dim-1),0.25(dim-1)};While[++iter<iters,xn=Sin[ay]-Cos[bx];y=Sin[cx]-Cos[dy];x=xn;xp=Floor[d1+d2x];yp=Floor[d1-d2y];++matrix[[ypdim+xp]];];max=Max@matrix;Partition[(Sqrt[#]/max&)/@matrix,dim]],CompilationTarget"C",RuntimeOptions"Speed"];
(*Redblock*)
dejong2[dim_,params_,iters_]:=Module[{matrix},matrix=func[dim,params,iters];Colorize[ArrayPlot[matrix,ImageSizedim,FrameFalse],ColorFunctionColorData["CherryTones"]]];dejong2[1024,{10.5,−2,0.7,−1},20000000]

RedPattern=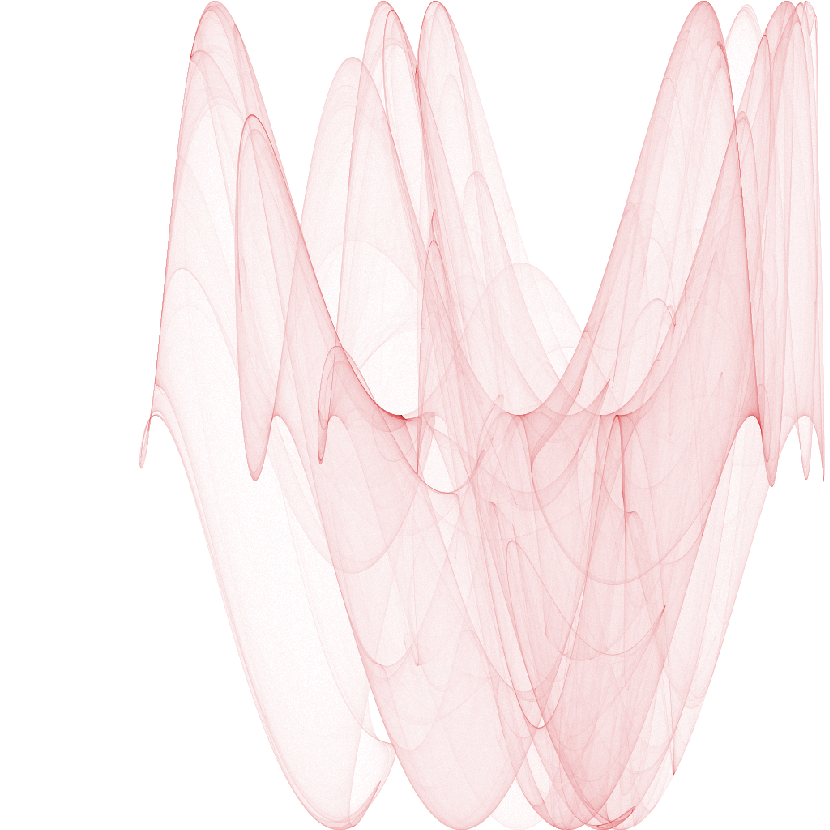

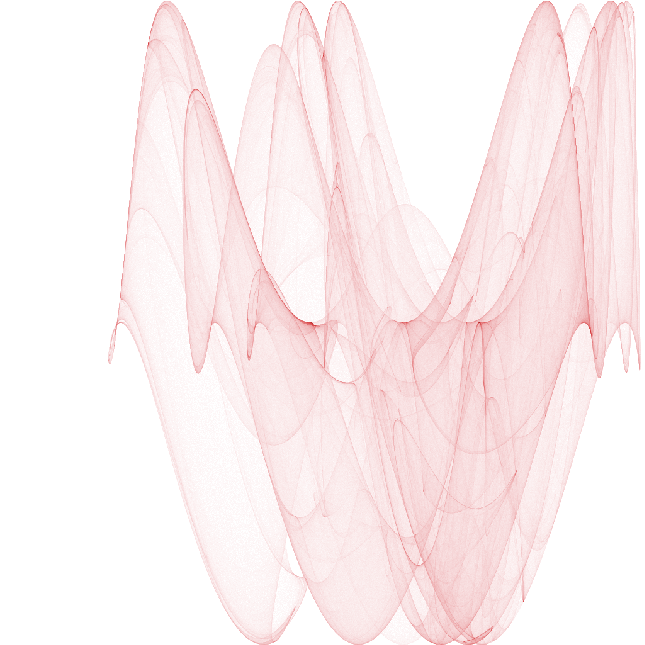
RedPatternBetter=RemoveBackground[RedPattern,{"Background",{"Uniform",0.08}}]
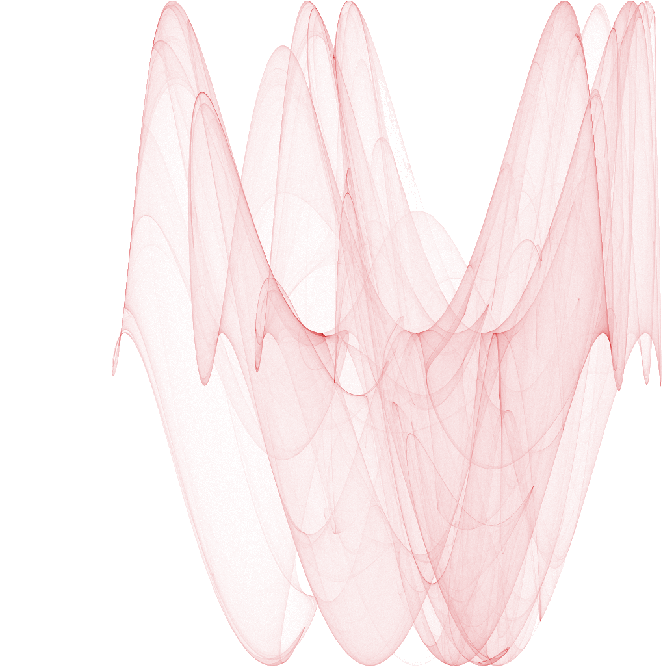
Graphics3D[{EdgeForm[White],FaceForm[Red],Opacity[.05],Cuboid[{-1,1,-1},{0.001,0.001,0.025}]},BoxedFalse]
Graphics3D[{EdgeForm[White],FaceForm[Red],Opacity[.05],Cuboid[{-1,1,-1},{0.001,0.001,0.025}],Inset[RedPatternBetter,{-0.5,.5,-0.5},Automatic,240,{{-2,0},{0,1}}]},BoxedFalse]
(*Blueblock*)
Graphics3D[{EdgeForm[LightBlue],FaceForm[LightBlue],Opacity[.05],Cuboid[{-1,1,-1},{0.001,0.001,0.025}]},BoxedFalse]
dejong2[dim_,params_,iters_]:=Module[{matrix},matrix=func[dim,params,iters];Colorize[ArrayPlot[matrix,ImageSizedim,FrameFalse],ColorFunctionColorData["DeepSeaColors"]]];dejong2[1024,{10.5,−2,0.7,−1},20000000]

BluePattern=


BluePatternBetter=RemoveBackground[BluePattern,{"Background",{"Uniform",0.08}}]

Graphics3D[{EdgeForm[LightBlue],FaceForm[Blue],Opacity[0.09],Cuboid[{-1,1,-1},{0.001,0.001,0.025}],Inset[BluePatternBetter,{-0.5,.5,-0.5},Automatic,240,{{-2,0},{0,1}}]},BoxedFalse]
Cite this as: Maria Mannone, "qwalala_some.nb" from the Notebook Archive (2021), https://notebookarchive.org/2021-02-bzzq67w
Download
