EVS-SR-notebook.nb
Author
Prashant Singh, Arnab Pal
Title
EVS-SR-notebook.nb
Description
Supplemental notebook to "Extremal statistics for stochastic resetting systems"
Category
Academic Articles & Supplements
Keywords
non-equilibrium system, extreme value statistics, evs, stochastic resetting systems, Markov
URL
http://www.notebookarchive.org/2021-04-dtvedbl/
DOI
https://notebookarchive.org/2021-04-dtvedbl
Date Added
2021-04-30
Date Last Modified
2021-04-30
File Size
0.55 megabytes
Supplements
Rights
Redistribution rights reserved

Supplemental notebook
Supplemental notebook
Prashant Singh
International Centre for Theoretical Sciences, TIFR, Bengaluru 560089, India
Arnab Pal
School of Chemistry, The Center for Physics and Chemistry of Living Systems, Tel Aviv University, Tel Aviv 6997801, Israel
Abstract: In this notebook, we provide some of the detailed derivations for the numerical calculations used in our submitted preprint: arXiv:2102.07111 “Extremal statistics for stochastic resetting systems”.
Dated: April 28, 2021
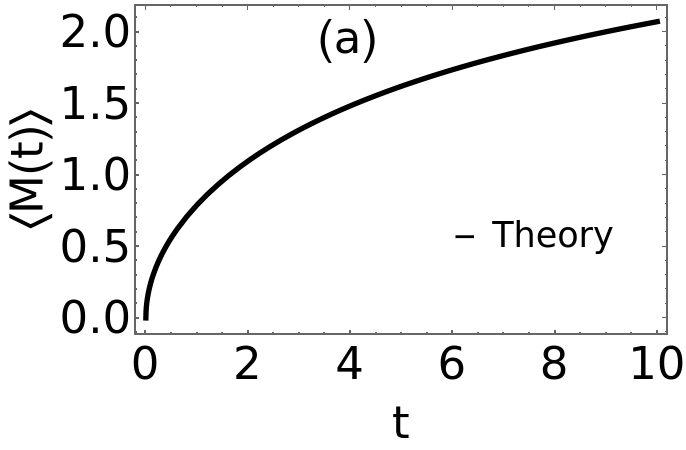
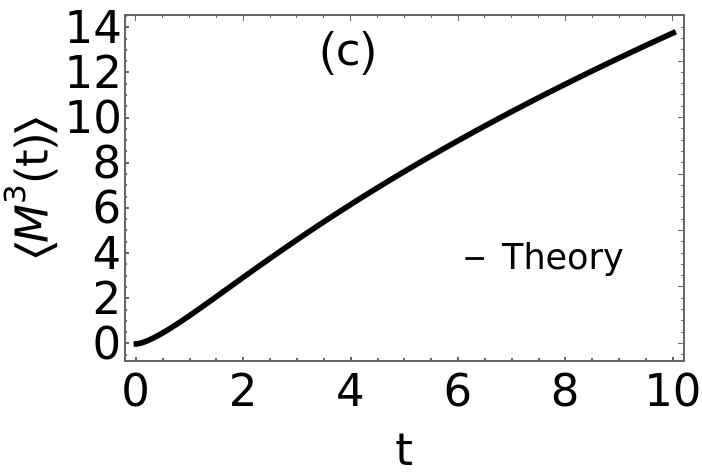
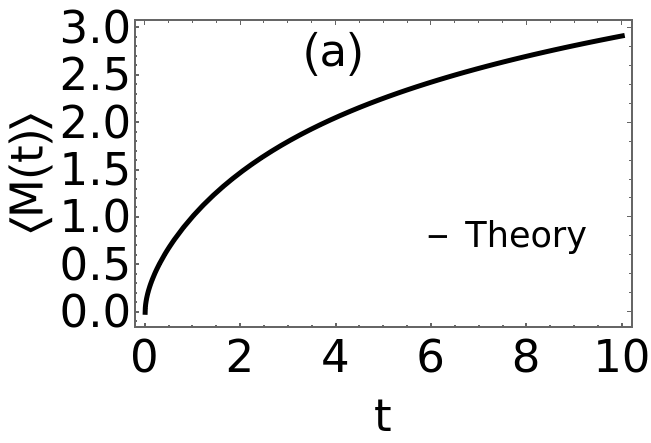
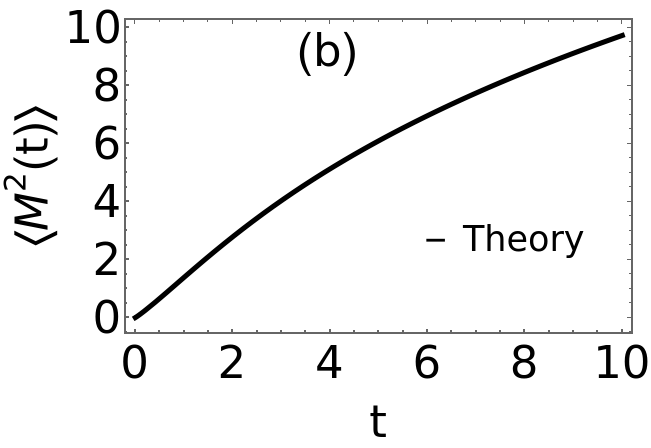
(1)MomentsofMfordiffusion;H[z_,n_]:=n!SumHypergeometric1F1Regularized-1+,k+,-z,{k,1,102}momBM[n_,r_,t_]:=H[rt,n]t0=5;r0=1;B1=Plot[{momBM[1,r0,t]},{t,0,10},PlotStyle{Thickness[0.01],Black},FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"t","〈M(t)〉"},LabelStyleDirective[Black,45],PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.75,.3}],Epilog{Text[Style["(a)",Black,45],Scaled[{.4,.9}]],Text[Style["",Black,45],Scaled[{.5,.3}]]}]B2=Plot[{momBM[2,r0,t]},{t,0,10},PlotStyle{Thickness[0.01],Black},FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"t","〈(t)〉"},LabelStyleDirective[Black,45],PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.75,.3}],Epilog{Text[Style["(b)",Black,45],Scaled[{.4,.9}]],Text[Style["",Black,45],Scaled[{.5,.3}]]}]B3=Plot[{momBM[3,r0,t]},{t,0,10},PlotStyle{Thickness[0.01],Black},FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"t","〈(t)〉"},LabelStyleDirective[Black,45],PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.75,.3}],Epilog{Text[Style["(c)",Black,45],Scaled[{.4,.9}]],Text[Style["",Black,45],Scaled[{.5,.3}]]}]
-n
2
(-1)
k+-1
n
2
(-z)
n
k
n
2
n
2
1
n
2r
2
M
3
M

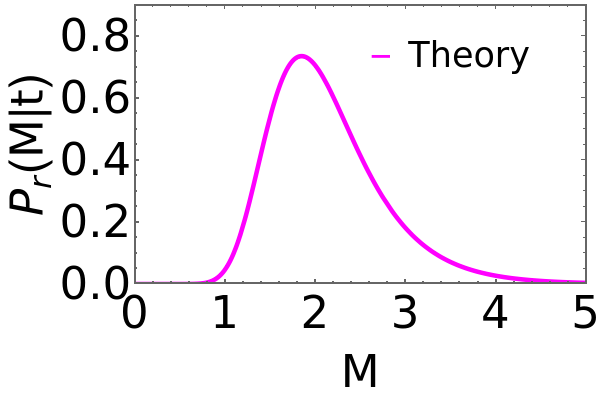
(2)DistributionofMfordiffusion;PmaxBM[r_,t_,M_]:=tExp[-(M|t)"},LabelStyleDirective[Black,45],PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.7,.82}]]
2
3
2
r
2r
M]Exp[-rtExp[-2r
M]]t0=20;r0=2;A1=Plot[PmaxBM[r0,t0,M],{M,0,t0},PlotRange{{0,5},{0,0.9}},PlotStyle{Thickness[0.01],Magenta},FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"M","P
r
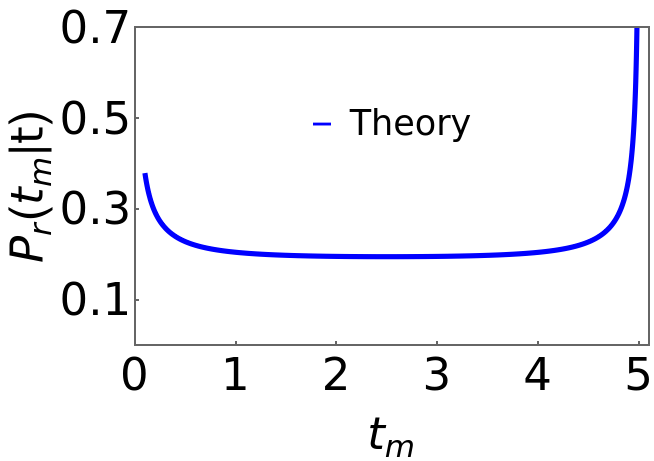
(3)Distributionoftmfordiffusion;r0=1;t0=5;ZZ[tm_]:=r0Exp[-r0t0]NIntegratewExp[r0t0w]Erf[-1+HypergeometricPFQ{1,1},,2,r0(t0-tm)+HypergeometricPFQ{1,1},,2,r0tm+C2=Plot[ptmBM[tm],{tm,0.1,t0},PlotRange{{0,t0+0.1},{0,0.7}},PlotStyle{Thickness[0.01],Blue},FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"","(|t)"},LabelStyleDirective[Black,45],PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.5,.7}],FrameTicks{{{0.1,0.3,0.5,0.7},None},{{0,1,2,3,4,5},None}}]
r0tmw
]Erfr0w(t0-tm)
,{w,0,1}ptmBM[tm_]:=ZZ[tm]+Exp[-r0t0]
π
tm(t0-tm)
1
2
1
2
Log[r0t0]
2r0
2
t0
t
m
P
r
t
m
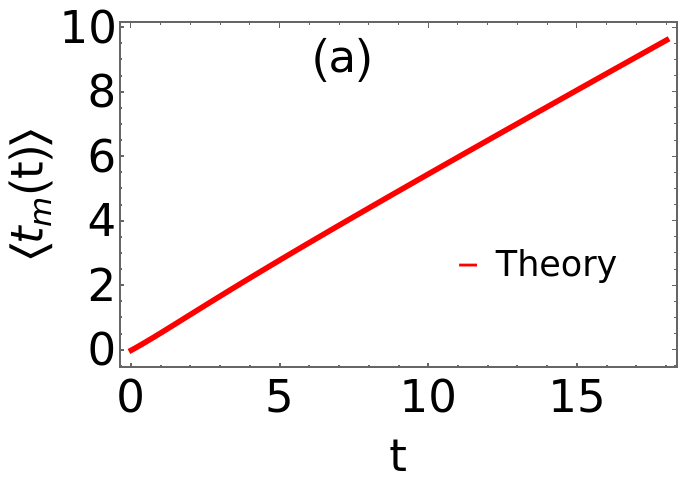
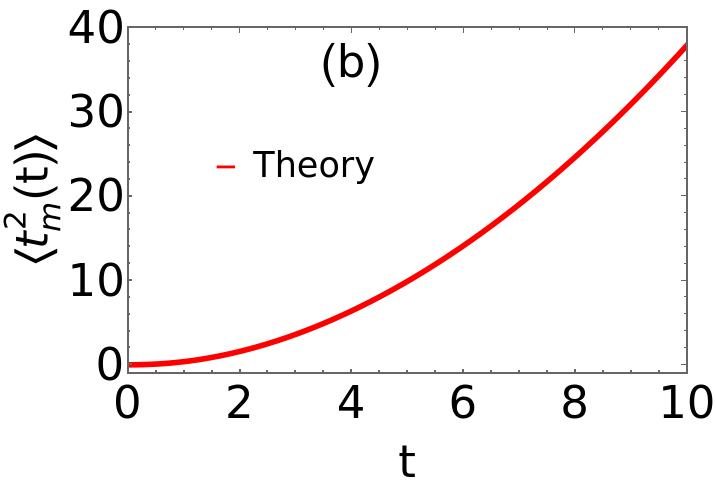
(4)Firsttwomomentsoftmfordiffusion;r0=1;momtm1[r_,t_]:=(2rt+Exp[-rt]-1+EulerGamma+Gamma[0,rt]+Log[rt])momtm2[r_,t_]:=((9+5rt)Exp[-rt]-9+4rt(1+2rt)+4-3EulerGamma-3Gamma[0,rt]-3Log[rt]+4rt(-1+EulerGamma+Gamma[0,rt]+Log[rt])+Exp[-rt](-4-3EulerGamma+3CosIntegral[rt]+3SinhIntegral[rt]-3Log[rt]))+NIntegrate[yExp[y]HypergeometricPFQ[{1,1,1},{2,2,2},-y],{y,0,rt}]Q1=Plot[{momtm1[r0,t]},{t,0,18},PlotStyle{Thickness[0.01],Red},PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.75,.3}],FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"t","〈(t)〉"},LabelStyleDirective[Black,45],Epilog{Text[Style["(a)",Black,45],Scaled[{.4,.9}]],Text[Style["",Black,45],Scaled[{.5,.3}]]}]Q2=Plot[momtm2[r0,t],{t,0,10},PlotStyle{Thickness[0.01],Red},PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.3,.6}],FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"t","〈(t)〉"},LabelStyleDirective[Black,45],PlotRange{{0,10},{-1,40}},Epilog{Text[Style["(b)",Black,45],Scaled[{.4,.9}]],Text[Style["",Black,45],Scaled[{.5,.3}]]}]
1
4r
1
24
2
r
Exp[-rt]
12
2
r
t
m
2
t
m
(5)MomentsofMfordrifteddiffusion;Term[y_,w_,n_]:=D[xExp[w]Erfc[x)w]+z-Term[y,w,n],{w,0,1}ScaHH[z_,y_,n_]:=nSumSSu[k,n,z,y],{k,1,30}momnMdBM[n_,r_,t_,v_]:=ScaHHrt,-v,nv0=0.5;r0=1.0;BB1=Plot[momnMdBM[1,r0,t,v0],{t,0,10},PlotStyle{Thickness[0.01],Black},FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"t","〈M(t)〉"},LabelStyleDirective[Black,45],PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.75,.3}],Epilog{Text[Style["(a)",Black,45],Scaled[{.4,.9}]],Text[Style["",Black,45],Scaled[{.5,.3}]]}]BB2=Plot[momnMdBM[2,r0,t,v0],{t,0,10},PlotStyle{Thickness[0.01],Black},FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"t","〈(t)〉"},LabelStyleDirective[Black,45],PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.75,.3}],Epilog{Text[Style["(b)",Black,45],Scaled[{.4,.9}]],Text[Style["",Black,45],Scaled[{.5,.3}]]}]BB3=Plot[momnMdBM[3,r0,t,v0],{t,0,10},PlotStyle{Thickness[0.01],Black},FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"t","〈(t)〉"},LabelStyleDirective[Black,45],PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.75,.3}],Epilog{Text[Style["(c)",Black,45],Scaled[{.4,.9}]],Text[Style["",Black,45],Scaled[{.5,.3}]]}]
2
x
w
],{x,n-1}]/.xySSu[k_,n_,z_,y_]:=NIntegrateExp[-(z+2
y
k-1
(1-w)
Gamma[k]
k
(1-w)
Gamma[k+1]
HeavisideTheta[1.5-n]
πw
n
(-1)
z
k
(-z)
n
k
n
2
t
2
t
2
2
M
3
M

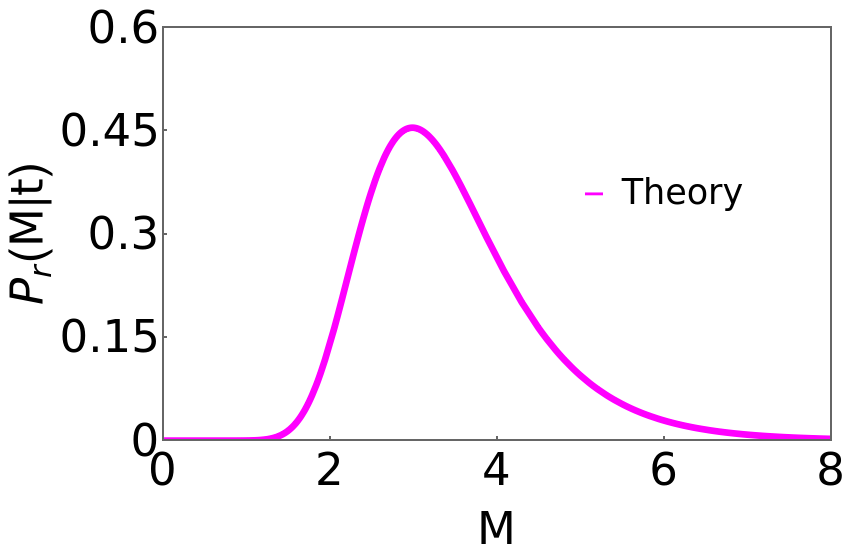
(6)DistributionofMfordrifteddiffusion;PMdBM[v_,r_,t_,α_,M_]:=rαtExp[-Mα]Exp[-rtExp[-Mα]]v0=1;r0=2;t0=20;α0=+2r0-v0;E1=Plot[PMdBM[v0,r0,t0,α0,M],{M,0,10},PlotRange{{0,8},{0,0.6}},PlotStyle{Thickness[0.01],Magenta},FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"M","(M|t)"},LabelStyleDirective[Black,45],PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.75,.6}],Epilog{Text[Style["",Black,45],Scaled[{.4,.9}]],Text[Style["",Black,45],Scaled[{.5,.3}]]},FrameTicks{{{0,0.15,0.3,0.45,0.6},None},{{0,2,4,6,8},None}}]
2
v0
P
r
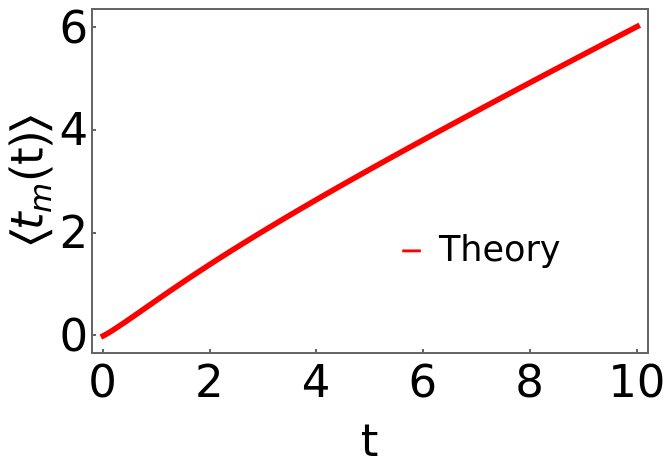
(7)Meantmfordriftdiffusionprocess;r0=1;v0=1;D0=0.5;II1[t_]:=2r0t+Exp[-r0t]Erfcv0++4D0r0Erf+4D0r0t-1J1[t_]:=(EulerGamma+Gamma[0,r0t]+Log[r0t])II2[t_]:=J1[t]+NIntegrateJ1[τ]v0,{τ,0,t}meantm[t_]:=II1[t]+II2[t]X1=Plot[{meantm[t]},{t,0,10},PlotStyle{Thickness[0.01],Red},FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"t","〈(t)〉"},LabelStyleDirective[Black,45],PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.7,.3}],Epilog{Text[Style["",Black,45],Scaled[{.4,.9}]],Text[Style["",Black,45],Scaled[{.5,.3}]]},FrameTicks{{{0,2,4,6},None},{{0,2,4,6,8,10},None}}]
1
4r0
t
4D0
v0
2
v0
2
v0
4D0
1
4r0
Exp-+4D0r0(t-τ)
2
v0
4D0
4πD0(t-τ)
t
m
(8)Distributionoftmfordriftdiffusionprocess;r0=1.5;t0=5;v0=1;D0=0.5;I1[tm_]:=+1HypergeometricPFQ{1,1},,2,+r0(t0-tm)-HypergeometricPFQ{1,1},,2,(t0-tm)-I2[tm_]:=-+NIntegrateExp[r0t0w],+1I3[tm_]:=+1HypergeometricPFQ{1,1},,2,+r0tm-HypergeometricPFQ{1,1},,2,tm-1+Exp-+r0t0NIntegrateExp[r0t0w]Erf[,w,,+1JJ[tm_,w_]:=-v0Exp[-r0w(t0-tm)]++Exp[-r0w(t0-tm)]+r0(1-w)Erf+Exp[-r0wtm]++r0(1-w)Erf+r0(1-w)tmExp[-r0tmw]JJ[tm,w],{w,0,1}+L1=Plot[{ProbtmdBM[tm]},{tm,0.1,t0},PlotRange{{0,t0+0.1},{0,0.7}},PlotStyle{Thickness[0.01],Blue},FrameStyleThick,FrameTrue,FrameStyleThick,FrameLabel{"","(|t)"},LabelStyleDirective[Black,45],PlotLegendsPlaced[LineLegend[{"Theory"},LabelStyle{FontSize35}],{.6,.5}],Epilog{Text[Style["",Black,45],Scaled[{.4,.9}]],Text[Style["",Black,45],Scaled[{.5,.3}]]},FrameTicks{{{0,0.2,0.4,0.6},None},{{0,1,2,3,4,5},None}}]
Exp-+r0t0
2
v0
2
π
tm(t0-tm)
2
v0
2r0
1
2
2
v0
2
2
v0
2r0
1
2
2
v0
2
v0Exp-+r0tm
2
v0
2
2πtm
1-Exp[-r0(t0-tm)]
r0(t0-tm)
v0Exp-+r0(t0-tm)
2
v0
2
2π(t0-tm)
1-Exp[-r0tm]
r0tm
2
v0
2
1-Exp[-r0t0]
r0t0
v0Exp-+r0t0
2
v0
2
2
r0w
Erfr0w(t0-tm)
,w,2
v0
2r0
2
v0
2r0
Exp-+r0t0
2
v0
2
π
tm(t0-tm)
2
v0
2r0
1
2
2
v0
2
2
v0
2r0
1
2
2
v0
2
2
v0
2
r0tmw
]r0wErfr0w(t0-tm)
-v0
2
2
v0
2r0
2
v0
2r0
4D0
Exp-+r0(t0-tm)
2
v0
4D0
π(t0-tm)
2
v0
4D0
(t0-tm)+r0-r0w
ProbtmdBM[tm_]:=NIntegrate2
v0
4D0
Exp-+r0tm
2
v0
4D0
4πD0tm
v0
4D0
2
v0
4D0
4D0
2
v0
4D0
1
(+2r0)
2
v0
(+2r0)
-v02
v0
Log[r0t0]
2
t0
t
m
P
r
t
m

Cite this as: Prashant Singh, Arnab Pal, "EVS-SR-notebook.nb" from the Notebook Archive (2021), https://notebookarchive.org/2021-04-dtvedbl
Download
