Fundamentals of thin lenses
Author
Julian Laverde
Title
Fundamentals of thin lenses
Description
Mathematical fundamentals of thin lenses using LensManipulate
Category
Essays, Posts & Presentations
Keywords
Optics, Physics, Lens
URL
http://www.notebookarchive.org/2021-05-blad4yn/
DOI
https://notebookarchive.org/2021-05-blad4yn
Date Added
2021-05-25
Date Last Modified
2021-05-25
File Size
1.53 megabytes
Supplements
Rights
Redistribution rights reserved

Fundamentals of thin lenses
Fundamentals of thin lenses
Julián Laverde
Special Projects, Wolfram Research
What are Thin Lens?
What are Thin Lens?
A thin lens is a lens that its thickness along the optical axis (the line along all surfaces are rotational symmetric) is negligible compared to the radii of curvature of the lens surfaces thus ignoring the refractive effects due to the propagation of light inside the lens. Most often lenses have two or more refractive surfaces and generally, the nonplanar surfaces are spherical segments.
To study the effects of thin lenses, let me consider simple lenses (lenses that have only two refractive surfaces) and begin by discussing the refraction at a single spherical interface by means of the Fermat’s principle.
Fermat’s principle and refraction at spherical interfaces
Fermat’s principle and refraction at spherical interfaces
In 1657 Pierre de Fermat established a principle for the propagation of light rays: The principle of least time. From this principle, both the law of reflection and the law of refraction can be deduced using only algebraic arguments. To state this principle, Fermat introduced the notion of optical path length (OPL), which involves the refractive index of the medium in determining the length of the light ray. Thus, the principle of minimum time establishes that, to propagate between two points in space, including reflections or refractions at an interface, light travels the path that takes the minimum time (at present it is known that this principle is very restrictive, that is, it does not include all the observed cases; its greater generality is reached by modifying the minimum time condition for that of stationary time).
Fermat’s principle:
δ(OPL)=δn(s)s=0
b
∫
a
The identification of the path followed by the light is carried out by applying a standard algebraic process of optimization of a function by means of derivatives. If it is applied to the case of refraction on a spherical interface, that is to the propagation of an arbitrary ray coming from a source at the fixed point S and refracted towards the fixed point P passing through an arbitrary point A on a spherical surface of radius R centered in C and vertex V, the path of minimum time is the one formed by the incident and refracted rays that satisfy the law Snellius refraction Sin[]Sin[].
n
1
ϕ
i
n
2
ϕ
t
In[]:=

By using the law of cosines, the OPL can be rewritten in such way that via the Fermat’s principle we can have
Apply the Fermat’s principle:
In[]:=
fermatPrincSol=SolveR(+R)Sin[θ]-R(-R)Sin[θ]0,
n
1
s
o
2
l
o
n
2
s
i
2
l
i
s
o
Out[]=
s
o
-R-R+
l
i
n
1
l
o
n
2
l
o
n
2
s
i
l
i
n
1
Assuming that A is close to V the expression for and yield ≈ and ≈ so
l
o
l
i
l
o
s
o
l
i
s
i
Introduce the paraxial approximation:
In[]:=
fermatPrincSol/.{,}//FullSimplify
l
o
s
o
l
i
s
i
Out[]=
-R+(-R+)
s
o
n
2
s
i
s
o
n
1
s
i
Usually written as
n
1
s
o
n
2
s
i
n
2
n
1
R
This is known as the paraxial approximation and delineates the domain of the called first-order theory. Rays that approach the surface at shallow angles (that is ) are known as paraxial rays. It was the mathematician and physicist Carl Gauss in 1841 the first to use this approximation to use this approximation in the technique later known as Gaussian optics or Paraxial optics in which only paraxial rays are considered and optical surfaces are exclusively either flat or portions of a sphere.
Sin[θ]≈θ
The thin lens approximation
The thin lens approximation
Now, for a lens consisting of two refractive surfaces and a paraxial ray, the previous equation describes the imaging formation from the first surface that light encounters of radius . Assuming that lens of refractive index is surrounded by a medium of refractive index , then
R
1
n
l
n
m
n
m
s
o1
n
l
s
i1
n
l
n
m
R
1
After refracting on the first surface, the ray then encounters the second surface and refracts so that ≡- where the negative sign arouses from the sign convention. Thus, the same equation applied to the refraction on the second surface of radius is
s
o2
s
i1
R
2
n
l
-
s
i1
n
m
s
i2
n
m
n
l
R
2
Adding these two equations,
n
m
s
o1
n
m
s
i2
n
l
n
m
R
1
n
m
n
l
R
2
and if the medium surrounding the lens is air ≈1 and omitting the unnecessary subscripts, then we get
n
m
Define the Lens-maker Formula:
In[]:=
lensMakerFormula=+(-1)-
1
s
o
1
s
i
n
l
1
R
1
1
R
2
Out[]=
1
s
i
1
s
o
n
l
1
R
1
1
R
2
known as the Thin-lens Equation or Lens-maker’s Formula.
Gaussian Lens Formula
Gaussian Lens Formula
For a thin lens we can define the inverse focal length as
1/f
Define the inverse focal length:
In[]:=
inverseFocalLength=(-1)-;
n
l
1
R
1
1
R
2
Therefore,
Get the thin lens formula by replacing the definition of the focal length:
In[]:=
lensFormula=lensMakerFormula/.focalLength1/f
Out[]=
1
s
i
1
s
o
n
l
1
R
1
1
R
2
This equations is known as the Gaussian Lens Formula.
The quantities mentioned follow a sign convention for spherical refracting surfaces and thin lenses when light is coming from the left (Table 5.1 from [3]):

Ray diagrams and image formation
Ray diagrams and image formation
The Gaussian Lens Formula dictates the behavior of paraxial rays refracted by a thin lens. Certain rays follow simple rules thus are useful to draw a representation of the path that light rays take to get from an object to its image formed by the lens (where the rays coming from the object converge). This representation is known as ray diagram and is used to explain and predict the location, size, orientation, and type of image formed by a lens depending on the same properties of the object.
In the Wolfram Function Repository there is a resource function named LensManipulate, useful to create a dynamic ray diagram of thin a lens. Let me briefly examine this function.
In the Wolfram Function Repository there is a resource function named LensManipulate, useful to create a dynamic ray diagram of thin a lens. Let me briefly examine this function.
LensManipulate resource function
LensManipulate resource function
LensManipulate generates a graphics object of the ray diagram of a thin lens in which the thin lens parameters can be manipulated dynamically. The function takes as inputs properties of the object like its position and size (relative to the lens size) and the focal length of the lens, and uses the Gaussian Lens Formula to calculate the position of the image and the magnification defined as which indicates the size and orientation of the image. This function uses the same sign convention showed previously.
-
s
i
s
o
To use this function run ResourceFunction[“LensManipulate”] without arguments to use the default values:
Get a manipulable ray diagram of a this lens using the LensManipualte resource function:
In[]:=
ResourceFunction["LensManipulate"][]
Out[]=
The function can also take an Association with the initial values as input, as well as the options of Graphics and others graphical options for instance, to specify the color of the rays or to hide the equations in the ray diagram.
Get a manipulable ray diagram using initial values and some of the options of LensManipulate:
In[]:=
|
Out[]=

Currently, the type of thin lenses available for LensManipulate are the Biconvex and the Biconcave lenses. So, let’s use this function to examine the behaviour of the three principal rays that follow simple rules from the Gaussian Lens Formula, starting with the biconvex lens, a converging (or positive) type of lens that comprises two convex spherical surfaces.
Biconvex thin lens
Biconvex thin lens
One of the principals rays is the parallel ray which is parallel to the optical axis ). Let’s visualize the behaviour of this ray:
(=∞
s
o
Visualize the refraction of a parallel ray due to a biconvex lens
In[]:=
|
Out[]=

Notice that after passing through then lens, the parallel ray is refracted towards the focal point on the other side. Now, let’s consider a ray that passes through the focal point and then reaches the lens:
Visualize the refraction of a focal ray due to a biconvex lens
In[]:=
|
Out[]=

As expected, after being refracted by the lens, the ray emerges parallel to the optical axis . This is an indication of the Principle of Reversibility which presumes that if a ray of light is reversed, it will retrace its path, e.g a parallel ray coming from the image would be refracted towards the focal point in the object space by the lens.
(=∞)
s
i
Finally, let's consider a ray passing through the center of the lens:
Visualize the refraction of a ray passing through the center of a biconvex lens
In[]:=
|
Out[]=

As we can see, this ray does not change its direction after passing through the lens.
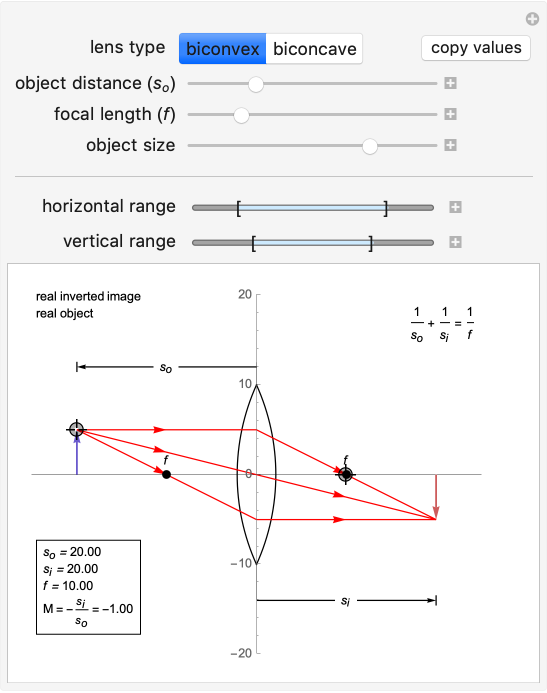
After considering the path followed by these principal rays, we can find the position, size, type and orientation of the image where all rays converge. For a biconvex lens, if the object distance is greater than the focal length, an inverted image is formed in the image space, thus called a real image.
Visualize the formation of a real image formed by a biconvex lens:
In[]:=
|
Out[]=

But in case the object distance is lesser than the focal length, the rays will diverge from an upright virtual image formed in the object space where the rays diverge from:
Visualize the formation of a virtual image formed by a biconvex lens:
In[]:=
|
Out[]=

Biconcave thin lens
Biconcave thin lens
Let’s now consider the case of a biconcave thin lens, a diverging (or negative) type of lens that comprises two concave spherical surfaces. The principal rays follow the same rules considering that this type of lens is diverging. For instance, let’s visualize the behaviour of the parallel ray passing through a biconcave thin lens:
Visualize the refraction of a parallel ray due to a biconcave lens
In[]:=
|
Out[]=

We can see that the parallel ray is refracted so it diverges from the focal point. In other words, the projection of the ray passes through the object focal point. Now, a focal ray converging towards the image focal point, is refracted so it emerges parallel to the optical axis as well as its projection.
(=∞)
s
i
Visualize the refraction of a focal ray due to a biconcave lens
In[]:=
|
Out[]=

Finally, a ray passing through the center of the lens, behaves the same as for the biconvex lens so it does not change its direction:
Visualize the refraction of a ray passing through the center of a biconcave lens
In[]:=
|
Out[]=

After examining the three principal rays, we can deduce that their diverging behaviour of the biconcave lens will always form a virtual image regarding of the position of the object with respect to the focal point:
Visualize the formation of a virtual image formed by a biconcave lens:
In[]:=
|
Out[]=

References
References
1
. Verma, RL (1969), “Al-Hazen: father of modern optics”, Al-‘Arabi, 8: 12–3, PMID 11634474
2
. George Sarton, Introduction to the History of Science, Vol. 1, p. 710.
3
.Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. § 5.2.3. ISBN 0-201-11609-X.
4
.Saleh, B.E.A. (2007). Fundamentals of Photonics (2nd ed.). Wiley.
Cite this as: Julian Laverde, "Fundamentals of thin lenses" from the Notebook Archive (2021), https://notebookarchive.org/2021-05-blad4yn
Download
