Two periodically driven interacting qubits
Author
Michele Delvecchio
Title
Two periodically driven interacting qubits
Description
Mathematica notebook for computing the fidelity, after one period, of two periodically driven interacting qubits
Category
Academic Articles & Supplements
Keywords
Quantum Mechanics, quantum control, quantum computing
URL
http://www.notebookarchive.org/2021-06-bjbq4hz/
DOI
https://notebookarchive.org/2021-06-bjbq4hz
Date Added
2021-06-25
Date Last Modified
2021-06-25
File Size
0.65 megabytes
Supplements
Rights
CC BY 4.0

Two periodically driven interacting qubits
Two periodically driven interacting qubits
In this notebook we simulate a quantum system composed of two qubits, simultaneously driven by an external periodic field Ω affected by imperfection ϵ. The system is described by the Hamiltonian in the time interval , during which the two qubits are cyclically excited, and by that, during the time , describe a long-range dipole interaction between the excited states of the qubits. Such an interaction will correct the errors introduced by the driving field Ω, which is the main result of our work. The analysis is performed by computing the state of the system after one period and deriving the analytical expression of the fidelity , namely the population of the ground state of only one qubit, as a function of the interaction and the error . For a better precision, we finally plot the infidelity in a logarithmic scale.
Η
1
T
1
H
2
T
2
V
T=2+2
T
1
T
2
F
V
ϵ
I=1-F
The result has been used in the paper “Atomic interactions for qubit-error compensations” available in the arXiv:
The result has been used in the paper “Atomic interactions for qubit-error compensations” available in the arXiv:
Definitions of all the variables and parameters
Definitions of all the variables and parameters
Initial state of the system and some shortcuts for the Pauli matrices
In[]:=
psi0=KroneckerProduct[{{0},{1}},{{0},{1}}];id=IdentityMatrix[2];sx=PauliMatrix[1];sz=PauliMatrix[3];
Projectors onto the ground and excited state of one atom
In[]:=
proj0={{0},{1}}.Transpose[{{0},{1}}];proj1={{1},{0}}.Transpose[{{1},{0}}];
Driving field Ω and values of the two times
In[]:=
Ω[ε_]:=π(1-ε);T1=1;T2=10;
The two Hamiltonians: for the population transfers and for the interaction.
H1
H
2
In[]:=
H1[ε_]:=Ω[ε]/2KroneckerProduct[sx,id]+Ω[ε]/2KroneckerProduct[id,sx];H2[v_]:=vKroneckerProduct[proj1,proj1];
The evolution operators associated to the Hamiltonians
In[]:=
U1[ε_]:=MatrixExp[-I*T1*H1[ε]];U2[v_]:=MatrixExp[-I*T2*H2[v]];U[ε_,v_]:=U2[v].U1[ε];U[ε,v]//MatrixForm//FullSimplify
Out[]//MatrixForm=
-10v 2 Sin πε 2 | - 1 2 -10v | - 1 2 -10v | - 1 2 -10v |
- 1 2 | 2 Sin πε 2 | - 2 Cos πε 2 | - 1 2 |
- 1 2 | - 2 Cos πε 2 | 2 Sin πε 2 | - 1 2 |
- 2 Cos πε 2 | - 1 2 | - 1 2 | 2 Sin πε 2 |
Now we apply the evolution operator U=U2U1 to the initial state of the system
Now we apply the evolution operator to the initial state of the system
U=
U
2
U
1
We apply U twice, since we want the evolution of the initial state for one period
T=2+2
T
1
T
2
In[]:=
psit[ε_,v_]:=U[ε,v].U[ε,v].psi0;psit[ε,v]//FullSimplify//MatrixForm
Out[]//MatrixForm=
- 1 4 -20v 10v 2 Sin[πε] |
1 4 -5v |
1 4 -5v |
1 16 -2πε 4 (-1+ πε -10v 4 (1+ πε 2 (-1+ 2πε |
Observable which will be used to measure the population of the ground state in the first atom
In[]:=
op1at=KroneckerProduct[proj0,id];op1at//MatrixForm
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 0 | 0 | 1 |
Compute the fidelity for one period
T
In[]:=
fid1at[ε_,v_]:=ConjugateTranspose[psit[ε,v]].op1at.psit[ε,v];fid1at[ε,v]//ComplexExpand//FullSimplify
Out[]=
(5+3Cos[2πε]-2Cos[10v]+2Sin[πε]Sin[2πε])
1
8
2
Sin[πε]
2
Sin[5v]
Expand the fidelity for small ϵ. The result corresponds to the Eq. (11) of our manuscript
In[]:=
Series[fid1at[ϵ,v],{ϵ,0,3}]//ComplexExpand//FullSimplify//TrigReduce
Out[]=
{{1-+}}
2
π
2
Cos[5v]
2
ϵ
4
O[ϵ]
In[]:=
labels=Directive[FontSize20,Black,Italic];ticks={10^-3,10^-4,10^-5,10^-6};
In[]:=
DensityPlot[1-fid1at[ε,v],{ε,-0.015,0.015},{v,-0.5,0.5},PlotLegendsBarLegend[Automatic,Ticksticks],ColorFunctionColorData[{"BlueGreenYellow","Reverse"}],ScalingFunctions{None,None,"Log"},PlotLabel"Infidelity after one period",FrameLabel{ϵ,V},LabelStylelabels,FrameTicks{{-0.01,0,0.01},{-0.4,-0.2,0,0.2,0.4}},PlotPoints100,PlotRange{10^-6,10^-1}]
Out[]=
 | 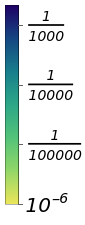 |
Thefigurecorrespondstothefigure3(a)ofourwork=(2m+1)π.
https://arxiv.org/abs/2104.10928
.Itrepresentstheinfidelityforoneperiodinalogarithmicscale,highlightingthesimplebutimportantrelationfortheoptimalvaluesoftheinteractionwhichcompensatethestaticerrorϵ:VT
2
Cite this as: Michele Delvecchio, "Two periodically driven interacting qubits" from the Notebook Archive (2021), https://notebookarchive.org/2021-06-bjbq4hz
Download
