Distributed consensus in Multiway Graph Cellular Automata
Author
Andrés Felipe Bermúdez Mendoza
Title
Distributed consensus in Multiway Graph Cellular Automata
Description
We build a Multiway Graph Cellular Automata which generates non-deterministic evolutions of graph cellular automata and thus be able to analyze the consensus, when it happens through three consensus tracking functions.
Category
Essays, Posts & Presentations
Keywords
Multiway System, Cellular Automaton, Distributed Consensus, Multiway Graph, Majority Rule, non deterministic evolutions
URL
http://www.notebookarchive.org/2021-07-625hkh3/
DOI
https://notebookarchive.org/2021-07-625hkh3
Date Added
2021-07-13
Date Last Modified
2021-07-13
File Size
32.54 megabytes
Supplements
Rights
CC0 1.0
Download
Open in Wolfram Cloud
WOLFRAM SUMMER SCHOOL 2021
Distributed consensus in Multiway Graph Cellular Automata
Distributed consensus in Multiway Graph Cellular Automata
Andrés Felipe Bermúdez Mendoza
National University of Colombia
The objective of this project was to build mutiway graph cellular automatons that evolve asynchronously to reach consensus, using majority rule. Then, using the tracking functions, we extract the information for each mutiway graph cellular automaton, first if it reaches consensus or not, then the complexity and finally the time required to reach consensus. Several experiments were carried out and we find different results were obtained by experimenting with the construction of multiway graphs cell automata. One of them was determined that for a multiway graph cellular automaton the time required to reach consensus varies according to the path because first not all reach consensus and second it evolves asynchronously unlike regular cellular automata where the time required to reaching consensus for either path is the same. It was determined that for future projects it is possible to study the hitting time problem or study possible properties of Multiway Graph Cellular Automaton to obtain good rules that reach consensus and then introduce noise and that finding it is good to resist the effects of noise in the system.
Introduction
Introduction
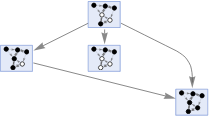
“The problem of distributed consensus” by Stephen Wolfram considers graph cellular automata, where the cells in a cellular automaton can be allowed to be at nodes of a graph. Distributed consensus is a way of describing decentralized verification protocols in networks. Graph cellular automata are useful to understand distributed consensus because they model how information is propagated through a network via local communication of nodes. For a graph, the majority rule for the cellular automaton should allow an arbitrary number of nearest neighbor nodes. A characteristic of regular cellular automata is that all cell values update synchronously across computational steps. For certain graph cellular automaton rules, applying asynchronous updating leads to confluence, which means that regardless of the intermediate states, there is always a convergence in the final result but in some paths, consensus may not be achieved. A multiway graph can be used to record all possible threads in the evolution of a graph cellular automaton. We build a Multiway Graph Cellular Automata which generates non-deterministic evolutions of graph cellular automata and thus be able to analyze the consensus, when it happens through three consensus tracking functions. First, we created the consensus tracking functions for the case of normal cellular automaton for the simple sorting rule where it evolved synchronously observing that all paths to reach right consensus take the same number of steps. Then building the multiway graph cell automata to evolve asynchronously it was observed that the number of steps required per path to reach consensus does not all have the same number, which opens the possibility of determining a distribution to obtain more information from the system. As the next step in this project, once it has been determined that the initial state is worth studying the idea is to find a version of Toom’s rule that reaches consensus and that also works in graphics because it is good at resisting the effects of noise in the system.
Out[]=
Figure 1. Example of 1D deterministic cellular automaton (rule GKL) that achieves successfully “Global consensus”. [1]
Code to build multiway graph cellular automaton
Code to build multiway graph cellular automaton
Normal cellular automaton example
Normal cellular automaton example
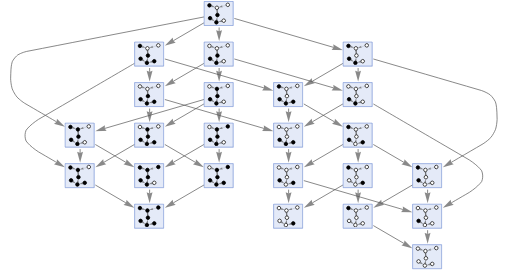
First, we created the consensus tracking functions for the case of normal cellular automaton for the simple sorting rule where it evolved synchronously.
Out[]=
Figure 2. Code for build a Multiway graph cellular automaton for rule 232 used in “The problem of the distributed consensus” by Stephen Wolfram. [1]
Multiway graph cellular automaton
Multiway graph cellular automaton
States
States
To build the initial state we have
In[]:=
points=RandomPointConfiguration[HardcorePointProcess[1,15,2],Rectangle[{0,0},{40,40}]]["Points"]
In[]:=
colors=Table[RandomChoice[{.7,.3}{Black,White}],Length[points]]
In[]:=
init=AssociationThread[pointscolors]
Rules
Rules
Node dependencies are generated
In[]:=
NodeDependencies[points_,nn_,rad_:{1}]:=Table[nDeleteCases[Flatten[Map[Position[points,#]&,VertexOutComponent[NearestNeighborGraph[points,nn,DirectedEdgesTrue,DistanceFunctionEuclideanDistance],points[[n]],rad]]],n],{n,Range[Length[points]]}]
Multiway Graph
Multiway Graph
In[]:=
SynchronousStepNewColors[dependencies_,colors_]:=Flatten[Map[With[{neighbors=Sort[Counts[Part[colors,Last[#]]],Greater]},If[DuplicateFreeQ[Values[neighbors]],First[Keys[neighbors]],colors[[First[#]]]]]&,dependencies]]
In[]:=
getGraphCAEvents[state_,dependencies_]:=With[{changes=Thread[Keys[state]Transpose[{Values[state],SynchronousStepNewColors[dependencies,Values[state]]}]]},Table[{changes[[n]],(First[#]->First[Last[#]])&/@Take[changes,n-1],(First[#]->First[Last[#]])&/@Take[changes,{n+1,-1}]},{n,Length[changes]}]]
In[]:=
applyGraphCAEvent[event:{position_List->{input_,output_},prefix_List,suffix_List}]:=Association[Join[prefix,{position->output},suffix]]
In[]:=
getGraphCASuccessors[state_,dependencies_,updates_]:=Fold[applyGraphCAEvent[getGraphCAEvents[#1,dependencies][[#2]]]&,state,#]&/@Subsets[Range[Length[state]],{updates}]
In[]:=
generateGraphCAMultiway[init_,t_,updates_,nn_,rad_:{1}]:=With[{rules=NodeDependencies[Keys[init],nn,rad]},VertexDelete[SimpleGraph[Flatten[If[ListQ[Last[#]],Table[DirectedEdge[First[#],Last[#][[n]]],{n,Length[Last[#]]}],DirectedEdge@@#]&/@Flatten[NestList[(#->Union[getGraphCASuccessors[#,rules,updates]]&)/@Flatten[Last/@#]&,{<||>->init},t]]],ResourceFunction["WolframPhysicsProjectStyleData"]["StatesGraph","Options"]],<||>]]
In[]:=
ConsensusState[points_,colors_,nn_:5]:=NearestNeighborGraphpoints,nn,DirectedEdgesTrue,DistanceFunctionEuclideanDistance,VertexStyleMapThread[Rule,{points,colors}],VertexSize0.5,EdgeStyleDirectiveThin,
,Arrowheads[Tiny]
In[]:=
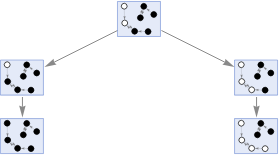
getStateGraphics[state_,nn_,width_]:=Framed[Style[ConsensusState[Keys[state],Values[state],nn],Hue[0.62,1,0.48]],Background->Directive[Opacity[0.2],Hue[0.62,0.45,0.87]],FrameMargins->{{2,2},{0,0}},RoundingRadius->0,FrameStyle->Directive[Opacity[0.5],Hue[0.62,0.52,0.82]]];
In[]:=
getStateRenderingFunction[nn_]:=Inset[getStateGraphics[#2,nn,First[#3]],#1,Center,{First[#3],Automatic}]&;
Out[]=
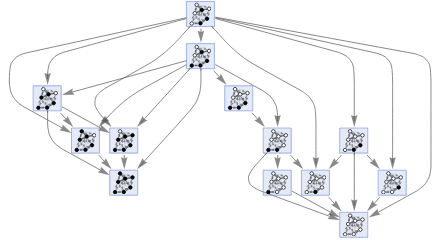
Figure 3. Example for Multiway graph cellular automaton for asynchronous steps.
Code for consensus tracking functions
Code for consensus tracking functions
To analyze multiway systems, three properties are taken, the first the proportion of the colors (Black, White) of the final states, this to observe in the multiway graph cellular automaton whether or not there is consensus, the second to observe the percentage of paths in the multiway system that reach consensus and the third the time required to reach consensus per path, knowing that time is defined as steps.
For Normal cellular automaton
For Normal cellular automaton
◼
Color proportions of the final states of multiway system
In[]:=
calculateFinalColorProportionsSS[multiway_,colors_:{0->White,1->Black}]:=N[Counts[#]/Length[#]]&/@(Apply[List]/@Select[VertexList[multiway],VertexOutDegree[multiway,#]===0&]/.colors)
◼
Percentage of paths in the multiway system that reach consensus (whole multiway system)
In[]:=
calculateSuccessfulPathsSS[multiway_]:=Module[{init=First[Select[VertexList[multiway],VertexInDegree[multiway,#]===0&]],paths},paths=Level[FindPath[multiway,init,#,Infinity,All]&/@Select[VertexList[multiway],VertexOutDegree[multiway,#]===0&],{2}];Length[Select[paths,#[[-1]]===state@@ConstantArray[First[Last[SortBy[Normal[Counts[List@@init]],Last]]],Length[init]]&]]/Length[paths]]
◼
Time to reach consensus for each path in the multiway system
In[]:=
calculateConsensusTimeSS[multiway_]:=With[{init=First[Select[VertexList[multiway],VertexInDegree[multiway,#]===0&]]},Length/@FindPath[multiway,init,state@@ConstantArray[First[Last[SortBy[Normal[Counts[List@@init]],Last]]],Length[init]],Infinity,All]]
For Multiway graph cellular automaton
For Multiway graph cellular automaton
◼
Color proportions of the final states of multiway system
In[]:=
calculateFinalColorProportionsAS[multiway_,colors_:{0->White,1->Black}]:=Counts[#]/Length[#]&/@(Values/@Select[VertexList[multiway],VertexOutDegree[multiway,#]===0&])
◼
Percentage of paths in the multiway system that reach consensus (whole multiway system)
In[]:=
calculateSuccessfulPathsAS[multiway_]:=N[Module[{init=First[Select[VertexList[multiway],VertexInDegree[multiway,#]===0&]],paths},paths=Level[FindPath[multiway,init,#,Infinity,All]&/@Select[VertexList[multiway],VertexOutDegree[multiway,#]===0&],{2}];Length[Select[paths,#[[-1]]===AssociationThread[Keys[init],Table[First[Last[SortBy[Normal[Counts[Values[init]]],Last]]],Length[init]]]&]]/Length[paths]]]
◼
Time to reach consensus for each path in the multiway system
In[]:=
calculateConsensusTimeAS[multiway_]:=Module[{init=First[Select[VertexList[multiway],VertexInDegree[multiway,#]===0&]],final},final=AssociationThread[Keys[init],Table[First[Last[SortBy[Normal[Counts[Values[init]]],Last]]],Length[init]]];If[VertexQ[multiway,final],Length/@FindPath[multiway,init,AssociationThread[Keys[init],Table[First[Last[SortBy[Normal[Counts[Values[init]]],Last]]],Length[init]]],Infinity,All],{}]]
Method
Method
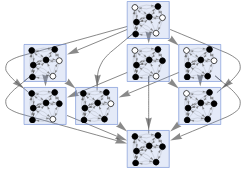
We first construct the initial states of the graph by generating pairs of random points and then associate them with a white or black state. It should be shown that there is a tendency to avoid “bridges” where colors can be balanced on “all sides” of a particular node, in addition to the fact that the lack of symmetry inhibits the appearance of cycles. For this, node dependencies are generated, which depend on the nearest neighbors where the majority rule works better [1] and also depends on the radius that for all cases of experimentation we take as 1. Using the corresponding functions we obtain the multiway graph cellular automaton, and then analyze the system with the consensus tracking functions. With them using “InteractiveListSelector” we select the consensus cases and obtain conclusions about the systems obtained. It is experienced for the following cases:
◼
Changing the amount of nearest neighborhoods with constant Asynchronous Updates
◼
Changing the amount of Asynchronous Updates with constant nearest neighbors
◼
Changing the percentages of the majority rule with constant nearest neighbors and constant asynchronous updates
◼
Random Examples
Experimentation
Experimentation
Setting a certain number of points, which should stay the same all through the analysis
In[]:=
points=Table[RandomPointConfiguration[HardcorePointProcess[1,15,2],Rectangle[{0,0},{40,40}]]["Points"],20]
Note that to reproduce the examples it is necessary to select the cases where consensus is reached when using the “InteractiveListSelector” function.
Changing the amount of nearest neighborhoods with constant Asynchronous Updates = 2
Changing the amount of nearest neighborhoods with constant Asynchronous Updates = 2
Generating consensus results for 70% initial black majority with 2 asynchronous updates and 1 nearest neighbors at radius 1.
Out[]=
Out[]=
,
,
,
,
,
,
,
,
,
,
,
Generating consensus results for 70% initial black majority with 2 asynchronous updates and 2 nearest neighbors at radius 1.
Out[]=
,,,,,,,,,,,,,,,,,,,
1,
1,0.568627,{3,3,4,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,5,5,5,6,6,6,6,6}
Add
1,1.,{2}
Add
,,,,0.,{}
2
7
5
7
4
7
3
7
Add
,,,,,,,,1,0.617021,{3,3,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,5,5,5}
3
4
1
4
1
2
1
2
5
8
3
8
3
8
5
8
Add
1,1.,{2}
Add
,,,,1,0.74359,{3,3,4,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,5,5,5,6,6,6,6,6}
4
7
3
7
3
7
4
7
Add
1,1.,{2}
Add
1,1.,{3,3,3,3,3,3,4,4,4,4,4,4}
Add
1,1.,{2}
Add
1,1.,{2}
Add
,,0.,{}
5
7
2
7
Add
1,,,0.666667,{2,3}
1
2
1
2
Add
1,,,0.75,{2,3,3}
2
3
1
3
Add
1,1.,{2,3,3}
Add
1,1.,{4}
Add
1,1.,{2}
Add
1,,,0.6,{2,3,3}
1
3
2
3
Add
,,0.,{}
1
4
3
4
Add
1,1.,{2,3,3}
Add
,,,,0.,{}
5
7
2
7
4
7
3
7
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
Generating consensus results for 70% initial black majority with 2 asynchronous updates and 3 nearest neighbors at radius 1.
Out[]=
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Generating consensus results for 70% initial black majority with 2 asynchronous updates and 4 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
1,1.,{3,3,3,3,3,4,4,4,4}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{3,3,3,3,3,3,4,4,4,4,4,4}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
{}
Add
1,1.,{2}
Add
{}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{3,3,3,3,3,3,4,4,4,4,4,4}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
,,1,1,0.177419,{3,4,4,4,4,4,4,5,5,5,5}
1
2
1
2
Add
1,1.,{2}
Add
1,1.,{3,3,3,3,4,4,4,4}
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Changing the amount of Asynchronous Updates with constant nearest neighbors nn=2
Changing the amount of Asynchronous Updates with constant nearest neighbors nn=2
Generating consensus results for 70% initial black majority with 1 asynchronous updates and 2 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
1,1.,{3,3}
Add
,,1,,,,,0.428571,{4,4,4,4,4,4}
5
8
3
8
1
4
3
4
1
2
1
2
Add
1,1.,{2}
Add
,,0.,{}
5
8
3
8
Add
1,,,0.5,{3}
2
3
1
3
Add
1,,,,,0.5,{3,3}
5
7
2
7
4
7
3
7
Add
1,0.,{}
Add
1,1.,{4,4}
Add
1,1.,{2}
Add
{}
Add
1,1.,{2}
Add
,,0.,{}
1
2
1
2
Add
{}
Add
1,1.,{3,3}
Add
1,1.,{2}
Add
1,1.,{2}
Add
{}
Add
,,0.,{}
1
4
3
4
Add
1,1.,{2}
Add
1,1.,{2}
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
,
Generating consensus results for 70% initial black majority with 2 asynchronous updates and 2 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
1,1.,{2}
Add
,,0.,{}
3
8
5
8
Add
1,,,0.6,{2,3,3}
4
7
3
7
Add
,,,,0.,{}
3
4
1
4
5
8
3
8
Add
1,1.,{2}
Add
,,,,0.,{}
4
7
3
7
3
7
4
7
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
{}
Add
,,0.,{}
2
7
5
7
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
{}
Add
1,,,,,0.25,{3,4}
5
7
2
7
3
7
4
7
Add
,,1,1,0.411765,{3,3,3,3,4,4,4}
1
2
1
2
Add
,,0.,{}
1
3
2
3
Add
,,1,0.7,{3,3,3,3,4,4,4}
5
8
3
8
Add
1,0.,{}
Add
{}
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
,
,
,
,
,
,
Generating consensus results for 70% initial black majority with 3 asynchronous updates and 2 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
{}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
{}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
,,0.,{}
4
7
3
7
Add
,,1,0.6,{2,3,3}
5
7
2
7
Add
,,1,0.5,{3}
4
7
3
7
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
1,1.,{2}
Add
,,,,1,0.5,{3,3,4,4,4}
4
7
3
7
2
7
5
7
Add
,,0.,{}
5
7
2
7
Add
{}
Add
1,,,0.6,{2,3,3}
1
3
2
3
Add
1,,,0.75,{2,3,3}
5
8
3
8
Add
1,1.,{2}
Add
{}
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
,
,
,
,
,
,
Generating consensus results for 70% initial black majority with 4 asynchronous updates and 2 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
1,1.,{2,3,3}
Add
1,1.,{2,3,3,3,3,3,3,4,4,4,4,4,4}
Add
,,,,,,0.,{}
5
7
2
7
4
7
3
7
5
7
2
7
Add
,,0.,{}
1
4
3
4
Add
1,,,1,0.125,{3}
2
3
1
3
Add
1,1.,{2}
Add
1,1.,{2}
Add
{}
Add
1,1.,{2}
Add
1,1.,{2,3}
Add
{}
Add
1,1.,{2,3,3,3,3,3,3,4,4,4,4,4,4}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
{}
Add
1,1.,{2,3,3}
Add
{}
Add
{}
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
,
,
,
,
,
,
Changing the percentages of the majority rule with constant nearest neighbors and constant asynchronous updates at radius 1
Changing the percentages of the majority rule with constant nearest neighbors and constant asynchronous updates at radius 1
Generating consensus results for 10% initial black majority with 3 asynchronous updates and 4 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
{}
Add
{}
Add
{}
Add
1,1.,{2}
Add
{}
Add
{}
Add
{}
Add
1,1.,{2}
Add
,,1,0.875,{3,3,3,4,4,4,4}
4
7
3
7
Add
{}
Add
{}
Add
{}
Add
1,1.,{2}
Add
1,1.,{2}
Add
,,1,1,0.266667,{3,3,4,4}
4
7
3
7
Add
{}
Add
{}
Add
1,1.,{2}
Add
{}
Add
{}
Add
Clear |
Copy |
Out[]=
Generating consensus results for 20% initial black majority with 3 asynchronous updates and 4 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
1,1.,{2,3,3,3,3,3,3,4,4,4,4,4,4}
Add
1,1.,{2}
Add
1,1.,{2}
Add
,,1,0.8,{4,4,5,5}
5
8
3
8
Add
{}
Add
1,1.,{2}
Add
{}
Add
1,1.,{2}
Add
1,1,,,0.0384615,{3,4,4}
3
7
4
7
Add
{}
Add
{}
Add
{}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
Clear |
Copy |
Out[]=
Generating consensus results for 30% initial black majority with 3 asynchronous updates and 4 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1,0.521739,{2,3,3,3,4,4,4,5,5,5,6,6}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3,3,3,4,4,4,4}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1,0.342857,{3,3,4,4,4,4,5,5,5,5,6,6}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
{}
Add
1,1.,{2}
Add
1,1.,{2}
Add
Clear |
Copy |
Out[]=
,
,
Generating consensus results for 40% initial black majority with 3 asynchronous updates and 4 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
1,1.,{2,3,3}
Add
1,1.,{2,3,3,3,3,3,3,4,4,4,4,4,4}
Add
1,1.,{2,3,3}
Add
,,1,1,0.148148,{3,3,4,4,4,4,5,5}
1
2
1
2
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3,3,3,3,4,4,4,4}
Add
1,1,0.264706,{2,3,3,3,3,4,4,4,4}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1,0.5,{3,4,4}
Add
,,1,1,0.808824,{3,3,3,3,3,3,3,3,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5}
1
2
1
2
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3,3,3,3,4,4,4,4}
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
Generating consensus results for 50% initial black majority with 3 asynchronous updates and 4 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
1,1.,{2,3,3}
Add
1,1,0.688889,{2,3,3,3,3,3,3,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,6,6,6,6,6,6}
Add
1,1.,{2}
Add
,,1,0.8,{4,4,5,5}
5
8
3
8
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3,3,3,4,4,4,4}
Add
1,1,0.625,{2,3,3,3,3,3,4,4,4,4}
Add
1,1.,{2}
Add
1,0.,{}
Add
,,1,1,0.266667,{3,3,4,4}
4
7
3
7
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3,3,3,3,3,4,4,4,4,4,4}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
,
,
,
,
,
Generating consensus results for 60% initial black majority with 3 asynchronous updates and 4 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
1,1,0.619048,{2,3,3,3,3,3,3,4,4,4,4,4,4}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3,3,3,3,3,4,4,4,4,4,4}
Add
,,1,0.875,{3,3,3,4,4,4,4}
1
2
1
2
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
1,1.,{2,3,3,3,3,3,3,4,4,4,4,4,4}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3,3,3,3,3,4,4,4,4,4,4}
Add
,,1,1,0.16,{3,3,4,4}
4
7
3
7
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
,,1,,,,,1,,,0.0909091,{3,3,3,4,4,4,4}
3
8
5
8
5
8
3
8
1
2
1
2
1
2
1
2
Add
{}
Add
1,1.,{2}
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Generating consensus results for 70% initial black majority with 3 asynchronous updates and 4 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
1,1,0.619048,{2,3,3,3,3,3,3,4,4,4,4,4,4}
Add
1,1.,{2,3,3}
Add
1,,,0.866667,{2,3,3,3,3,3,3,4,4,4,4,4,4}
4
7
3
7
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3}
Add
{}
Add
1,1.,{2}
Add
1,,,0.818182,{2,3,3,3,3,4,4,4,4}
4
7
3
7
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1,0.764706,{2,3,3,3,3,3,3,4,4,4,4,4,4}
Add
1,1.,{2}
Add
1,0.,{}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
{}
Add
1,1.,{2}
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Generating consensus results for 80% initial black majority with 3 asynchronous updates and 4 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
{}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
1,,,1,0.325,{2,3,3,3,3,3,3,4,4,4,4,4,4}
4
7
3
7
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,,,1,0.342857,{3,3,4,4,4,4,5,5,5,5,6,6}
3
7
4
7
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
1,0.,{}
Add
{}
Add
1,1.,{2,3,3}
Add
{}
Add
{}
Add
{}
Add
1,1.,{2,3,3}
Add
1,1.,{2,3,3,3,3,3,4,4,4,4}
Add
{}
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
Generating consensus results for 90% initial black majority with 3 asynchronous updates and 4 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
1,1.,{2}
Add
1,1.,{2,3,3}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{2}
Add
{}
Add
{}
Add
1,1.,{2,3,3}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{2}
Add
1,1.,{2}
Add
{}
Add
Clear |
Copy |
Out[]=
,
,
,
,
,
,
,
,
,
Random Examples
Random Examples
Generating consensus results for 70% initial black majority with 1 asynchronous updates and 1 nearest neighbors at radius 1
Out[]=
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
Generating consensus results for 70% initial black majority with 7 asynchronous updates and 7 nearest neighbors at radius 1
Out[]=
,,,,,,,,,,,,,,,,,,,
{}
Add
1,1.,{2}
Add
{}
Add
1,1.,{2}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
{}
Add
1,1.,{2}
Add
{}
Add
{}
Add
Clear |
Copy |
Out[]=
,
Results and Concluding remarks
Results and Concluding remarks
The first thing that can be observed is that the time to reach consensus in multiway graph cellular automatons that evolve asynchronously are not the same for all paths, unlike normal cellular automata when they evolve synchronously. This is important for a future project, since it is possible to obtain probabilistic distributions of the time in reaching consensus for different paths in a system, allowing to open a hitting time problem. It can be seen that when the nearest neighbors are greater than 4, the complexity of the multiway graph cellular automata decreases. When the values of the nearest neighbors are increased a lot, it is more difficult to produce multiway graphs cellular automata and the complexity decreases considerably, therefore the time to find the consensus is much less than using small values for the nearest neighbors and the asynchronous updates. Finally, by varying the majority rule for the construction of multiway graphs cellular automata, where it is observed that the greater the probability of obtaining the black color, the greater cases of consensus are obtained.
Distributed consensus is a way of describing decentralized verification protocols in networks, for example cryptocurrencies or security databases. For this reason, it is worthwhile to continue studying possible properties of Multiway Graph Cellular Automaton to obtain a Toom’s rule that reach consensus and then experiment with the resistance of the effects of noise in the system. Another interesting problem is the hitting time which is the expected value of time in a random path given an initial state. For this reason, it would be important to see the distributions that are obtained with the “calculateConsensusTimeAS” function.
Distributed consensus is a way of describing decentralized verification protocols in networks, for example cryptocurrencies or security databases. For this reason, it is worthwhile to continue studying possible properties of Multiway Graph Cellular Automaton to obtain a Toom’s rule that reach consensus and then experiment with the resistance of the effects of noise in the system. Another interesting problem is the hitting time which is the expected value of time in a random path given an initial state. For this reason, it would be important to see the distributions that are obtained with the “calculateConsensusTimeAS” function.
Keywords
Keywords
◼
Multiway System
◼
Cellular Automaton
◼
Distributed Consensus
◼
Multiway Graph
◼
Majority Rule
◼
non-deterministic evolutions
Acknowledgment
Acknowledgment
Thanks to my mentor Mano Namuduri, for accompanying me and guiding me throughout Wolfram Summer School 2021, since without her my project would not have been possible, she gave me the opportunity to learn a lot in each live code session, I really appreciate everything I learned from her. Thanks also to Tobías Canavesi for giving me ideas for consensus tracking features. Thank you Stephen Wolfram for bringing me this project and the entire team for the best opportunity I have ever had in my life so far to attend the Fundamental Physics track. Finally, thanks to all the organizers of the Wolfram Summer School for making this an unforgettable experience.
References
References
◼
[1] Wolfram, S. (2021, May 17). The Problem of Distributed Consensus. https://writings.stephenwolfram.com/2021/05/the-problem-of-distributed-consensus/
◼
[2] Wolfram, S. (2002) A New Kind of Science. Wolfram Media. https://www.wolframscience.com/nks/
◼
[3] WolframResearch.Mathematica. (2021) https://www.wolfram.com/mathematica/
◼
[4] Wolfram, S. (2020, June 19) A Project to Find the Fundamental Theory of Physics. ISBN: 978-1-57955-031-8. https://www.wolfram-media.com/products/a-project-to-find-the-fundamental-theory-of-physics.html
◼
[5] Coulouris, George; Jean Dollimore; Tim Kindberg (2001), Distributed Systems: Concepts and Design (3rd Edition), Addison-Wesley, p. 452, ISBN 978-0201-61918-8
◼
[6] Toom, Andrei (1980). “Stable and attractive trajectories in multicomponent systems”. Multicomponent Random Systems: 549–575
◼
[7] Tanenbaum, Andrew S.; Steen, Maarten van (2002). Distributed systems: principles and paradigms. Upper Saddle River, NJ: Pearson Prentice Hall. ISBN 0-13-088893-1.
◼
[9] Don Tapscott & Alex Tapscott (2016). Deusto. La revolución del Blockchain.
◼
[10] Baxter, Rodney J. (1982), Exactly solved models in statistical mechanics, London: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], ISBN 978-0-12-083180-7, MR 0690578
Cite this as: Andrés Felipe Bermúdez Mendoza, "Distributed consensus in Multiway Graph Cellular Automata" from the Notebook Archive (2021), https://notebookarchive.org/2021-07-625hkh3
Download
