Computing Order Series/Ehrhart Polynomials of Posets with Mathematica
Author
Eric Dolores Cuenca, Jose L. Mendoza-Cortes
Title
Computing Order Series/Ehrhart Polynomials of Posets with Mathematica
Description
We explain how to use Mathematica to compute power series that are important in combinatorics.
Category
Essays, Posts & Presentations
Keywords
combinatorics, power series, generating functions, Ehrhart theory, Stanley order polynomials, operad, series parallel, poset
URL
http://www.notebookarchive.org/2022-02-3pvm73a/
DOI
https://notebookarchive.org/2022-02-3pvm73a
Date Added
2022-02-08
Date Last Modified
2022-02-08
File Size
154.28 kilobytes
Supplements
Rights
CC BY 4.0

Computing Order Series/Ehrhart polynomials of posets with Mathematica
Computing Order Series/Ehrhart polynomials of posets with Mathematica
Eric Dolores Cuenca, Jose L. Mendoza-Cortes
Department of Mathematics, Yonsei University, Seoul, South Korea.
1
2
1
2
Update April 6 2023
Introduction
Introduction
We consider finite partially ordered set (posets). Given a poset, how many ways can we put labels on the vertices using numbers from 1 to and preserving the order?
For example, if the poset is just a union of two points, the label of the first point can be any number between 1 and. Independently of the choice of the first label, the label of the second point is any number between 1 and . In total we have choices.
Now, if the poset is, the first point can have any label between 1 and , and the second point can have any label between the label of plus one and . We use this idea to count the number of ways to label a general poset using Mathematica.
In the paper [1], we review rules to answer this question in the case of Series Parallel posets [2]. This note is mean to explain how to compute the missing case, when the poset is not a series parallel poset.
n
For example, if the poset is just a union of two points, the label of the first point can be any number between 1 and
n
n
2
n
Now, if the poset is
x<y
n-1
x
n
In the paper [1], we review rules to answer this question in the case of Series Parallel posets [2]. This note is mean to explain how to compute the missing case, when the poset is not a series parallel poset.
Code.
Code.
We draw Hasse diagrams [3] from left to right. So, the vertex are the points in the poset, and there is a edge from left to right from a point to it’s successor. Then a line with 9 points corresponds to .
{a<b<c<d<e<f<g<h<i}
In[]:=
myline=
Out[]=

What is the number of order preserving labelings of this line with numbers from 1 to ?
n
We choose a label for between 1 and , the reason is that implies that cannot be , or .
a
n-8
{a<b<c<d<e<f<g<h<i}
a
n
n-1,...n-7
We choose a label for between and , the reason is whatever value has, can be at least and cannot be , or .
We are computing the sum:
b
a+1
n-7
a
b
a+1
n
n-1,...n-6
We are computing the sum:
Out[]=
n-8
∑
a=1
n-7
∑
ba+1
n-6
∑
cb+1
n-5
∑
dc+1
n-4
∑
ed+1
n-3
∑
fe+1
n-2
∑
ge+1
n-1
∑
hg+1
n
∑
ih+1
each term assign a value to the letters . In Mathematica [4] this is equivalent to:
a,b,c,d,e,f,g,h,i
In[]:=
Sum[1,{a,1,n-8},{b,a+1,n-7},{c,b+1,n-6},{d,c+1,n-5},{e,d+1,n-4},{f,e+1,n-3},{g,f+1,n-2},{h,g+1,n-1},{i,h+1,n}]
Out[]=
40320n-109584+118124-67284+22449-4536+546-36+
2
n
3
n
4
n
5
n
6
n
7
n
8
n
9
n
362880
In[]:=
FullSimplify
40320n-109584+118124-67284+22449-4536+546-36+
2
n
3
n
4
n
5
n
6
n
7
n
8
n
9
n
362880
Out[]=
(-8+n)(-7+n)(-6+n)(-5+n)(-4+n)(-3+n)(-2+n)(-1+n)n
362880
(-8+n)(-7+n)(-6+n)(-5+n)(-4+n)(-3+n)(-2+n)(-1+n)n
362880
n |
9 |
We didn’t need Mathematica to find this value, but we follow the same pattern for other posets.
Obtainingtheorderpolynomial
In[]:=
myotherline=

Out[]=
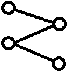
Let’s now compute the number of labelings for the poset using numbers from 1 to :
{a<b>c<d}
n
We need to find a label for those points in the handle, fix a value for between 1 and . Then can have values: , and can have values . Finally, can have values .
Then the expression
a
n-1
b
a+1,...,n
c
1,⋯,b-1
d
c+1,⋯,n
Then the expression
Out[]=
n-1
∑
a=1
n
∑
ba+1
b-1
∑
c=1
n
∑
dc+1
Counts all possible labelings of this new figure, in Mathematica this is equivalent to:
In[]:=
Sum[1,{a,1,n-1},{b,a+1,n},{c,1,b-1},{d,c+1,n}]
Out[]=
1
24
2
n
3
n
4
n
This is Stanley’s strict Order polynomial [5] of
This is Stanley’s strict Order polynomial [5] of
Out[]=

Obtaining the order series
Obtaining the order series
At the end of this notes, we describe how by working with the generating function of order polynomials, we perceive symmetries that are hidden on the polynomials. Those generating functions are called order series [1].In this subsection we show three methods to compute the order series of non Series-Parallel posets from the order polynomial.First method:Theorem: The binomial coefficients are a basis for Stanley order polynomials with integer coefficients. See [6]. We then look for the vectors of (-2n+7-10+5), obtaining . This is the coefficient at degree of the order series. Then the order series is .Second method:Assuming we don’t know the previous theorem, we can ask Mathematica to compute Sum[(-2n+7-10+5),{n,1,Infinity}], and then we write it in terms of . Here, we use the fact that
.Third method:Consider the previous example, we want a differential operator defined on power series, that restricted to returns . Let
1
24
2
n
3
n
4
n
5
+5
+
n |
4 |
n |
3 |
n |
2 |
n
5+5+
4
x
5
(1-x)
3
x
4
(1-x)
2
x
3
(1-x)
1
24
2
n
3
n
4
n
n
x
i
x
i+1
(1-x)
i∈N
i
x
i+1
(1-x)
∞
∑
ni
n |
i |
n
x
SP
n
x
-2n+7-10+5
2
n
3
n
4
n
24
n
x
In[]:=
f[x_]:=1/(1-x)
Then the order series for the poset should be computed by .To find the differential operator, consider the numerator of as a polynomial on : If there is a constant, the operator acted by multiplication on . The linear term on the variable is the result of the action of the operator via because =. Now replace by , etc.The differential operator of the previous example is +, and evaluated on should return the order series of  :
:
a<b>c<d
SP(f(x))
-2n+7-10+5
2
n
3
n
4
n
24
n
f(x)
n
x
d
dx
x
d
dx
a
n
x
na
n
x
2
n
x
d
dx
x
d
dx
-2+7-10
x
d
dx
xx
d
dx
d
dx
xxx
d
dx
d
dx
d
dx
524
xxxx
d
dx
d
dx
d
dx
d
dx
1
1-x

In[]:=
(-2*x*D[ f(x),x]+7x*D[x*D[ f(x),x],x] -10*x*D[x*D[x*D[ f(x),x],x],x] +5*x*D[x*D[x*D[x*D[ f(x),x],x],x],x] )/24 | |
(-2*x*D[f[x],x]+7*x*D[x*D[f[x],x],x]-10*x*D[x*D[x*D[f[x],x],x],x]+5*x*D[x*D[x*D[x*D[f[x],x],x],x],x])/24 | |
Out[]=
1
24
2x
2
(1-x)
1
2
(1-x)
2x
3
(1-x)
1
2
(1-x)
2x
3
(1-x)
4
3
(1-x)
6x
4
(1-x)
1
2
(1-x)
2x
3
(1-x)
4
3
(1-x)
6x
4
(1-x)
8
3
(1-x)
12x
4
(1-x)
18
4
(1-x)
24x
5
(1-x)
In[]:=
Simplify[%5]
Out[]=
-(1+3x+)
2
x
2
x
5
(-1+x)
This is the order series of
In[]:=
myotherline
Out[]=

The series parallel case
Here we explain rules to study the order series of series-parallel posets. Consider the operations on posets: disjoint union of posets and concatenation of posets . Following [1] The order series of an chain is . If we know the order series of and , then the order series of is . Every series parallel poset has an order series of the form with non negative and only a finite number of non zero. The disjoint union is better described in terms of chains, the disjoint union of chains and corresponds to the order series . The operations act linearly on the basis .The advantage of this rules, is that if we know how to write a poset in terms of concatenation and disjoint union, we can apply the previous operations. For example, the poset corresponds to , and we compute .A more interesting example returns . What is the order polynomial of the poset? we replace every instance of by to obtain . This is number of ways to label the poset using numbers from 1 to . We also obtain information about a triangulation of the polytope of the poset.Lemma (Inclusion exclusion): If then the order polytope of is union of copies of simplex and those copies intersect in copies of simplex, and so on. It follows from [6] by using the definition of the canonical triangulation of the order polytope. There is an operad [7] structure of finite posets, it induces operations on Stanley’s order polynomials. We want an explicit description of those operations, for example what is the action on power series of . Feel free to contact me if you are interested on this topics. Order series, Ehrhart series and Hilbert series.To any poset with points, you can associate the order polytope [5]. For polytopes, the Ehrhart series [5] is an important object of study. The order series of a poset is related to the Ehrhart series of the order polytope via .It is also interesting to mention that to the fan of the order polytope, you can associate a toric variety [8]. And for toric varieties there are generating functions called the Hilbert series that coincide with the Ehrhart series.This notebook is the result of work with Anh Nguyen, Amanda Yitong Zou and Antonio Arciniega Nevarez [9] to compute the table below
returns . What is the order polynomial of the poset? we replace every instance of by to obtain . This is number of ways to label the poset using numbers from 1 to . We also obtain information about a triangulation of the polytope of the poset.Lemma (Inclusion exclusion): If then the order polytope of is union of copies of simplex and those copies intersect in copies of simplex, and so on. It follows from [6] by using the definition of the canonical triangulation of the order polytope. There is an operad [7] structure of finite posets, it induces operations on Stanley’s order polynomials. We want an explicit description of those operations, for example what is the action on power series of . Feel free to contact me if you are interested on this topics. Order series, Ehrhart series and Hilbert series.To any poset with points, you can associate the order polytope [5]. For polytopes, the Ehrhart series [5] is an important object of study. The order series of a poset is related to the Ehrhart series of the order polytope via .It is also interesting to mention that to the fan of the order polytope, you can associate a toric variety [8]. And for toric varieties there are generating functions called the Hilbert series that coincide with the Ehrhart series.This notebook is the result of work with Anh Nguyen, Amanda Yitong Zou and Antonio Arciniega Nevarez [9] to compute the table below as well as the results of discussions with Luke Van Popering, Nathan Crock, and Gordon Erlebacher. Our original goal was to understand certain neurons as Non linear signal-flow graphs using the cellular automata 192, you can learn the story here: [10]. The author received funding from the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No . 2020R1C1C1A01008261) . References.
as well as the results of discussions with Luke Van Popering, Nathan Crock, and Gordon Erlebacher. Our original goal was to understand certain neurons as Non linear signal-flow graphs using the cellular automata 192, you can learn the story here: [10]. The author received funding from the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No . 2020R1C1C1A01008261) . References.

t-1

1 J.A. Arciniega-Nevárez, M. Berghoff, E.R. Dolores-Cuenca. An algebra over the operad of posets and structural binomial identities. Bol. Soc. Mat. Mex. 29, 8 (2023). https://doi.org/10.1007/s40590-022-00478-9
2 https://en.wikipedia.org/wiki/Series-parallel_partial_order
3 https://mathworld.wolfram.com/HasseDiagram.html
4 Wolfram Research, Inc., Mathematica, Version 13.0.0, Champaign, IL (2021).
5 M. Beck and R. Sanyal. Combinatorial Reciprocity Theorems: An Invitation to Enumerative Geo-metric Combinatorics, vol. 195, American Mathematical Society, Providence, Rhode Island, first ed. 2018.
6 R. P. Stanley. Combinatorial reciprocity theorems. Adv. Math., 14:194–253, 1974.
7 J.-L. Loday and B. Vallette. Algebraic Operads, Springer-Verlag Berlin Heidelberg, 1st ed., 2012.
8 V. I. Danilov. The geometry of toric varieties, Russian Mathematical Surveys, 33 (1978), pp. 97–154
9 E. Dolores-Cuenca. J. Arciniega-Nevarez, A. Nguyen, A. Zou, L. Van Popering, N. Crock, G. Erlebacher, J. Mendoza-Cortes. Polychrony as Chinampas. Algorithms 2023, 16(4), 193; https://doi.org/10.3390/a16040193
10 E. Dolores-Cuenca. New Identities in Combinatorics Discovered with Help from Mathematica Software. Wolfram Technology Conference 2021 https://www.wolfram.com/broadcast/video.php?v=3593
2 https://en.wikipedia.org/wiki/Series-parallel_partial_order
3 https://mathworld.wolfram.com/HasseDiagram.html
4 Wolfram Research, Inc., Mathematica, Version 13.0.0, Champaign, IL (2021).
5 M. Beck and R. Sanyal. Combinatorial Reciprocity Theorems: An Invitation to Enumerative Geo-metric Combinatorics, vol. 195, American Mathematical Society, Providence, Rhode Island, first ed. 2018.
6 R. P. Stanley. Combinatorial reciprocity theorems. Adv. Math., 14:194–253, 1974.
7 J.-L. Loday and B. Vallette. Algebraic Operads, Springer-Verlag Berlin Heidelberg, 1st ed., 2012.
8 V. I. Danilov. The geometry of toric varieties, Russian Mathematical Surveys, 33 (1978), pp. 97–154
9 E. Dolores-Cuenca. J. Arciniega-Nevarez, A. Nguyen, A. Zou, L. Van Popering, N. Crock, G. Erlebacher, J. Mendoza-Cortes. Polychrony as Chinampas. Algorithms 2023, 16(4), 193; https://doi.org/10.3390/a16040193
10 E. Dolores-Cuenca. New Identities in Combinatorics Discovered with Help from Mathematica Software. Wolfram Technology Conference 2021 https://www.wolfram.com/broadcast/video.php?v=3593
Cite this as: Eric Dolores Cuenca, Jose L. Mendoza-Cortes, "Computing Order Series/Ehrhart Polynomials of Posets with Mathematica" from the Notebook Archive (2022), https://notebookarchive.org/2022-02-3pvm73a
Download
