The Parabola: Parametric Equations

Tomas Garza

Description

“One description of a parabola involves a point (the focus) and a line (the directrix). The focus does not lie on the directrix. The parabola is the locus of points in a plane that are equidistant from both the directrix and the focus”. The previous sentences are taken from Wikipedia, in the entry parabola, which contains a very thorough study of the subject. Yet, it deals only with Cartesian and polar coordinates, and I think it might be interesting to draw the curve defined by the above conditions using parametric equations.

Parametric equations for the parabola

I will begin by finding such equations using purely geometric reasoning.

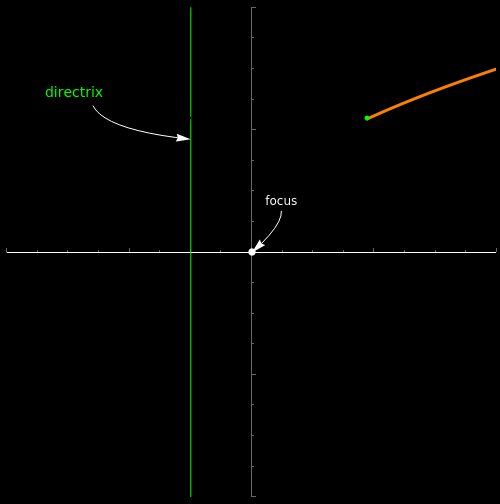
Thus, given the focus (located at the origin of coordinates) and the directrix (the green line perpendicular to the axis) at a distance a from it, we wish to find the locus of the points equidistant from the focus and the directrix. In the figure below, I have drawn a line from the focus, at an arbitrary angle θ with the horizontal axis (in orange, in the figure). This line (in white) intersects the directrix at a point A, from which I draw a line (in red) perpendicular to the directrix .

On the other hand, a line (in green) is drawn from the focus, which intersects the red line at a point V, with the condition that the length of the segment from the focus to V is equal to the distance from A to V. To achieve this we must finding the angle between the horizontal axis and the green segment.

In the interactive figure below the procedure is outlined. We use the angle colors in the derivation of the solution, which makes it easier to follow it. The description of the content appears there, and the reader may go forward or backward using the sequence button. The angle, θ, may be changed with the sliding control in order to observe different positions of V. In step 3 the parametric equations are shown. The code may be seen by double-clicking the outer bracket of the figure below.

Out[]=

sequence

angle θ

Drawing the parabola

Once the parametric equations are available, the curve may be drawn as a function of angle θ, as may be seen in the image below. Assume the position of the focus (at the origin of coordinates) and the directrix, at a distance a from the focus. This may be changed using the slider control, and the development of the curve can be observed moving the angle θ. A constructive view is available clicking the corresponding button; this gives access to the elements used in the construction of the graphic. The code may be seen by double-clicking the outer bracket of the figure below.

Out[]=

1 simple view

2 constructive view

position of

the directrix

Cite this as: Tomas Garza, "The Parabola: Parametric Equations" from the Notebook Archive (2023), https://notebookarchive.org/2023-03-a72mnic