The Dirac equation as a linear tensor equation for one component
Author
Andrey Akhmeteli
Title
The Dirac equation as a linear tensor equation for one component
Description
Supplementary material to https://arxiv.org/abs/2312.10058
Category
Academic Articles & Supplements
Keywords
URL
http://www.notebookarchive.org/2024-03-2sq7ma9/
DOI
https://notebookarchive.org/2024-03-2sq7ma9
Date Added
2024-03-06
Date Last Modified
2024-03-06
File Size
3.04 megabytes
Supplements
Rights
Redistribution rights reserved

The Dirac equation as a linear tensor equation for one component
The Dirac equation as a linear tensor equation for one component
(*Thisnotebookisanancillaryfileandcontainssupplementarymaterialforthearticle"The Dirac equation as a linear tensor equation for one component"byAndreyAkhmeteli(
https://arxiv.org/abs/2312.10058
).IfyoudonothaveaccesstoMathematica,youcaninspectthisnotebookhere,atNotebookArchive,toseeproofsofsomestatementsinthearticle,orviewthenotebookusingthefree-of-chargeWolframPlayer.IfyouhaveaccesstoMathematica,pleasenotethatthisnotebookconsistsof10fragments,whichshouldbeevaluatedinsuccession.Evaluationofeachofthemtakesnomorethan2minutesontheauthor'sdesktop.Mathematicaversionis11.3.0.0.Shortcommentsareprovidedattheendoftheoutputofeachfragment.*)a={{a11,a12},{a21,a22}};MatrixForm[a]"a"ah=ConjugateTranspose[a];MatrixForm[ah]"ah"z2={{0,0},{0,0}};MatrixForm[z2]"z2"s1={{0,1},{1,0}};MatrixForm[s1]s2={{0,-I},{I,0}};MatrixForm[s2]s3={{1,0},{0,-1}};MatrixForm[s3]"s1-3"iun2={{1,0},{0,1}};MatrixForm[iun2]"iun2"taut=Array[z2&,4];taut[[1]]=-iun2;taut[[2]]=s1;taut[[3]]=s2;taut[[4]]=s3;rhot=Array[z2&,4];rhot[[1]]=-iun2;rhot[[2]]=-s1;rhot[[3]]=-s2;rhot[[4]]=-s3;taub=Array[z2&,4];taub[[1]]=-iun2;taub[[2]]=-s1;taub[[3]]=-s2;taub[[4]]=-s3;lor=Array[0&,{4,4}];For[i=1,i≤4,i++,For[j=1,j≤4,j++,lor[[i,j]]=FullSimplify[(1/2)Tr[rhot[[i]].a.taub[[j]].ah]]];];MatrixForm[lor]"lor"mat1={{a11,a12,a21,a22},{a21,a22,a11,a12},{-Ia21,-Ia22,Ia11,Ia12},{a11,a12,-a21,-a22}};MatrixForm[mat1]"mat1"mat2={{Conjugate[a11],Conjugate[a12],-IConjugate[a12],Conjugate[a11]},{Conjugate[a12],Conjugate[a11],IConjugate[a11],-Conjugate[a12]},{Conjugate[a21],Conjugate[a22],-IConjugate[a22],Conjugate[a21]},{Conjugate[a22],Conjugate[a21],IConjugate[a21],-Conjugate[a22]}};MatrixForm[mat2]"mat2"mat3=mat1.mat2/2;MatrixForm[mat3]"mat3"FullSimplify[mat3-lor]g0=Join[Join[z2,-iun2,2],Join[-iun2,z2,2]];MatrixForm[g0]g1=Join[Join[z2,s1,2],Join[-s1,z2,2]];MatrixForm[g1]g2=Join[Join[z2,s2,2],Join[-s2,z2,2]];MatrixForm[g2]g3=Join[Join[z2,s3,2],Join[-s3,z2,2]];MatrixForm[g3]g5=Join[Join[iun2,z2,2],Join[z2,-iun2,2]];MatrixForm[g5]"g0-1-2-3-5"

Out[]//MatrixForm=
a11 | a12 |
a21 | a22 |
Out[]=
a
Out[]//MatrixForm=
Conjugate[a11] | Conjugate[a21] |
Conjugate[a12] | Conjugate[a22] |
Out[]=
ah
Out[]//MatrixForm=
0 | 0 |
0 | 0 |
Out[]=
z2
Out[]//MatrixForm=
0 | 1 |
1 | 0 |
Out[]//MatrixForm=
0 | - |
| 0 |
Out[]//MatrixForm=
1 | 0 |
0 | -1 |
Out[]=
s1-3
Out[]//MatrixForm=
1 | 0 |
0 | 1 |
Out[]=
iun2
Out[]//MatrixForm=
1 2 2 Abs[a11] 2 Abs[a12] 2 Abs[a21] 2 Abs[a22] | 1 2 | 1 2 | 1 2 2 Abs[a11] 2 Abs[a21] |
1 2 | 1 2 | 1 2 | 1 2 |
1 2 | 1 2 | 1 2 | 1 2 |
1 2 2 Abs[a11] 2 Abs[a12] | 1 2 | 1 2 | 1 2 2 Abs[a11] 2 Abs[a22] |
Out[]=
lor
Out[]//MatrixForm=
a11 | a12 | a21 | a22 |
a21 | a22 | a11 | a12 |
-a21 | -a22 | a11 | a12 |
a11 | a12 | -a21 | -a22 |
Out[]=
mat1
Out[]//MatrixForm=
Conjugate[a11] | Conjugate[a12] | -Conjugate[a12] | Conjugate[a11] |
Conjugate[a12] | Conjugate[a11] | Conjugate[a11] | -Conjugate[a12] |
Conjugate[a21] | Conjugate[a22] | -Conjugate[a22] | Conjugate[a21] |
Conjugate[a22] | Conjugate[a21] | Conjugate[a21] | -Conjugate[a22] |
Out[]=
mat2
Out[]//MatrixForm=
1 2 | 1 2 | 1 2 | 1 2 |
1 2 | 1 2 | 1 2 | 1 2 |
1 2 | 1 2 | 1 2 | 1 2 |
1 2 | 1 2 | 1 2 | 1 2 |
Out[]=
mat3
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]//MatrixForm=
0 | 0 | -1 | 0 |
0 | 0 | 0 | -1 |
-1 | 0 | 0 | 0 |
0 | -1 | 0 | 0 |
Out[]//MatrixForm=
0 | 0 | 0 | 1 |
0 | 0 | 1 | 0 |
0 | -1 | 0 | 0 |
-1 | 0 | 0 | 0 |
Out[]//MatrixForm=
0 | 0 | 0 | - |
0 | 0 | | 0 |
0 | | 0 | 0 |
- | 0 | 0 | 0 |
Out[]//MatrixForm=
0 | 0 | 1 | 0 |
0 | 0 | 0 | -1 |
-1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 |
Out[]//MatrixForm=
1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 |
0 | 0 | -1 | 0 |
0 | 0 | 0 | -1 |
Out[]=
g0-1-2-3-5
Out[]=

In[]:=
Out[]//MatrixForm=
0 | -1 | 0 | 0 |
1 | 0 | 0 | 0 |
0 | 0 | 0 | 1 |
0 | 0 | -1 | 0 |
Out[]=
ch
Out[]//MatrixForm=
0 | | 0 | 0 |
| 0 | 0 | 0 |
0 | 0 | 0 | - |
0 | 0 | - | 0 |
Out[]=
sig01
Out[]//MatrixForm=
0 | 1 | 0 | 0 |
-1 | 0 | 0 | 0 |
0 | 0 | 0 | -1 |
0 | 0 | 1 | 0 |
Out[]=
sig02
Out[]//MatrixForm=
| 0 | 0 | 0 |
0 | - | 0 | 0 |
0 | 0 | - | 0 |
0 | 0 | 0 | |
Out[]=
sig03
Out[]//MatrixForm=
1 | 0 | 0 | 0 |
0 | -1 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 0 | 0 | -1 |
Out[]=
sig12
Out[]//MatrixForm=
0 | | 0 | 0 |
- | 0 | 0 | 0 |
0 | 0 | 0 | |
0 | 0 | - | 0 |
Out[]=
sig13
Out[]//MatrixForm=
0 | 1 | 0 | 0 |
1 | 0 | 0 | 0 |
0 | 0 | 0 | 1 |
0 | 0 | 1 | 0 |
Out[]=
sig23
Out[]//MatrixForm=
chi1 |
chi2 |
chi3 |
chi4 |
Out[]=
chi
Out[]//MatrixForm=
zet1 |
zet2 |
zet3 |
zet4 |
Out[]=
zet
Out[]//MatrixForm=
0 | -1 | 0 | 0 |
1 | 0 | 0 | 0 |
0 | 0 | 0 | 1 |
0 | 0 | -1 | 0 |
Out[]=
ch
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]//MatrixForm=
(
)
chi1 | chi2 | chi3 | chi4 |
Out[]=
chit
Out[]//MatrixForm=
(
)
chi2 | -chi1 | -chi4 | chi3 |
Out[]=
chitch
Out[]//MatrixForm=
(
)
chi1 | chi2 | chi3 | chi4 |
Out[]=
chit
Out[]//MatrixForm=
(
)
Conjugate[chi1] | Conjugate[chi2] | Conjugate[chi3] | Conjugate[chi4] |
Out[]=
chih
Out[]//MatrixForm=
(
)
-Conjugate[chi3] | -Conjugate[chi4] | -Conjugate[chi1] | -Conjugate[chi2] |
Out[]=
chidj
Out[]//MatrixForm=
(
)
zet1 | zet2 | zet3 | zet4 |
Out[]=
zett
Out[]//MatrixForm=
(
)
Conjugate[zet1] | Conjugate[zet2] | Conjugate[zet3] | Conjugate[zet4] |
Out[]=
zeth
Out[]//MatrixForm=
(
)
-Conjugate[zet3] | -Conjugate[zet4] | -Conjugate[zet1] | -Conjugate[zet2] |
Out[]=
zetdj
Out[]//MatrixForm=
Conjugate[zet4] |
-Conjugate[zet3] |
-Conjugate[zet2] |
Conjugate[zet1] |
Out[]=
zetch
Out[]//MatrixForm=
0 | (Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]+Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) | Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]+Conjugate[chi3]Conjugate[zet3]+Conjugate[chi4]Conjugate[zet4] | -(Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2]+Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4]) |
-(Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]+Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) | 0 | Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2]-Conjugate[chi4]Conjugate[zet3]-Conjugate[chi3]Conjugate[zet4] | -(Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]-Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) |
-Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]-Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4] | -Conjugate[chi2]Conjugate[zet1]-Conjugate[chi1]Conjugate[zet2]+Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4] | 0 | -Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]+Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4] |
(Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2]+Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4]) | (Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]-Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) | Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]-Conjugate[chi3]Conjugate[zet3]+Conjugate[chi4]Conjugate[zet4] | 0 |
Out[]=
spfi
Out[]//MatrixForm=
0 | (Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]) | Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2] | -(Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2]) |
-(Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]) | 0 | Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2] | -(Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]) |
-Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2] | -Conjugate[chi2]Conjugate[zet1]-Conjugate[chi1]Conjugate[zet2] | 0 | -Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2] |
(Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2]) | (Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]) | Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2] | 0 |
Out[]=
spfitop
Out[]//MatrixForm=
0 | (Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) | Conjugate[chi3]Conjugate[zet3]+Conjugate[chi4]Conjugate[zet4] | -(Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4]) |
-(Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) | 0 | -Conjugate[chi4]Conjugate[zet3]-Conjugate[chi3]Conjugate[zet4] | -(-Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) |
-Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4] | Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4] | 0 | Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4] |
(Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4]) | (-Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) | -Conjugate[chi3]Conjugate[zet3]+Conjugate[chi4]Conjugate[zet4] | 0 |
Out[]=
spfibot
Out[]//MatrixForm=
a11 | a12 |
a21 | a22 |
Out[]=
a
Out[]=
{{Conjugate[a22]/(-Conjugate[a12]Conjugate[a21]+Conjugate[a11]Conjugate[a22]),Conjugate[a21]/(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])},{Conjugate[a12]/(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22]),Conjugate[a11]/(-Conjugate[a12]Conjugate[a21]+Conjugate[a11]Conjugate[a22])}}
Out[]=
adinv
Out[]=
{{1,0},{0,1}}
Out[]=
Transpose[Conjugate[a]].adinv/.a22(1+a12 a21)/a1
Out[]//MatrixForm=
1 | 0 | 0 | 0 |
0 | -1 | 0 | 0 |
0 | 0 | -1 | 0 |
0 | 0 | 0 | -1 |
Out[]=
gg
Out[]//MatrixForm=
(a12a21-a11a22)(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22]) | 0 | 0 | 0 |
0 | -(a12a21-a11a22)(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22]) | 0 | 0 |
0 | 0 | -(a12a21-a11a22)(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22]) | 0 |
0 | 0 | 0 | -(a12a21-a11a22)(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22]) |
Out[]=
mat4
Out[]//MatrixForm=
1 | 0 | 0 | 0 |
0 | -1 | 0 | 0 |
0 | 0 | -1 | 0 |
0 | 0 | 0 | -1 |
Out[]//MatrixForm=
0 | (Conjugate[a11chi1+a12chi2]Conjugate[a11zet1+a12zet2]-Conjugate[a21chi1+a22chi2]Conjugate[a21zet1+a22zet2]) | Conjugate[a11chi1+a12chi2]Conjugate[a11zet1+a12zet2]+Conjugate[a21chi1+a22chi2]Conjugate[a21zet1+a22zet2] | -(Conjugate[a21chi1+a22chi2]Conjugate[a11zet1+a12zet2]+Conjugate[a11chi1+a12chi2]Conjugate[a21zet1+a22zet2]) |
-(Conjugate[a11chi1+a12chi2]Conjugate[a11zet1+a12zet2]-Conjugate[a21chi1+a22chi2]Conjugate[a21zet1+a22zet2]) | 0 | Conjugate[a21chi1+a22chi2]Conjugate[a11zet1+a12zet2]+Conjugate[a11chi1+a12chi2]Conjugate[a21zet1+a22zet2] | -(Conjugate[a11chi1+a12chi2]Conjugate[a11zet1+a12zet2]+Conjugate[a21chi1+a22chi2]Conjugate[a21zet1+a22zet2]) |
-Conjugate[a11chi1+a12chi2]Conjugate[a11zet1+a12zet2]-Conjugate[a21chi1+a22chi2]Conjugate[a21zet1+a22zet2] | -Conjugate[a21chi1+a22chi2]Conjugate[a11zet1+a12zet2]-Conjugate[a11chi1+a12chi2]Conjugate[a21zet1+a22zet2] | 0 | -Conjugate[a11chi1+a12chi2]Conjugate[a11zet1+a12zet2]+Conjugate[a21chi1+a22chi2]Conjugate[a21zet1+a22zet2] |
(Conjugate[a21chi1+a22chi2]Conjugate[a11zet1+a12zet2]+Conjugate[a11chi1+a12chi2]Conjugate[a21zet1+a22zet2]) | (Conjugate[a11chi1+a12chi2]Conjugate[a11zet1+a12zet2]+Conjugate[a21chi1+a22chi2]Conjugate[a21zet1+a22zet2]) | Conjugate[a11chi1+a12chi2]Conjugate[a11zet1+a12zet2]-Conjugate[a21chi1+a22chi2]Conjugate[a21zet1+a22zet2] | 0 |
Out[]=
spfi5top
Out[]//MatrixForm=
Out[]=
spfi6top
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
spfi5top-spfi6top
Out[]//MatrixForm=
0 | ( 2 a11 2 a21 | -( 2 a11 2 a12 2 a22 | -(a11(2a21chi1zet1+a22chi2zet1+a22chi1zet2)+a12(a21chi2zet1+a21chi1zet2+2a22chi2zet2))(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22]) |
-( 2 a11 2 a21 | 0 | -(a11(2a21chi1zet1+a22chi2zet1+a22chi1zet2)+a12(a21chi2zet1+a21chi1zet2+2a22chi2zet2))(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22]) | -( 2 a11 2 a12 2 a22 |
( 2 a11 2 a12 2 a22 | (a11(2a21chi1zet1+a22chi2zet1+a22chi1zet2)+a12(a21chi2zet1+a21chi1zet2+2a22chi2zet2))(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22]) | 0 | ( 2 a11 2 a21 |
(a11(2a21chi1zet1+a22chi2zet1+a22chi1zet2)+a12(a21chi2zet1+a21chi1zet2+2a22chi2zet2))(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22]) | ( 2 a11 2 a12 2 a22 | -( 2 a11 2 a21 | 0 |
Out[]=
spfi6ctop
Out[]//MatrixForm=
0 | -((a11chi1+a12chi2)(a11zet1+a12zet2)-(a21chi1+a22chi2)(a21zet1+a22zet2)) | (a11chi1+a12chi2)(a11zet1+a12zet2)+(a21chi1+a22chi2)(a21zet1+a22zet2) | ((a21chi1+a22chi2)(a11zet1+a12zet2)+(a11chi1+a12chi2)(a21zet1+a22zet2)) |
((a11chi1+a12chi2)(a11zet1+a12zet2)-(a21chi1+a22chi2)(a21zet1+a22zet2)) | 0 | (a21chi1+a22chi2)(a11zet1+a12zet2)+(a11chi1+a12chi2)(a21zet1+a22zet2) | ((a11chi1+a12chi2)(a11zet1+a12zet2)+(a21chi1+a22chi2)(a21zet1+a22zet2)) |
-(a11chi1+a12chi2)(a11zet1+a12zet2)-(a21chi1+a22chi2)(a21zet1+a22zet2) | -(a21chi1+a22chi2)(a11zet1+a12zet2)-(a11chi1+a12chi2)(a21zet1+a22zet2) | 0 | -(a11chi1+a12chi2)(a11zet1+a12zet2)+(a21chi1+a22chi2)(a21zet1+a22zet2) |
-((a21chi1+a22chi2)(a11zet1+a12zet2)+(a11chi1+a12chi2)(a21zet1+a22zet2)) | -((a11chi1+a12chi2)(a11zet1+a12zet2)+(a21chi1+a22chi2)(a21zet1+a22zet2)) | (a11chi1+a12chi2)(a11zet1+a12zet2)-(a21chi1+a22chi2)(a21zet1+a22zet2) | 0 |
Out[]=
spfi5ctop
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
spfi5ctop-spfi6ctop
Out[]//MatrixForm=
0 | -(-(chi4Conjugate[a11]-chi3Conjugate[a12])(zet4Conjugate[a11]-zet3Conjugate[a12])+(chi4Conjugate[a21]-chi3Conjugate[a22])(zet4Conjugate[a21]-zet3Conjugate[a22])) | (chi4Conjugate[a11]-chi3Conjugate[a12])(zet4Conjugate[a11]-zet3Conjugate[a12])+(chi4Conjugate[a21]-chi3Conjugate[a22])(zet4Conjugate[a21]-zet3Conjugate[a22]) | (Conjugate[a12]((chi4zet3+chi3zet4)Conjugate[a21]-2chi3zet3Conjugate[a22])+Conjugate[a11](-2chi4zet4Conjugate[a21]+(chi4zet3+chi3zet4)Conjugate[a22])) |
(-(chi4Conjugate[a11]-chi3Conjugate[a12])(zet4Conjugate[a11]-zet3Conjugate[a12])+(chi4Conjugate[a21]-chi3Conjugate[a22])(zet4Conjugate[a21]-zet3Conjugate[a22])) | 0 | 2chi4zet4Conjugate[a11]Conjugate[a21]-(chi4zet3+chi3zet4)Conjugate[a12]Conjugate[a21]-(chi4zet3+chi3zet4)Conjugate[a11]Conjugate[a22]+2chi3zet3Conjugate[a12]Conjugate[a22] | (-(chi4Conjugate[a11]-chi3Conjugate[a12])(zet4Conjugate[a11]-zet3Conjugate[a12])-(chi4Conjugate[a21]-chi3Conjugate[a22])(zet4Conjugate[a21]-zet3Conjugate[a22])) |
-(chi4Conjugate[a11]-chi3Conjugate[a12])(zet4Conjugate[a11]-zet3Conjugate[a12])-(chi4Conjugate[a21]-chi3Conjugate[a22])(zet4Conjugate[a21]-zet3Conjugate[a22]) | Conjugate[a12]((chi4zet3+chi3zet4)Conjugate[a21]-2chi3zet3Conjugate[a22])+Conjugate[a11](-2chi4zet4Conjugate[a21]+(chi4zet3+chi3zet4)Conjugate[a22]) | 0 | -(chi4Conjugate[a11]-chi3Conjugate[a12])(zet4Conjugate[a11]-zet3Conjugate[a12])+(chi4Conjugate[a21]-chi3Conjugate[a22])(zet4Conjugate[a21]-zet3Conjugate[a22]) |
-(Conjugate[a12]((chi4zet3+chi3zet4)Conjugate[a21]-2chi3zet3Conjugate[a22])+Conjugate[a11](-2chi4zet4Conjugate[a21]+(chi4zet3+chi3zet4)Conjugate[a22])) | ((chi4Conjugate[a11]-chi3Conjugate[a12])(zet4Conjugate[a11]-zet3Conjugate[a12])+(chi4Conjugate[a21]-chi3Conjugate[a22])(zet4Conjugate[a21]-zet3Conjugate[a22])) | (chi4Conjugate[a11]-chi3Conjugate[a12])(zet4Conjugate[a11]-zet3Conjugate[a12])-(chi4Conjugate[a21]-chi3Conjugate[a22])(zet4Conjugate[a21]-zet3Conjugate[a22]) | 0 |
Out[]=
spfi5bot
Out[]//MatrixForm=
0 | -(a12a21-a11a22)chi4zet4 2 Conjugate[a11] 2 Conjugate[a12] | -(a12a21-a11a22)chi4zet4 2 Conjugate[a11] 2 Conjugate[a12] | (a12a21-a11a22)(2chi4zet4Conjugate[a11]Conjugate[a21]-(chi4zet3+chi3zet4)Conjugate[a12]Conjugate[a21]-(chi4zet3+chi3zet4)Conjugate[a11]Conjugate[a22]+2chi3zet3Conjugate[a12]Conjugate[a22]) |
(a12a21-a11a22)chi4zet4 2 Conjugate[a11] 2 Conjugate[a12] | 0 | -(a12a21-a11a22)(2chi4zet4Conjugate[a11]Conjugate[a21]-(chi4zet3+chi3zet4)Conjugate[a12]Conjugate[a21]-(chi4zet3+chi3zet4)Conjugate[a11]Conjugate[a22]+2chi3zet3Conjugate[a12]Conjugate[a22]) | (a12a21-a11a22)chi4zet4 2 Conjugate[a11] 2 Conjugate[a12] |
(a12a21-a11a22)chi4zet4 2 Conjugate[a11] 2 Conjugate[a12] | (a12a21-a11a22)(2chi4zet4Conjugate[a11]Conjugate[a21]-(chi4zet3+chi3zet4)Conjugate[a12]Conjugate[a21]-(chi4zet3+chi3zet4)Conjugate[a11]Conjugate[a22]+2chi3zet3Conjugate[a12]Conjugate[a22]) | 0 | (a12a21-a11a22)chi4zet4 2 Conjugate[a11] 2 Conjugate[a12] |
-(a12a21-a11a22)(2chi4zet4Conjugate[a11]Conjugate[a21]-(chi4zet3+chi3zet4)Conjugate[a12]Conjugate[a21]-(chi4zet3+chi3zet4)Conjugate[a11]Conjugate[a22]+2chi3zet3Conjugate[a12]Conjugate[a22]) | -(a12a21-a11a22)chi4zet4 2 Conjugate[a11] 2 Conjugate[a12] | -(a12a21-a11a22)chi4zet4 2 Conjugate[a11] 2 Conjugate[a12] | 0 |
Out[]=
spfi6bot
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
spfi5bot-spfi6bot
Out[]//MatrixForm=
0 | (-(a12Conjugate[chi3]-a11Conjugate[chi4])(a12Conjugate[zet3]-a11Conjugate[zet4])+(a22Conjugate[chi3]-a21Conjugate[chi4])(a22Conjugate[zet3]-a21Conjugate[zet4])) | (a12Conjugate[chi3]-a11Conjugate[chi4])(a12Conjugate[zet3]-a11Conjugate[zet4])+(a22Conjugate[chi3]-a21Conjugate[chi4])(a22Conjugate[zet3]-a21Conjugate[zet4]) | -(Conjugate[chi4]((a12a21+a11a22)Conjugate[zet3]-2a11a21Conjugate[zet4])+Conjugate[chi3](-2a12a22Conjugate[zet3]+(a12a21+a11a22)Conjugate[zet4])) |
-(-(a12Conjugate[chi3]-a11Conjugate[chi4])(a12Conjugate[zet3]-a11Conjugate[zet4])+(a22Conjugate[chi3]-a21Conjugate[chi4])(a22Conjugate[zet3]-a21Conjugate[zet4])) | 0 | 2a12a22Conjugate[chi3]Conjugate[zet3]-(a12a21+a11a22)Conjugate[chi4]Conjugate[zet3]-(a12a21+a11a22)Conjugate[chi3]Conjugate[zet4]+2a11a21Conjugate[chi4]Conjugate[zet4] | ((a12Conjugate[chi3]-a11Conjugate[chi4])(a12Conjugate[zet3]-a11Conjugate[zet4])+(a22Conjugate[chi3]-a21Conjugate[chi4])(a22Conjugate[zet3]-a21Conjugate[zet4])) |
-(a12Conjugate[chi3]-a11Conjugate[chi4])(a12Conjugate[zet3]-a11Conjugate[zet4])-(a22Conjugate[chi3]-a21Conjugate[chi4])(a22Conjugate[zet3]-a21Conjugate[zet4]) | Conjugate[chi4]((a12a21+a11a22)Conjugate[zet3]-2a11a21Conjugate[zet4])+Conjugate[chi3](-2a12a22Conjugate[zet3]+(a12a21+a11a22)Conjugate[zet4]) | 0 | -(a12Conjugate[chi3]-a11Conjugate[chi4])(a12Conjugate[zet3]-a11Conjugate[zet4])+(a22Conjugate[chi3]-a21Conjugate[chi4])(a22Conjugate[zet3]-a21Conjugate[zet4]) |
(Conjugate[chi4]((a12a21+a11a22)Conjugate[zet3]-2a11a21Conjugate[zet4])+Conjugate[chi3](-2a12a22Conjugate[zet3]+(a12a21+a11a22)Conjugate[zet4])) | (-(a12Conjugate[chi3]-a11Conjugate[chi4])(a12Conjugate[zet3]-a11Conjugate[zet4])-(a22Conjugate[chi3]-a21Conjugate[chi4])(a22Conjugate[zet3]-a21Conjugate[zet4])) | (a12Conjugate[chi3]-a11Conjugate[chi4])(a12Conjugate[zet3]-a11Conjugate[zet4])-(a22Conjugate[chi3]-a21Conjugate[chi4])(a22Conjugate[zet3]-a21Conjugate[zet4]) | 0 |
Out[]=
spfi5ncbot
Out[]//MatrixForm=
0 | (Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])(Conjugate[chi4]((-a11a12+a21a22)Conjugate[zet3]+(a11-a21)(a11+a21)Conjugate[zet4])+Conjugate[chi3]((a12-a22)(a12+a22)Conjugate[zet3]+(-a11a12+a21a22)Conjugate[zet4])) | -(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])Conjugate[chi4]-(a11a12+a21a22)Conjugate[zet3]+( 2 a11 2 a21 2 a12 2 a22 | -(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])(2a12a22Conjugate[chi3]Conjugate[zet3]-(a12a21+a11a22)Conjugate[chi4]Conjugate[zet3]-(a12a21+a11a22)Conjugate[chi3]Conjugate[zet4]+2a11a21Conjugate[chi4]Conjugate[zet4]) |
-(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])(Conjugate[chi4]((-a11a12+a21a22)Conjugate[zet3]+(a11-a21)(a11+a21)Conjugate[zet4])+Conjugate[chi3]((a12-a22)(a12+a22)Conjugate[zet3]+(-a11a12+a21a22)Conjugate[zet4])) | 0 | -(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])(2a12a22Conjugate[chi3]Conjugate[zet3]-(a12a21+a11a22)Conjugate[chi4]Conjugate[zet3]-(a12a21+a11a22)Conjugate[chi3]Conjugate[zet4]+2a11a21Conjugate[chi4]Conjugate[zet4]) | -(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])Conjugate[chi4]-(a11a12+a21a22)Conjugate[zet3]+( 2 a11 2 a21 2 a12 2 a22 |
(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])Conjugate[chi4]-(a11a12+a21a22)Conjugate[zet3]+( 2 a11 2 a21 2 a12 2 a22 | (Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])(2a12a22Conjugate[chi3]Conjugate[zet3]-(a12a21+a11a22)Conjugate[chi4]Conjugate[zet3]-(a12a21+a11a22)Conjugate[chi3]Conjugate[zet4]+2a11a21Conjugate[chi4]Conjugate[zet4]) | 0 | (Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])(Conjugate[chi4]((-a11a12+a21a22)Conjugate[zet3]+(a11-a21)(a11+a21)Conjugate[zet4])+Conjugate[chi3]((a12-a22)(a12+a22)Conjugate[zet3]+(-a11a12+a21a22)Conjugate[zet4])) |
(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])(2a12a22Conjugate[chi3]Conjugate[zet3]-(a12a21+a11a22)Conjugate[chi4]Conjugate[zet3]-(a12a21+a11a22)Conjugate[chi3]Conjugate[zet4]+2a11a21Conjugate[chi4]Conjugate[zet4]) | (Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])Conjugate[chi4]-(a11a12+a21a22)Conjugate[zet3]+( 2 a11 2 a21 2 a12 2 a22 | -(Conjugate[a12]Conjugate[a21]-Conjugate[a11]Conjugate[a22])(Conjugate[chi4]((-a11a12+a21a22)Conjugate[zet3]+(a11-a21)(a11+a21)Conjugate[zet4])+Conjugate[chi3]((a12-a22)(a12+a22)Conjugate[zet3]+(-a11a12+a21a22)Conjugate[zet4])) | 0 |
Out[]=
spfi6ncbot
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
spfi5ncbot-spfi6ncbot
Out[]//MatrixForm=
0 | (Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]) | Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2] | -(Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2]) |
-(Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]) | 0 | Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2] | -(Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]) |
-Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2] | -Conjugate[chi2]Conjugate[zet1]-Conjugate[chi1]Conjugate[zet2] | 0 | -Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2] |
(Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2]) | (Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]) | Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2] | 0 |
Out[]//MatrixForm=
0 | -Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2] | (Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]) | Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2] |
Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2] | 0 | (Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2]) | Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2] |
-(Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]) | -(Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2]) | 0 | -(Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]) |
-Conjugate[chi2]Conjugate[zet1]-Conjugate[chi1]Conjugate[zet2] | -Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2] | (Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]) | 0 |
Out[]=
spfitopd
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
FullSimplify[MatrixForm[spfitop+I spfitopd]]
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
FullSimplify[MatrixForm[spfitop^*-I spfitopd^*]]
Out[]//MatrixForm=
0 | Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4] | -(Conjugate[chi3]Conjugate[zet3]+Conjugate[chi4]Conjugate[zet4]) | -Conjugate[chi4]Conjugate[zet3]-Conjugate[chi3]Conjugate[zet4] |
-Conjugate[chi3]Conjugate[zet3]+Conjugate[chi4]Conjugate[zet4] | 0 | (Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4]) | Conjugate[chi3]Conjugate[zet3]+Conjugate[chi4]Conjugate[zet4] |
(Conjugate[chi3]Conjugate[zet3]+Conjugate[chi4]Conjugate[zet4]) | -(Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4]) | 0 | -(Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) |
Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4] | -Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4] | (Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) | 0 |
Out[]=
spfibotd
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
FullSimplify[MatrixForm[spfibot-I spfibotd]]
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
FullSimplify[MatrixForm[spfibot^*+I spfibotd^*]]
Out[]=

In[]:=
psi={{psi1},{psi2},{psi3},{psi4}};MatrixForm[psi]"psi"psit=Transpose[psi];MatrixForm[psit]"psit"psich=ch.Transpose[ConjugateTranspose[psi].g0];MatrixForm[psich]"psich"psichch=ch.Transpose[ConjugateTranspose[psich].g0];MatrixForm[psichch]"psichch"psi-psichch"psi-psichch"FullSimplify[ConjugateTranspose[psich].g0-Transpose[psi].ch]"ConjugateTranspose[psich].g0-Transpose[psi].ch"spfip={{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}};MatrixForm[spfip]"spfip"psitch=psit.ch;MatrixForm[psitch]"psitch"spfip[[1,2]]=FullSimplify[Flatten[psitch.sig01.psi][[1]]];spfip[[1,3]]=FullSimplify[Flatten[psitch.sig02.psi][[1]]];spfip[[1,4]]=FullSimplify[Flatten[psitch.sig03.psi][[1]]];spfip[[2,3]]=FullSimplify[Flatten[psitch.sig12.psi][[1]]];spfip[[2,4]]=FullSimplify[Flatten[psitch.sig13.psi][[1]]];spfip[[3,4]]=FullSimplify[Flatten[psitch.sig23.psi][[1]]];spfip[[2,1]]=-spfip[[1,2]];spfip[[3,1]]=-spfip[[1,3]];spfip[[4,1]]=-spfip[[1,4]];spfip[[3,2]]=-spfip[[2,3]];spfip[[4,2]]=-spfip[[2,4]];spfip[[4,3]]=-spfip[[3,4]];MatrixForm[spfip]"spfip"spfipbot=spfip/.{psi10,psi20};MatrixForm[spfipbot]"spfipbot"spfiptop=spfip/.{psi30,psi40};MatrixForm[spfiptop]"spfiptop"MatrixForm[chi]"chi"MatrixForm[chidj]"chidj"chichcon=ch.Transpose[chidj];MatrixForm[chichcon]"chichcon"MatrixForm[psi]"psi"psidj=Conjugate[psit].g0;MatrixForm[psidj]"psidj"psichcon=ch.Transpose[psidj];MatrixForm[psichcon]"psichcon"spfitop;MatrixForm[spfitop]"spfitop"spfibot;MatrixForm[spfibot]"spfibot"spfiptop;MatrixForm[spfiptop]"spfiptop"spfipbot;MatrixForm[spfipbot]"spfipbot"spfitopmod=spfitop/.{chi1psichcon[[1,1]],chi2psichcon[[2,1]],zet1psichcon[[1,1]],zet2psichcon[[2,1]]};MatrixForm[spfitopmod]"spfitopmod"MatrixForm[FullSimplify[spfitopmod-spfipbot]]"spfitopmod-spfipbot"spfibotmod=spfibot/.{chi3psichcon[[3,1]],chi4psichcon[[4,1]],zet3psichcon[[3,1]],zet4psichcon[[4,1]]};MatrixForm[spfibotmod]"spfibotmod"MatrixForm[FullSimplify[spfibotmod-spfiptop]]"spfibotmod-spfiptop"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][spfiptop,gg,gg,spfiptop],{{1,4},{2,6},{3,7},{5,8}}]]]"Activate[TensorContract[Inactive[TensorProduct][spfiptop,gg,gg,spfiptop],{{1,4},{2,6},{3,7},{5,8}}]]"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][spfipbot,gg,gg,spfipbot],{{1,4},{2,6},{3,7},{5,8}}]]]"Activate[TensorContract[Inactive[TensorProduct][spfipbot,gg,gg,spfipbot],{{1,4},{2,6},{3,7},{5,8}}]]"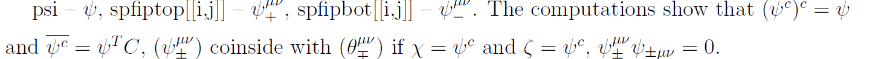
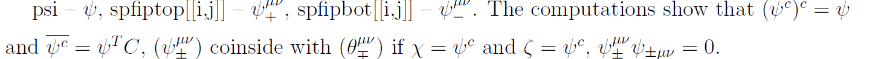
Out[]//MatrixForm=
psi1 |
psi2 |
psi3 |
psi4 |
Out[]=
psi
Out[]//MatrixForm=
(
)
psi1 | psi2 | psi3 | psi4 |
Out[]=
psit
Out[]//MatrixForm=
Conjugate[psi4] |
-Conjugate[psi3] |
-Conjugate[psi2] |
Conjugate[psi1] |
Out[]=
psich
Out[]//MatrixForm=
psi1 |
psi2 |
psi3 |
psi4 |
Out[]=
psichch
Out[]=
{{0},{0},{0},{0}}
Out[]=
psi-psichch
Out[]=
{{0,0,0,0}}
Out[]=
ConjugateTranspose[psich].g0-Transpose[psi].ch
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
spfip
Out[]//MatrixForm=
(
)
psi2 | -psi1 | -psi4 | psi3 |
Out[]=
psitch
Out[]//MatrixForm=
0 | -( 2 psi1 2 psi2 2 psi3 2 psi4 | 2 psi1 2 psi2 2 psi3 2 psi4 | 2(psi1psi2+psi3psi4) |
( 2 psi1 2 psi2 2 psi3 2 psi4 | 0 | 2psi1psi2-2psi3psi4 | ( 2 psi1 2 psi2 2 psi3 2 psi4 |
- 2 psi1 2 psi2 2 psi3 2 psi4 | -2psi1psi2+2psi3psi4 | 0 | - 2 psi1 2 psi2 2 psi3 2 psi4 |
-2(psi1psi2+psi3psi4) | -( 2 psi1 2 psi2 2 psi3 2 psi4 | 2 psi1 2 psi2 2 psi3 2 psi4 | 0 |
Out[]=
spfip
Out[]//MatrixForm=
0 | -( 2 psi3 2 psi4 | 2 psi3 2 psi4 | 2psi3psi4 |
( 2 psi3 2 psi4 | 0 | -2psi3psi4 | (- 2 psi3 2 psi4 |
- 2 psi3 2 psi4 | 2psi3psi4 | 0 | 2 psi3 2 psi4 |
-2psi3psi4 | -(- 2 psi3 2 psi4 | - 2 psi3 2 psi4 | 0 |
Out[]=
spfipbot
Out[]//MatrixForm=
0 | -( 2 psi1 2 psi2 | 2 psi1 2 psi2 | 2psi1psi2 |
( 2 psi1 2 psi2 | 0 | 2psi1psi2 | ( 2 psi1 2 psi2 |
- 2 psi1 2 psi2 | -2psi1psi2 | 0 | - 2 psi1 2 psi2 |
-2psi1psi2 | -( 2 psi1 2 psi2 | 2 psi1 2 psi2 | 0 |
Out[]=
spfiptop
Out[]//MatrixForm=
chi1 |
chi2 |
chi3 |
chi4 |
Out[]=
chi
Out[]//MatrixForm=
(
)
-Conjugate[chi3] | -Conjugate[chi4] | -Conjugate[chi1] | -Conjugate[chi2] |
Out[]=
chidj
Out[]//MatrixForm=
Conjugate[chi4] |
-Conjugate[chi3] |
-Conjugate[chi2] |
Conjugate[chi1] |
Out[]=
chichcon
Out[]//MatrixForm=
psi1 |
psi2 |
psi3 |
psi4 |
Out[]=
psi
Out[]//MatrixForm=
(
)
-Conjugate[psi3] | -Conjugate[psi4] | -Conjugate[psi1] | -Conjugate[psi2] |
Out[]=
psidj
Out[]//MatrixForm=
Conjugate[psi4] |
-Conjugate[psi3] |
-Conjugate[psi2] |
Conjugate[psi1] |
Out[]=
psichcon
Out[]//MatrixForm=
0 | (Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]) | Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2] | -(Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2]) |
-(Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2]) | 0 | Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2] | -(Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]) |
-Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2] | -Conjugate[chi2]Conjugate[zet1]-Conjugate[chi1]Conjugate[zet2] | 0 | -Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2] |
(Conjugate[chi2]Conjugate[zet1]+Conjugate[chi1]Conjugate[zet2]) | (Conjugate[chi1]Conjugate[zet1]+Conjugate[chi2]Conjugate[zet2]) | Conjugate[chi1]Conjugate[zet1]-Conjugate[chi2]Conjugate[zet2] | 0 |
Out[]=
spfitop
Out[]//MatrixForm=
0 | (Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) | Conjugate[chi3]Conjugate[zet3]+Conjugate[chi4]Conjugate[zet4] | -(Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4]) |
-(Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) | 0 | -Conjugate[chi4]Conjugate[zet3]-Conjugate[chi3]Conjugate[zet4] | -(-Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) |
-Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4] | Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4] | 0 | Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4] |
(Conjugate[chi4]Conjugate[zet3]+Conjugate[chi3]Conjugate[zet4]) | (-Conjugate[chi3]Conjugate[zet3]-Conjugate[chi4]Conjugate[zet4]) | -Conjugate[chi3]Conjugate[zet3]+Conjugate[chi4]Conjugate[zet4] | 0 |
Out[]=
spfibot
Out[]//MatrixForm=
0 | -( 2 psi1 2 psi2 | 2 psi1 2 psi2 | 2psi1psi2 |
( 2 psi1 2 psi2 | 0 | 2psi1psi2 | ( 2 psi1 2 psi2 |
- 2 psi1 2 psi2 | -2psi1psi2 | 0 | - 2 psi1 2 psi2 |
-2psi1psi2 | -( 2 psi1 2 psi2 | 2 psi1 2 psi2 | 0 |
Out[]=
spfiptop
Out[]//MatrixForm=
0 | -( 2 psi3 2 psi4 | 2 psi3 2 psi4 | 2psi3psi4 |
( 2 psi3 2 psi4 | 0 | -2psi3psi4 | (- 2 psi3 2 psi4 |
- 2 psi3 2 psi4 | 2psi3psi4 | 0 | 2 psi3 2 psi4 |
-2psi3psi4 | -(- 2 psi3 2 psi4 | - 2 psi3 2 psi4 | 0 |
Out[]=
spfipbot
Out[]//MatrixForm=
0 | (- 2 psi3 2 psi4 | 2 psi3 2 psi4 | 2psi3psi4 |
-(- 2 psi3 2 psi4 | 0 | -2psi3psi4 | -( 2 psi3 2 psi4 |
- 2 psi3 2 psi4 | 2psi3psi4 | 0 | 2 psi3 2 psi4 |
-2psi3psi4 | ( 2 psi3 2 psi4 | - 2 psi3 2 psi4 | 0 |
Out[]=
spfitopmod
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
spfitopmod-spfipbot
Out[]//MatrixForm=
0 | (- 2 psi1 2 psi2 | 2 psi1 2 psi2 | 2psi1psi2 |
-(- 2 psi1 2 psi2 | 0 | 2psi1psi2 | -(- 2 psi1 2 psi2 |
- 2 psi1 2 psi2 | -2psi1psi2 | 0 | - 2 psi1 2 psi2 |
-2psi1psi2 | (- 2 psi1 2 psi2 | 2 psi1 2 psi2 | 0 |
Out[]=
spfibotmod
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
spfibotmod-spfiptop
Out[]=
0
Out[]=
Activate[TensorContract[Inactive[TensorProduct][spfiptop,gg,gg,spfiptop],{{1,4},{2,6},{3,7},{5,8}}]]
Out[]=
0
Out[]=
Activate[TensorContract[Inactive[TensorProduct][spfipbot,gg,gg,spfipbot],{{1,4},{2,6},{3,7},{5,8}}]]
Out[]=
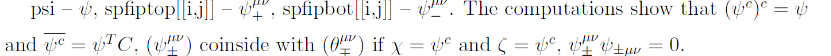
In[]:=
Out[]//MatrixForm=
ksi1 |
ksi2 |
ksi3 |
ksi4 |
Out[]=
ksi
Out[]//MatrixForm=
(
)
ksi1 | ksi2 | ksi3 | ksi4 |
Out[]=
ksit
Out[]//MatrixForm=
(
)
Conjugate[ksi1] | Conjugate[ksi2] | Conjugate[ksi3] | Conjugate[ksi4] |
Out[]=
ksih
Out[]//MatrixForm=
(
)
-Conjugate[ksi3] | -Conjugate[ksi4] | -Conjugate[ksi1] | -Conjugate[ksi2] |
Out[]=
ksidj
Out[]//MatrixForm=
Conjugate[ksi4] |
-Conjugate[ksi3] |
-Conjugate[ksi2] |
Conjugate[ksi1] |
Out[]=
ksich
Out[]//MatrixForm=
Conjugate[eta4] |
-Conjugate[eta3] |
-Conjugate[eta2] |
Conjugate[eta1] |
Out[]=
etach
Out[]=
{{-Conjugate[eta3],-Conjugate[eta4],-Conjugate[eta1],-Conjugate[eta2]}}
Out[]=
etadj
Out[]//MatrixForm=
0 |
0 |
-Conjugate[ksi2] |
Conjugate[ksi1] |
Out[]//MatrixForm=
(
)
0 | 0 | -Conjugate[ksi1] | -Conjugate[ksi2] |
Out[]//MatrixForm=
0 |
0 |
-Conjugate[eta2] |
Conjugate[eta1] |
Out[]//MatrixForm=
(
)
0 | 0 | -Conjugate[eta1] | -Conjugate[eta2] |
Out[]=
ksi ch dj eta ch dj top
Out[]=
{{Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]}}
Out[]=
ksidjtop.etachtop
Out[]//MatrixForm=
0 | 2 Conjugate[ksi1] 2 Conjugate[ksi2] | 2 Conjugate[ksi1] 2 Conjugate[ksi2] | -2Conjugate[ksi1]Conjugate[ksi2] |
- 2 Conjugate[ksi1] 2 Conjugate[ksi2] | 0 | 2Conjugate[ksi1]Conjugate[ksi2] | - 2 Conjugate[ksi1] 2 Conjugate[ksi2] |
- 2 Conjugate[ksi1] 2 Conjugate[ksi2] | -2Conjugate[ksi1]Conjugate[ksi2] | 0 | - 2 Conjugate[ksi1] 2 Conjugate[ksi2] |
2Conjugate[ksi1]Conjugate[ksi2] | 2 Conjugate[ksi1] 2 Conjugate[ksi2] | 2 Conjugate[ksi1] 2 Conjugate[ksi2] | 0 |
Out[]=
attop
Out[]=
0
Out[]=
attop^2
Out[]//MatrixForm=
0 | (Conjugate[eta1]Conjugate[ksi1]-Conjugate[eta2]Conjugate[ksi2]) | Conjugate[eta1]Conjugate[ksi1]+Conjugate[eta2]Conjugate[ksi2] | -(Conjugate[eta2]Conjugate[ksi1]+Conjugate[eta1]Conjugate[ksi2]) |
-(Conjugate[eta1]Conjugate[ksi1]-Conjugate[eta2]Conjugate[ksi2]) | 0 | Conjugate[eta2]Conjugate[ksi1]+Conjugate[eta1]Conjugate[ksi2] | -(Conjugate[eta1]Conjugate[ksi1]+Conjugate[eta2]Conjugate[ksi2]) |
-Conjugate[eta1]Conjugate[ksi1]-Conjugate[eta2]Conjugate[ksi2] | -Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2] | 0 | -Conjugate[eta1]Conjugate[ksi1]+Conjugate[eta2]Conjugate[ksi2] |
(Conjugate[eta2]Conjugate[ksi1]+Conjugate[eta1]Conjugate[ksi2]) | (Conjugate[eta1]Conjugate[ksi1]+Conjugate[eta2]Conjugate[ksi2]) | Conjugate[eta1]Conjugate[ksi1]-Conjugate[eta2]Conjugate[ksi2] | 0 |
Out[]=
bttop
Out[]=
4
2
(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2])
Out[]=
bttop^2
Out[]=
{{4}}
Out[]=
bttop^2/(ksidjtop.etachtop)^2
Out[]//MatrixForm=
0 | 2 Conjugate[eta1] 2 Conjugate[eta2] | 2 Conjugate[eta1] 2 Conjugate[eta2] | -2Conjugate[eta1]Conjugate[eta2] |
- 2 Conjugate[eta1] 2 Conjugate[eta2] | 0 | 2Conjugate[eta1]Conjugate[eta2] | - 2 Conjugate[eta1] 2 Conjugate[eta2] |
- 2 Conjugate[eta1] 2 Conjugate[eta2] | -2Conjugate[eta1]Conjugate[eta2] | 0 | - 2 Conjugate[eta1] 2 Conjugate[eta2] |
2Conjugate[eta1]Conjugate[eta2] | 2 Conjugate[eta1] 2 Conjugate[eta2] | 2 Conjugate[eta1] 2 Conjugate[eta2] | 0 |
Out[]=
cttop
Out[]=
0
Out[]=
cttop^2
Out[]=
0
Out[]=
attop bttop
Out[]=
-8
2
(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2])
Out[]=
attop cttop
Out[]=
{{-8}}
Out[]=
attop cttop/(ksidjtop.etachtop)^2
Out[]=
0
Out[]=
bttop cttop
Out[]//MatrixForm=
Conjugate[ksi4] |
-Conjugate[ksi3] |
0 |
0 |
Out[]//MatrixForm=
(
)
-Conjugate[ksi3] | -Conjugate[ksi4] | 0 | 0 |
Out[]//MatrixForm=
Conjugate[eta4] |
-Conjugate[eta3] |
0 |
0 |
Out[]//MatrixForm=
(
)
-Conjugate[eta3] | -Conjugate[eta4] | 0 | 0 |
Out[]=
ksi ch dj eta ch dj bot
Out[]=
{{-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]}}
Out[]=
ksidjbot.etachbot
Out[]//MatrixForm=
0 | 2 Conjugate[ksi3] 2 Conjugate[ksi4] | 2 Conjugate[ksi3] 2 Conjugate[ksi4] | -2Conjugate[ksi3]Conjugate[ksi4] |
- 2 Conjugate[ksi3] 2 Conjugate[ksi4] | 0 | -2Conjugate[ksi3]Conjugate[ksi4] | -- 2 Conjugate[ksi3] 2 Conjugate[ksi4] |
- 2 Conjugate[ksi3] 2 Conjugate[ksi4] | 2Conjugate[ksi3]Conjugate[ksi4] | 0 | 2 Conjugate[ksi3] 2 Conjugate[ksi4] |
2Conjugate[ksi3]Conjugate[ksi4] | - 2 Conjugate[ksi3] 2 Conjugate[ksi4] | - 2 Conjugate[ksi3] 2 Conjugate[ksi4] | 0 |
Out[]=
atbot
Out[]=
0
Out[]=
atbot^2
Out[]//MatrixForm=
0 | (Conjugate[eta3]Conjugate[ksi3]-Conjugate[eta4]Conjugate[ksi4]) | Conjugate[eta3]Conjugate[ksi3]+Conjugate[eta4]Conjugate[ksi4] | -(Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) |
-(Conjugate[eta3]Conjugate[ksi3]-Conjugate[eta4]Conjugate[ksi4]) | 0 | -Conjugate[eta4]Conjugate[ksi3]-Conjugate[eta3]Conjugate[ksi4] | -(-Conjugate[eta3]Conjugate[ksi3]-Conjugate[eta4]Conjugate[ksi4]) |
-Conjugate[eta3]Conjugate[ksi3]-Conjugate[eta4]Conjugate[ksi4] | Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4] | 0 | Conjugate[eta3]Conjugate[ksi3]-Conjugate[eta4]Conjugate[ksi4] |
(Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) | (-Conjugate[eta3]Conjugate[ksi3]-Conjugate[eta4]Conjugate[ksi4]) | -Conjugate[eta3]Conjugate[ksi3]+Conjugate[eta4]Conjugate[ksi4] | 0 |
Out[]=
btbot
Out[]=
4
2
(Conjugate[eta4]Conjugate[ksi3]-Conjugate[eta3]Conjugate[ksi4])
Out[]=
btbot^2
Out[]=
{{4}}
Out[]=
btbot^2/(ksidjbot.etachbot)^2
Out[]//MatrixForm=
0 | 2 Conjugate[eta3] 2 Conjugate[eta4] | 2 Conjugate[eta3] 2 Conjugate[eta4] | -2Conjugate[eta3]Conjugate[eta4] |
- 2 Conjugate[eta3] 2 Conjugate[eta4] | 0 | -2Conjugate[eta3]Conjugate[eta4] | -- 2 Conjugate[eta3] 2 Conjugate[eta4] |
- 2 Conjugate[eta3] 2 Conjugate[eta4] | 2Conjugate[eta3]Conjugate[eta4] | 0 | 2 Conjugate[eta3] 2 Conjugate[eta4] |
2Conjugate[eta3]Conjugate[eta4] | - 2 Conjugate[eta3] 2 Conjugate[eta4] | - 2 Conjugate[eta3] 2 Conjugate[eta4] | 0 |
Out[]=
ctbot
Out[]=
0
Out[]=
ctbot^2
Out[]=
0
Out[]=
atbot btbot
Out[]=
-8
2
(Conjugate[eta4]Conjugate[ksi3]-Conjugate[eta3]Conjugate[ksi4])
Out[]=
atbot ctbot
Out[]=
{{-8}}
Out[]=
atbot ctbot/(ksidjbot.etachbot)^2
Out[]=
0
Out[]=
btbot ctbot
Out[]=

In[]:=
Out[]=
top
Out[]//MatrixForm=
0 | u01 | u02 | u03 |
-u01 | 0 | 0 | 0 |
-u02 | 0 | 0 | 0 |
-u03 | 0 | 0 | 0 |
Out[]=
u0
Out[]//MatrixForm=
0 | u01 | u02 | u03 |
-u01 | 0 | u03 | -u02 |
-u02 | -u03 | 0 | u01 |
-u03 | u02 | -u01 | 0 |
Out[]=
u
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]=
-4(++)
2
u01
2
u02
2
u03
Out[]=
u^2
Out[]//MatrixForm=
0 | v01 | v02 | v03 |
-v01 | 0 | 0 | 0 |
-v02 | 0 | 0 | 0 |
-v03 | 0 | 0 | 0 |
Out[]=
v0
Out[]//MatrixForm=
0 | v01 | v02 | v03 |
-v01 | 0 | v03 | -v02 |
-v02 | -v03 | 0 | v01 |
-v03 | v02 | -v01 | 0 |
Out[]=
v
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]=
-4(++)
2
v01
2
v02
2
v03
Out[]=
v^2
Out[]=
-4(u01v01+u02v02+u03v03)
Out[]=
u v
Out[]//MatrixForm=
0 | Conjugate[u01] | Conjugate[u02] | Conjugate[u03] |
-Conjugate[u01] | 0 | Conjugate[u03] | -Conjugate[u02] |
-Conjugate[u02] | -Conjugate[u03] | 0 | Conjugate[u01] |
-Conjugate[u03] | Conjugate[u02] | -Conjugate[u01] | 0 |
Out[]=
umod
Out[]=
-4++
2
Conjugate[u01]
2
Conjugate[u02]
2
Conjugate[u03]
Out[]=
umod^2
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]=
-4(++)
2
Abs[u01]
2
Abs[u02]
2
Abs[u03]
Out[]=
u umod
Out[]=
-4(v01Conjugate[u01]+v02Conjugate[u02]+v03Conjugate[u03])
Out[]=
v umod
Out[]=
-
2
(v01Conjugate[u01]+v02Conjugate[u02]+v03Conjugate[u03])
2
(++)
2
Abs[u01]
2
Abs[u02]
2
Abs[u03]
Out[]=
al1
Out[]=
(2(v01Conjugate[u01]+v02Conjugate[u02]+v03Conjugate[u03]))(++)
2
Abs[u01]
2
Abs[u02]
2
Abs[u03]
Out[]=
al2
Out[]=
2
2
Abs[u01]
2
Abs[u02]
2
Abs[u03]
Out[]=
al3
Out[]//MatrixForm=
Out[]=
w
Out[]=
0
Out[]=
v w
Out[]=
-8
Out[]=
u w
Out[]=
0
Out[]=
w^2
Out[]=
bot
Out[]//MatrixForm=
0 | u01 | u02 | u03 |
-u01 | 0 | 0 | 0 |
-u02 | 0 | 0 | 0 |
-u03 | 0 | 0 | 0 |
Out[]=
u0
Out[]//MatrixForm=
0 | u01 | u02 | u03 |
-u01 | 0 | -u03 | u02 |
-u02 | u03 | 0 | -u01 |
-u03 | -u02 | u01 | 0 |
Out[]=
u
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]=
-4(++)
2
u01
2
u02
2
u03
Out[]=
u^2
Out[]//MatrixForm=
0 | v01 | v02 | v03 |
-v01 | 0 | 0 | 0 |
-v02 | 0 | 0 | 0 |
-v03 | 0 | 0 | 0 |
Out[]=
v0
Out[]//MatrixForm=
0 | v01 | v02 | v03 |
-v01 | 0 | -v03 | v02 |
-v02 | v03 | 0 | -v01 |
-v03 | -v02 | v01 | 0 |
Out[]=
v
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]=
-4(++)
2
v01
2
v02
2
v03
Out[]=
v^2
Out[]=
-4(u01v01+u02v02+u03v03)
Out[]=
u v
Out[]//MatrixForm=
0 | Conjugate[u01] | Conjugate[u02] | Conjugate[u03] |
-Conjugate[u01] | 0 | -Conjugate[u03] | Conjugate[u02] |
-Conjugate[u02] | Conjugate[u03] | 0 | -Conjugate[u01] |
-Conjugate[u03] | -Conjugate[u02] | Conjugate[u01] | 0 |
Out[]=
umod
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]=
-4(++)
2
Abs[u01]
2
Abs[u02]
2
Abs[u03]
Out[]=
u umod
Out[]=
-4(v01Conjugate[u01]+v02Conjugate[u02]+v03Conjugate[u03])
Out[]=
v umod
Out[]=
-
2
(v01Conjugate[u01]+v02Conjugate[u02]+v03Conjugate[u03])
2
(++)
2
Abs[u01]
2
Abs[u02]
2
Abs[u03]
Out[]=
al1
Out[]=
(2(v01Conjugate[u01]+v02Conjugate[u02]+v03Conjugate[u03]))(++)
2
Abs[u01]
2
Abs[u02]
2
Abs[u03]
Out[]=
al2
Out[]=
2
2
Abs[u01]
2
Abs[u02]
2
Abs[u03]
Out[]=
al3
Out[]//MatrixForm=
Out[]=
w
Out[]=

In[]:=
attopspfipbot=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][attop,gg,gg,spfipbot],{{1,3},{2,5},{4,7},{6,8}}]]]"attopspfipbot"ksidjpsitop=ksidj.psi/.{ksi30,ksi40}"ksidjpsitop"ksidjpsibot=ksidj.psi/.{ksi10,ksi20}"ksidjpsibot"atbotspfiptop=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][atbot,gg,gg,spfiptop],{{1,3},{2,5},{4,7},{6,8}}]]]"atbotspfiptop"jc0=FullSimplify[(psidj.g0.psi)[[1,1]]]"jc0"jc1=FullSimplify[(psidj.g1.psi)[[1,1]]]"jc1"jc2=FullSimplify[(psidj.g2.psi)[[1,1]]]"jc2"jc3=FullSimplify[(psidj.g3.psi)[[1,1]]]"jc3"jsqbot=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][gg,spfipbot,Conjugate[spfipbot]],{{1,3},{2,5}}]]];MatrixForm[jsqbot]"jsqbot"jsqbot2=FullSimplify[{{jc0jc0,jc0jc1,jc0jc2,jc0jc3},{jc1jc0,jc1jc1,jc1jc2,jc1jc3},{jc2jc0,jc2jc1,jc2jc2,jc2jc3},{jc3jc0,jc3jc1,jc3jc2,jc3jc3}}/.{psi10,psi20}];MatrixForm[jsqbot2]"jsqbot2"FullSimplify[jsqbot+2jsqbot2]"jsqbot+2 jsqbot2"jsqtop=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][gg,spfiptop,Conjugate[spfiptop]],{{1,3},{2,5}}]]];MatrixForm[jsqtop]"jsqtop"jsqtop2=FullSimplify[{{jc0jc0,jc0jc1,jc0jc2,jc0jc3},{jc1jc0,jc1jc1,jc1jc2,jc1jc3},{jc2jc0,jc2jc1,jc2jc2,jc2jc3},{jc3jc0,jc3jc1,jc3jc2,jc3jc3}}/.{psi30,psi40}];MatrixForm[jsqtop2]"jsqtop2"FullSimplify[jsqtop+2jsqtop2]"jsqtop+2 jsqtop2"

Out[]=
-8
2
(psi3Conjugate[ksi1]+psi4Conjugate[ksi2])
Out[]=
attopspfipbot
Out[]=
{{-psi3Conjugate[ksi1]-psi4Conjugate[ksi2]}}
Out[]=
ksidjpsitop
Out[]=
{{-psi1Conjugate[ksi3]-psi2Conjugate[ksi4]}}
Out[]=
ksidjpsibot
Out[]=
-8
2
(psi1Conjugate[ksi3]+psi2Conjugate[ksi4])
Out[]=
atbotspfiptop
Out[]=
2
Abs[psi1]
2
Abs[psi2]
2
Abs[psi3]
2
Abs[psi4]
Out[]=
jc0
Out[]=
psi2Conjugate[psi1]+psi1Conjugate[psi2]-psi4Conjugate[psi3]-psi3Conjugate[psi4]
Out[]=
jc1
Out[]=
(-psi2Conjugate[psi1]+psi1Conjugate[psi2]+psi4Conjugate[psi3]-psi3Conjugate[psi4])
Out[]=
jc2
Out[]=
2
Abs[psi1]
2
Abs[psi4]
Out[]=
jc3
Out[]//MatrixForm=
-2 2 ( 2 Abs[psi3] 2 Abs[psi4] | 2( 2 Abs[psi3] 2 Abs[psi4] | 2( 2 Abs[psi3] 2 Abs[psi4] | 2( 4 Abs[psi3] 4 Abs[psi4] |
2( 2 Abs[psi3] 2 Abs[psi4] | -2 2 (psi4Conjugate[psi3]+psi3Conjugate[psi4]) | 2 2 psi4 2 Conjugate[psi3] 2 psi3 2 Conjugate[psi4] | 2 2 Abs[psi4] |
-2( 2 Abs[psi3] 2 Abs[psi4] | 2 2 psi4 2 Conjugate[psi3] 2 psi3 2 Conjugate[psi4] | 2 2 (psi4Conjugate[psi3]-psi3Conjugate[psi4]) | 2 2 Abs[psi4] |
2( 4 Abs[psi3] 4 Abs[psi4] | 2 2 Abs[psi4] | 2 2 Abs[psi4] | -2 2 2 Abs[psi3] |
Out[]=
jsqbot
Out[]//MatrixForm=
2 ( 2 Abs[psi3] 2 Abs[psi4] | -( 2 Abs[psi3] 2 Abs[psi4] | ( 2 Abs[psi3] 2 Abs[psi4] | - 4 Abs[psi3] 4 Abs[psi4] |
-( 2 Abs[psi3] 2 Abs[psi4] | 2 (psi4Conjugate[psi3]+psi3Conjugate[psi4]) | - 2 psi4 2 Conjugate[psi3] 2 psi3 2 Conjugate[psi4] | - 2 Abs[psi4] |
( 2 Abs[psi3] 2 Abs[psi4] | - 2 psi4 2 Conjugate[psi3] 2 psi3 2 Conjugate[psi4] | - 2 (psi4Conjugate[psi3]-psi3Conjugate[psi4]) | 2 Abs[psi4] |
- 4 Abs[psi3] 4 Abs[psi4] | - 2 Abs[psi4] | 2 Abs[psi4] | 2 2 Abs[psi4] |
Out[]=
jsqbot2
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]=
jsqbot+2 jsqbot2
Out[]//MatrixForm=
-2 2 ( 2 Abs[psi1] 2 Abs[psi2] | -2( 2 Abs[psi1] 2 Abs[psi2] | 2( 2 Abs[psi1] 2 Abs[psi2] | -2 4 Abs[psi1] 4 Abs[psi2] |
-2( 2 Abs[psi1] 2 Abs[psi2] | -2 2 (psi2Conjugate[psi1]+psi1Conjugate[psi2]) | 2 2 psi2 2 Conjugate[psi1] 2 psi1 2 Conjugate[psi2] | 2 2 Abs[psi2] |
2( 2 Abs[psi1] 2 Abs[psi2] | 2 2 psi2 2 Conjugate[psi1] 2 psi1 2 Conjugate[psi2] | 2 2 (psi2Conjugate[psi1]-psi1Conjugate[psi2]) | 2 2 Abs[psi2] |
-2 4 Abs[psi1] 4 Abs[psi2] | 2 2 Abs[psi2] | 2 2 Abs[psi2] | -2 2 2 Abs[psi1] |
Out[]=
jsqtop
Out[]//MatrixForm=
2 ( 2 Abs[psi1] 2 Abs[psi2] | ( 2 Abs[psi1] 2 Abs[psi2] | ( 2 Abs[psi1] 2 Abs[psi2] | 4 Abs[psi1] 4 Abs[psi2] |
( 2 Abs[psi1] 2 Abs[psi2] | 2 (psi2Conjugate[psi1]+psi1Conjugate[psi2]) | - 2 psi2 2 Conjugate[psi1] 2 psi1 2 Conjugate[psi2] | (psi2Conjugate[psi1]+psi1Conjugate[psi2]) 2 Abs[psi1] |
( 2 Abs[psi1] 2 Abs[psi2] | - 2 psi2 2 Conjugate[psi1] 2 psi1 2 Conjugate[psi2] | - 2 (psi2Conjugate[psi1]-psi1Conjugate[psi2]) | (-psi2Conjugate[psi1]+psi1Conjugate[psi2]) 2 Abs[psi1] |
4 Abs[psi1] 4 Abs[psi2] | (psi2Conjugate[psi1]+psi1Conjugate[psi2]) 2 Abs[psi1] | (-psi2Conjugate[psi1]+psi1Conjugate[psi2]) 2 Abs[psi1] | 2 2 Abs[psi1] |
Out[]=
jsqtop2
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]=
jsqtop+2 jsqtop2
Out[]=

In[]:=
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
zer
Out[]=
{{{0,0,-1,0},{0,0,0,-1},{-1,0,0,0},{0,-1,0,0}},{{0,0,0,1},{0,0,1,0},{0,-1,0,0},{-1,0,0,0}},{{0,0,0,-},{0,0,,0},{0,,0,0},{-,0,0,0}},{{0,0,1,0},{0,0,0,-1},{-1,0,0,0},{0,1,0,0}}}
Out[]=
gmt
Out[]//MatrixForm=
0 | (bb0+bb1-bb2+bb3)(bb0-bb1+bb2+bb3) 2 Conjugate[ksi1] 2 (bb1+bb2) 2 (bb0-bb3) 2 Conjugate[ksi2] | (bb0-bb1-bb2+bb3)(bb0+bb1+bb2+bb3) 2 Conjugate[ksi1] 2 (bb1+bb2) 2 (bb0-bb3) 2 Conjugate[ksi2] | -2((bb0+bb3)Conjugate[ksi1]+(bb1+bb2)Conjugate[ksi2])((bb1-bb2)Conjugate[ksi1]+(bb0-bb3)Conjugate[ksi2]) |
-(bb0+bb1-bb2+bb3)(bb0-bb1+bb2+bb3) 2 Conjugate[ksi1] 2 (bb1+bb2) 2 (bb0-bb3) 2 Conjugate[ksi2] | 0 | -2((bb0+bb3)Conjugate[ksi1]+(bb1+bb2)Conjugate[ksi2])((bb1-bb2)Conjugate[ksi1]+(bb0-bb3)Conjugate[ksi2]) | (bb0-bb1-bb2+bb3)(bb0+bb1+bb2+bb3) 2 Conjugate[ksi1] 2 (bb1+bb2) 2 (bb0-bb3) 2 Conjugate[ksi2] |
-(bb0-bb1-bb2+bb3)(bb0+bb1+bb2+bb3) 2 Conjugate[ksi1] 2 (bb1+bb2) 2 (bb0-bb3) 2 Conjugate[ksi2] | 2((bb0+bb3)Conjugate[ksi1]+(bb1+bb2)Conjugate[ksi2])((bb1-bb2)Conjugate[ksi1]+(bb0-bb3)Conjugate[ksi2]) | 0 | (bb0+bb1-bb2+bb3)(bb0-bb1+bb2+bb3) 2 Conjugate[ksi1] 2 (bb1+bb2) 2 (bb0-bb3) 2 Conjugate[ksi2] |
2((bb0+bb3)Conjugate[ksi1]+(bb1+bb2)Conjugate[ksi2])((bb1-bb2)Conjugate[ksi1]+(bb0-bb3)Conjugate[ksi2]) | -(bb0-bb1-bb2+bb3)(bb0+bb1+bb2+bb3) 2 Conjugate[ksi1] 2 (bb1+bb2) 2 (bb0-bb3) 2 Conjugate[ksi2] | -(bb0+bb1-bb2+bb3)(bb0-bb1+bb2+bb3) 2 Conjugate[ksi1] 2 (bb1+bb2) 2 (bb0-bb3) 2 Conjugate[ksi2] | 0 |
Out[]=
ksks2top
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
ksks2top-ksks3top
Out[]//MatrixForm=
Out[]=
kset2top
Out[]//MatrixForm=
Out[]=
etks2top
Out[]//MatrixForm=
0 | 2(-bb3cc2+bb2cc3)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) | 2(bb3cc1-bb1cc3)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) | 2(-bb2cc1+bb1cc2)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) |
2(bb3cc2-bb2cc3)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) | 0 | 2(-bb3cc0+bb0cc3)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) | 2(bb2cc0-bb0cc2)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) |
2(-bb3cc1+bb1cc3)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) | 2(bb3cc0-bb0cc3)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) | 0 | 2(-bb1cc0+bb0cc1)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) |
2(bb2cc1-bb1cc2)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) | 2(-bb2cc0+bb0cc2)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) | 2(bb1cc0-bb0cc1)(Conjugate[eta2]Conjugate[ksi1]-Conjugate[eta1]Conjugate[ksi2]) | 0 |
Out[]=
bceps
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
kset2top+etks2top-bc-kset3top-bceps
Out[]//MatrixForm=
0 | (cc0+cc1-cc2+cc3)(cc0-cc1+cc2+cc3) 2 Conjugate[eta1] 2 (cc1+cc2) 2 (cc0-cc3) 2 Conjugate[eta2] | (cc0-cc1-cc2+cc3)(cc0+cc1+cc2+cc3) 2 Conjugate[eta1] 2 (cc1+cc2) 2 (cc0-cc3) 2 Conjugate[eta2] | -2((cc0+cc3)Conjugate[eta1]+(cc1+cc2)Conjugate[eta2])((cc1-cc2)Conjugate[eta1]+(cc0-cc3)Conjugate[eta2]) |
-(cc0+cc1-cc2+cc3)(cc0-cc1+cc2+cc3) 2 Conjugate[eta1] 2 (cc1+cc2) 2 (cc0-cc3) 2 Conjugate[eta2] | 0 | -2((cc0+cc3)Conjugate[eta1]+(cc1+cc2)Conjugate[eta2])((cc1-cc2)Conjugate[eta1]+(cc0-cc3)Conjugate[eta2]) | (cc0-cc1-cc2+cc3)(cc0+cc1+cc2+cc3) 2 Conjugate[eta1] 2 (cc1+cc2) 2 (cc0-cc3) 2 Conjugate[eta2] |
-(cc0-cc1-cc2+cc3)(cc0+cc1+cc2+cc3) 2 Conjugate[eta1] 2 (cc1+cc2) 2 (cc0-cc3) 2 Conjugate[eta2] | 2((cc0+cc3)Conjugate[eta1]+(cc1+cc2)Conjugate[eta2])((cc1-cc2)Conjugate[eta1]+(cc0-cc3)Conjugate[eta2]) | 0 | (cc0+cc1-cc2+cc3)(cc0-cc1+cc2+cc3) 2 Conjugate[eta1] 2 (cc1+cc2) 2 (cc0-cc3) 2 Conjugate[eta2] |
2((cc0+cc3)Conjugate[eta1]+(cc1+cc2)Conjugate[eta2])((cc1-cc2)Conjugate[eta1]+(cc0-cc3)Conjugate[eta2]) | -(cc0-cc1-cc2+cc3)(cc0+cc1+cc2+cc3) 2 Conjugate[eta1] 2 (cc1+cc2) 2 (cc0-cc3) 2 Conjugate[eta2] | -(cc0+cc1-cc2+cc3)(cc0-cc1+cc2+cc3) 2 Conjugate[eta1] 2 (cc1+cc2) 2 (cc0-cc3) 2 Conjugate[eta2] | 0 |
Out[]=
etet2top
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
etet2top-etet3top
Out[]//MatrixForm=
0 | - 2 (bb1-bb2) 2 (bb0-bb3) 2 Conjugate[ksi3] 2 Conjugate[ksi4] | 2 (bb1-bb2) 2 (bb0-bb3) 2 Conjugate[ksi3] 2 Conjugate[ksi4] | 2((bb0-bb3)Conjugate[ksi3]-(bb1+bb2)Conjugate[ksi4])((bb1+bb2)Conjugate[ksi3]-(bb0+bb3)Conjugate[ksi4]) |
-- 2 (bb1-bb2) 2 (bb0-bb3) 2 Conjugate[ksi3] 2 Conjugate[ksi4] | 0 | 2((bb0-bb3)Conjugate[ksi3]-(bb1+bb2)Conjugate[ksi4])(-(bb1-bb2)Conjugate[ksi3]+(bb0+bb3)Conjugate[ksi4]) | - 2 (bb1-bb2) 2 (bb0-bb3) 2 Conjugate[ksi3] 2 Conjugate[ksi4] |
- 2 (bb1-bb2) 2 (bb0-bb3) 2 Conjugate[ksi3] 2 Conjugate[ksi4] | -2((bb0-bb3)Conjugate[ksi3]-(bb1+bb2)Conjugate[ksi4])(-(bb1-bb2)Conjugate[ksi3]+(bb0+bb3)Conjugate[ksi4]) | 0 | -- 2 (bb1-bb2) 2 (bb0-bb3) 2 Conjugate[ksi3] 2 Conjugate[ksi4] |
2((bb0-bb3)Conjugate[ksi3]-(bb1+bb2)Conjugate[ksi4])(-(bb1-bb2)Conjugate[ksi3]+(bb0+bb3)Conjugate[ksi4]) | 2 (bb1-bb2) 2 (bb0-bb3) 2 Conjugate[ksi3] 2 Conjugate[ksi4] | - 2 (bb1-bb2) 2 (bb0-bb3) 2 Conjugate[ksi3] 2 Conjugate[ksi4] | 0 |
Out[]=
ksks2bot
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
ksks2bot-ksks3bot
Out[]//MatrixForm=
Out[]=
kset2bot
Out[]//MatrixForm=
Out[]=
etks2bot
Out[]//MatrixForm=
0 | -2(-bb3cc2+bb2cc3)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) | -2(bb3cc1-bb1cc3)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) | -2(-bb2cc1+bb1cc2)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) |
-2(bb3cc2-bb2cc3)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) | 0 | -2(-bb3cc0+bb0cc3)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) | -2(bb2cc0-bb0cc2)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) |
-2(-bb3cc1+bb1cc3)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) | -2(bb3cc0-bb0cc3)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) | 0 | -2(-bb1cc0+bb0cc1)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) |
-2(bb2cc1-bb1cc2)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) | -2(-bb2cc0+bb0cc2)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) | -2(bb1cc0-bb0cc1)(-Conjugate[eta4]Conjugate[ksi3]+Conjugate[eta3]Conjugate[ksi4]) | 0 |
Out[]=
bceps
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
kset2bot+etks2bot-bc-kset3bot-bceps
Out[]//MatrixForm=
0 | - 2 (cc1-cc2) 2 (cc0-cc3) 2 Conjugate[eta3] 2 Conjugate[eta4] | 2 (cc1-cc2) 2 (cc0-cc3) 2 Conjugate[eta3] 2 Conjugate[eta4] | 2((cc0-cc3)Conjugate[eta3]-(cc1+cc2)Conjugate[eta4])((cc1+cc2)Conjugate[eta3]-(cc0+cc3)Conjugate[eta4]) |
-- 2 (cc1-cc2) 2 (cc0-cc3) 2 Conjugate[eta3] 2 Conjugate[eta4] | 0 | 2((cc0-cc3)Conjugate[eta3]-(cc1+cc2)Conjugate[eta4])(-(cc1-cc2)Conjugate[eta3]+(cc0+cc3)Conjugate[eta4]) | - 2 (cc1-cc2) 2 (cc0-cc3) 2 Conjugate[eta3] 2 Conjugate[eta4] |
- 2 (cc1-cc2) 2 (cc0-cc3) 2 Conjugate[eta3] 2 Conjugate[eta4] | -2((cc0-cc3)Conjugate[eta3]-(cc1+cc2)Conjugate[eta4])(-(cc1-cc2)Conjugate[eta3]+(cc0+cc3)Conjugate[eta4]) | 0 | -- 2 (cc1-cc2) 2 (cc0-cc3) 2 Conjugate[eta3] 2 Conjugate[eta4] |
2((cc0-cc3)Conjugate[eta3]-(cc1+cc2)Conjugate[eta4])(-(cc1-cc2)Conjugate[eta3]+(cc0+cc3)Conjugate[eta4]) | 2 (cc1-cc2) 2 (cc0-cc3) 2 Conjugate[eta3] 2 Conjugate[eta4] | - 2 (cc1-cc2) 2 (cc0-cc3) 2 Conjugate[eta3] 2 Conjugate[eta4] | 0 |
Out[]=
etet2bot
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]=
etet2bot-etet3bot
Out[]=

In[]:=
"top calc"uu={{0,uu1,uu2,uu3},{-uu1,0,Iuu3,-Iuu2},{-uu2,-Iuu3,0,Iuu1},{-uu3,Iuu2,-Iuu1,0}};MatrixForm[uu]"uu"uu25=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][uu,uu,gg,gg],{{1,6},{2,8},{3,5},{4,7}}]]];MatrixForm[uu25]"uu25"uuhodge=FullSimplify[(1/2)Activate[TensorContract[Inactive[TensorProduct][uu,LeviCivitaTensor[4],gg,gg],{{1,7},{2,9},{5,8},{6,10}}]]];MatrixForm[uuhodge]"uuhodge"FullSimplify[uu+Iuuhodge]vv={{0,vv1,vv2,vv3},{-vv1,0,Ivv3,-Ivv2},{-vv2,-Ivv3,0,Ivv1},{-vv3,Ivv2,-Ivv1,0}};uuvv25=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][uu,vv,gg,gg],{{1,6},{2,8},{3,5},{4,7}}]]];MatrixForm[uuvv25]"uuvv25"MatrixForm[gg];uuvv=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][uu,gg,vv],{{2,3},{4,5}}]]];MatrixForm[uuvv]"uuvv"uuvvc=FullSimplify[uuvv/.{vv1(-uu2vv2-uu3vv3)/uu1}];MatrixForm[uuvvc]"uuvvc"uuvvc2=FullSimplify[uuvvc/.{uu1^2+uu2^2-uu3^2,uu1^2+uu3^2-uu2^2,uu2^2+uu3^2-uu1^2}];MatrixForm[uuvvc2]"uuvvc2"uuvvc3=FullSimplify[uuvvc2uu1/(uu3vv2-uu2vv3)];MatrixForm[uuvvc3]"uuvvc3"MatrixForm[uuvvc3+Iuu]MatrixForm[uuvv+Iuu/.{uu1vv1+uu2vv2+uu3vv30,-uu1vv1-uu2vv2-uu3vv30}]"uuvv+I uu/.{uu1 vv1+uu2 vv2+uu3 vv30}"{uu1,uu2,uu3}+Cross[{uu1,uu2,uu3},{vv1,vv2,vv3}]"{uu1,uu2,uu3}+Cross[{uu1,uu2,uu3},{vv1,vv2,vv3}]""bottom calc"uu={{0,uu1,uu2,uu3},{-uu1,0,-Iuu3,Iuu2},{-uu2,Iuu3,0,-Iuu1},{-uu3,-Iuu2,Iuu1,0}};MatrixForm[uu]"uu"uu25=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][uu,uu,gg,gg],{{1,6},{2,8},{3,5},{4,7}}]]];MatrixForm[uu25]"uu25"uuhodge=FullSimplify[(1/2)Activate[TensorContract[Inactive[TensorProduct][uu,LeviCivitaTensor[4],gg,gg],{{1,7},{2,9},{5,8},{6,10}}]]];MatrixForm[uuhodge]"uuhodge"FullSimplify[uu-Iuuhodge]vv={{0,vv1,vv2,vv3},{-vv1,0,-Ivv3,Ivv2},{-vv2,Ivv3,0,-Ivv1},{-vv3,-Ivv2,Ivv1,0}};MatrixForm[vv]"vv"uuvv25=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][uu,vv,gg,gg],{{1,6},{2,8},{3,5},{4,7}}]]];MatrixForm[uuvv25]"uuvv25"MatrixForm[gg];uuvv=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][uu,gg,vv],{{2,3},{4,5}}]]];MatrixForm[uuvv]"uuvv"uuvvc=FullSimplify[uuvv/.{vv1(-uu2vv2-uu3vv3)/uu1}];MatrixForm[uuvvc]"uuvvc"uuvvc2=FullSimplify[uuvvc/.{uu1^2+uu2^2-uu3^2,uu1^2+uu3^2-uu2^2,uu2^2+uu3^2-uu1^2}];MatrixForm[uuvvc2]"uuvvc2"uuvvc3=FullSimplify[uuvvc2(-uu1)/(uu3vv2-uu2vv3)];MatrixForm[uuvvc3]"uuvvc3"MatrixForm[uuvvc3+Iuu]MatrixForm[uuvv+Iuu/.{uu1vv1+uu2vv2+uu3vv30,-uu1vv1-uu2vv2-uu3vv30}]"uuvv+I uu/.{uu1 vv1+uu2 vv2+uu3 vv30}"{uu1,uu2,uu3}-Cross[{uu1,uu2,uu3},{vv1,vv2,vv3}]"{uu1,uu2,uu3}- Cross[{uu1,uu2,uu3},{vv1,vv2,vv3}]"

Out[]=
top calc
Out[]//MatrixForm=
0 | uu1 | uu2 | uu3 |
-uu1 | 0 | uu3 | -uu2 |
-uu2 | -uu3 | 0 | uu1 |
-uu3 | uu2 | -uu1 | 0 |
Out[]=
uu
Out[]//MatrixForm=
-4(++)
2
uu1
2
uu2
2
uu3
Out[]=
uu25
Out[]//MatrixForm=
0 | uu1 | uu2 | uu3 |
-uu1 | 0 | -uu3 | uu2 |
-uu2 | uu3 | 0 | -uu1 |
-uu3 | -uu2 | uu1 | 0 |
Out[]=
uuhodge
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]//MatrixForm=
-4(uu1vv1+uu2vv2+uu3vv3)
Out[]=
uuvv25
Out[]//MatrixForm=
uu1vv1+uu2vv2+uu3vv3 | (-uu3vv2+uu2vv3) | (uu3vv1-uu1vv3) | (-uu2vv1+uu1vv2) |
(uu3vv2-uu2vv3) | -uu1vv1-uu2vv2-uu3vv3 | uu2vv1-uu1vv2 | uu3vv1-uu1vv3 |
(-uu3vv1+uu1vv3) | -uu2vv1+uu1vv2 | -uu1vv1-uu2vv2-uu3vv3 | uu3vv2-uu2vv3 |
(uu2vv1-uu1vv2) | -uu3vv1+uu1vv3 | -uu3vv2+uu2vv3 | -uu1vv1-uu2vv2-uu3vv3 |
Out[]=
uuvv
Out[]//MatrixForm=
0 | (-uu3vv2+uu2vv3) | - (uu2uu3vv2+( 2 uu1 2 uu3 uu1 | (( 2 uu1 2 uu2 uu1 |
(uu3vv2-uu2vv3) | 0 | - ( 2 uu1 2 uu2 uu1 | - uu2uu3vv2+( 2 uu1 2 uu3 uu1 |
(uu2uu3vv2+( 2 uu1 2 uu3 uu1 | ( 2 uu1 2 uu2 uu1 | 0 | uu3vv2-uu2vv3 |
- (( 2 uu1 2 uu2 uu1 | uu2uu3vv2+( 2 uu1 2 uu3 uu1 | -uu3vv2+uu2vv3 | 0 |
Out[]=
uuvvc
Out[]//MatrixForm=
0 | (-uu3vv2+uu2vv3) | uu2(-uu3vv2+uu2vv3) uu1 | uu3(-uu3vv2+uu2vv3) uu1 |
(uu3vv2-uu2vv3) | 0 | uu3(uu3vv2-uu2vv3) uu1 | uu2(-uu3vv2+uu2vv3) uu1 |
uu2(uu3vv2-uu2vv3) uu1 | uu3(-uu3vv2+uu2vv3) uu1 | 0 | uu3vv2-uu2vv3 |
uu3(uu3vv2-uu2vv3) uu1 | uu2(uu3vv2-uu2vv3) uu1 | -uu3vv2+uu2vv3 | 0 |
Out[]=
uuvvc2
Out[]//MatrixForm=
0 | -uu1 | -uu2 | -uu3 |
uu1 | 0 | uu3 | -uu2 |
uu2 | -uu3 | 0 | uu1 |
uu3 | uu2 | -uu1 | 0 |
Out[]=
uuvvc3
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]//MatrixForm=
0 | uu1+(-uu3vv2+uu2vv3) | uu2+(uu3vv1-uu1vv3) | uu3+(-uu2vv1+uu1vv2) |
-uu1+(uu3vv2-uu2vv3) | 0 | -uu3+uu2vv1-uu1vv2 | uu2+uu3vv1-uu1vv3 |
-uu2+(-uu3vv1+uu1vv3) | uu3-uu2vv1+uu1vv2 | 0 | -uu1+uu3vv2-uu2vv3 |
-uu3+(uu2vv1-uu1vv2) | -uu2-uu3vv1+uu1vv3 | uu1-uu3vv2+uu2vv3 | 0 |
Out[]=
uuvv+I uu/.{uu1 vv1+uu2 vv2+uu3 vv30}
Out[]=
{uu1-uu3vv2+uu2vv3,uu2+uu3vv1-uu1vv3,uu3-uu2vv1+uu1vv2}
Out[]=
{uu1,uu2,uu3}+Cross[{uu1,uu2,uu3},{vv1,vv2,vv3}]
Out[]=
bottom calc
Out[]//MatrixForm=
0 | uu1 | uu2 | uu3 |
-uu1 | 0 | -uu3 | uu2 |
-uu2 | uu3 | 0 | -uu1 |
-uu3 | -uu2 | uu1 | 0 |
Out[]=
uu
Out[]//MatrixForm=
-4(++)
2
uu1
2
uu2
2
uu3
Out[]=
uu25
Out[]//MatrixForm=
0 | -uu1 | -uu2 | -uu3 |
uu1 | 0 | -uu3 | uu2 |
uu2 | uu3 | 0 | -uu1 |
uu3 | -uu2 | uu1 | 0 |
Out[]=
uuhodge
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]//MatrixForm=
0 | vv1 | vv2 | vv3 |
-vv1 | 0 | -vv3 | vv2 |
-vv2 | vv3 | 0 | -vv1 |
-vv3 | -vv2 | vv1 | 0 |
Out[]=
vv
Out[]//MatrixForm=
-4(uu1vv1+uu2vv2+uu3vv3)
Out[]=
uuvv25
Out[]//MatrixForm=
uu1vv1+uu2vv2+uu3vv3 | (uu3vv2-uu2vv3) | (-uu3vv1+uu1vv3) | (uu2vv1-uu1vv2) |
(-uu3vv2+uu2vv3) | -uu1vv1-uu2vv2-uu3vv3 | uu2vv1-uu1vv2 | uu3vv1-uu1vv3 |
(uu3vv1-uu1vv3) | -uu2vv1+uu1vv2 | -uu1vv1-uu2vv2-uu3vv3 | uu3vv2-uu2vv3 |
(-uu2vv1+uu1vv2) | -uu3vv1+uu1vv3 | -uu3vv2+uu2vv3 | -uu1vv1-uu2vv2-uu3vv3 |
Out[]=
uuvv
Out[]//MatrixForm=
0 | (uu3vv2-uu2vv3) | (uu2uu3vv2+( 2 uu1 2 uu3 uu1 | - (( 2 uu1 2 uu2 uu1 |
(-uu3vv2+uu2vv3) | 0 | - ( 2 uu1 2 uu2 uu1 | - uu2uu3vv2+( 2 uu1 2 uu3 uu1 |
- (uu2uu3vv2+( 2 uu1 2 uu3 uu1 | ( 2 uu1 2 uu2 uu1 | 0 | uu3vv2-uu2vv3 |
(( 2 uu1 2 uu2 uu1 | uu2uu3vv2+( 2 uu1 2 uu3 uu1 | -uu3vv2+uu2vv3 | 0 |
Out[]=
uuvvc
Out[]//MatrixForm=
0 | (uu3vv2-uu2vv3) | uu2(uu3vv2-uu2vv3) uu1 | uu3(uu3vv2-uu2vv3) uu1 |
(-uu3vv2+uu2vv3) | 0 | uu3(uu3vv2-uu2vv3) uu1 | uu2(-uu3vv2+uu2vv3) uu1 |
uu2(-uu3vv2+uu2vv3) uu1 | uu3(-uu3vv2+uu2vv3) uu1 | 0 | uu3vv2-uu2vv3 |
uu3(-uu3vv2+uu2vv3) uu1 | uu2(uu3vv2-uu2vv3) uu1 | -uu3vv2+uu2vv3 | 0 |
Out[]=
uuvvc2
Out[]//MatrixForm=
0 | -uu1 | -uu2 | -uu3 |
uu1 | 0 | -uu3 | uu2 |
uu2 | uu3 | 0 | -uu1 |
uu3 | -uu2 | uu1 | 0 |
Out[]=
uuvvc3
Out[]//MatrixForm=
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 |
Out[]//MatrixForm=
0 | uu1+(uu3vv2-uu2vv3) | uu2+(-uu3vv1+uu1vv3) | uu3+(uu2vv1-uu1vv2) |
-uu1+(-uu3vv2+uu2vv3) | 0 | uu3+uu2vv1-uu1vv2 | -uu2+uu3vv1-uu1vv3 |
-uu2+(uu3vv1-uu1vv3) | -uu3-uu2vv1+uu1vv2 | 0 | uu1+uu3vv2-uu2vv3 |
-uu3+(-uu2vv1+uu1vv2) | uu2-uu3vv1+uu1vv3 | -uu1-uu3vv2+uu2vv3 | 0 |
Out[]=
uuvv+I uu/.{uu1 vv1+uu2 vv2+uu3 vv30}
Out[]=
{uu1+uu3vv2-uu2vv3,uu2-uu3vv1+uu1vv3,uu3+uu2vv1-uu1vv2}
Out[]=
{uu1,uu2,uu3}- Cross[{uu1,uu2,uu3},{vv1,vv2,vv3}]
Out[]=

In[]:=
"top calc"attopsp=attop/.{ksi11,ksi20};MatrixForm[attopsp]"attopsp"attopsphodge=FullSimplify[(1/2)Activate[TensorContract[Inactive[TensorProduct][attopsp,LeviCivitaTensor[4],gg,gg],{{1,7},{2,9},{5,8},{6,10}}]]];MatrixForm[attopsphodge]"attopsphodge"FullSimplify[attopsp+Iattopsphodge]bttopsp=bttop/.{ksi11,ksi20,eta10,eta21};MatrixForm[bttopsp]"bttopsp"cttopsp=cttop/.{eta10,eta21};MatrixForm[cttopsp]"cttopsp"MatrixForm[ksidj.etach/.{ksi30,ksi40,eta30,eta40,ksi11,ksi20,eta10,eta21}]"ksidj.etach/.{ksi30,ksi40,eta30,eta40,ksi11,ksi20,eta10,eta21}"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][attopsp,gg,gg,attopsp],{{1,3},{2,5},{4,7},{6,8}}]]]"attopsp^2"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][bttopsp,gg,gg,bttopsp],{{1,3},{2,5},{4,7},{6,8}}]]]"bttopsp^2"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][cttopsp,gg,gg,cttopsp],{{1,3},{2,5},{4,7},{6,8}}]]]"cttopsp^2"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][attopsp,gg,bttopsp],{{2,3},{4,5}}]]]+Iattopsp"[attopsp,gg,bttopsp],{{2,3},{4,5}}+I attopsp]"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][bttopsp,gg,gg,cttopsp],{{1,3},{2,5},{4,7},{6,8}}]]]"bttopsp cttopsp"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][attopsp,gg,gg,cttopsp],{{1,3},{2,5},{4,7},{6,8}}]]]"attopsp cttopsp""bot calc"atbotsp=atbot/.{ksi3-1,ksi40};MatrixForm[atbotsp]"atbotsp"atbotsphodge=FullSimplify[(1/2)Activate[TensorContract[Inactive[TensorProduct][atbotsp,LeviCivitaTensor[4],gg,gg],{{1,7},{2,9},{5,8},{6,10}}]]];MatrixForm[atbotsphodge]"atbotsphodge"FullSimplify[atbotsp-Iatbotsphodge]btbotsp=btbot/.{ksi3-1,ksi40,eta30,eta41};MatrixForm[btbotsp]"btbotsp"ctbotsp=ctbot/.{eta30,eta41};MatrixForm[ctbotsp]"ctbotsp"MatrixForm[ksidj.etach/.{ksi3-1,ksi40,eta30,eta41,ksi1->0,ksi2->0,eta1->0,eta2->0}]"ksidj.etach/.{ksi3-1,ksi40,eta30,eta41,ksi1->0,ksi2->0,eta1->0,eta2->0}"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][atbotsp,gg,gg,atbotsp],{{1,3},{2,5},{4,7},{6,8}}]]]"atbotsp^2"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][btbotsp,gg,gg,btbotsp],{{1,3},{2,5},{4,7},{6,8}}]]]"btbotsp^2"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][ctbotsp,gg,gg,ctbotsp],{{1,3},{2,5},{4,7},{6,8}}]]]"ctbotsp^2"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][atbotsp,gg,btbotsp],{{2,3},{4,5}}]]]+Iatbotsp"[atbotsp,gg,btbotsp],{{2,3},{4,5}}+I atbotsp]"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][btbotsp,gg,gg,ctbotsp],{{1,3},{2,5},{4,7},{6,8}}]]]"btbotsp ctbotsp"FullSimplify[Activate[TensorContract[Inactive[TensorProduct][atbotsp,gg,gg,ctbotsp],{{1,3},{2,5},{4,7},{6,8}}]]]"atbotsp ctbotsp"

Out[]=
top calc
Out[]//MatrixForm=
0 | | 1 | 0 |
- | 0 | 0 | - |
-1 | 0 | 0 | -1 |
0 | | 1 | 0 |
Out[]=
attopsp
Out[]//MatrixForm=
0 | -1 | | 0 |
1 | 0 | 0 | 1 |
- | 0 | 0 | - |
0 | -1 | | 0 |
Out[]=
attopsphodge
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]//MatrixForm=
0 | 0 | 0 | - |
0 | 0 | 1 | 0 |
0 | -1 | 0 | 0 |
| 0 | 0 | 0 |
Out[]=
bttopsp
Out[]//MatrixForm=
0 | - | 1 | 0 |
| 0 | 0 | - |
-1 | 0 | 0 | 1 |
0 | | -1 | 0 |
Out[]=
cttopsp
Out[]//MatrixForm=
(
)
1 |
Out[]=
ksidj.etach/.{ksi30,ksi40,eta30,eta40,ksi11,ksi20,eta10,eta21}
Out[]=
0
Out[]=
attopsp^2
Out[]=
4
Out[]=
bttopsp^2
Out[]=
0
Out[]=
cttopsp^2
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]=
[attopsp,gg,bttopsp],{{2,3},{4,5}}+I attopsp]
Out[]=
0
Out[]=
bttopsp cttopsp
Out[]=
-8
Out[]=
attopsp cttopsp
Out[]=
bot calc
Out[]//MatrixForm=
0 | | 1 | 0 |
- | 0 | 0 | |
-1 | 0 | 0 | 1 |
0 | - | -1 | 0 |
Out[]=
atbotsp
Out[]//MatrixForm=
0 | 1 | - | 0 |
-1 | 0 | 0 | 1 |
| 0 | 0 | - |
0 | -1 | | 0 |
Out[]=
atbotsphodge
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]//MatrixForm=
0 | 0 | 0 | |
0 | 0 | 1 | 0 |
0 | -1 | 0 | 0 |
- | 0 | 0 | 0 |
Out[]=
btbotsp
Out[]//MatrixForm=
0 | - | 1 | 0 |
| 0 | 0 | |
-1 | 0 | 0 | -1 |
0 | - | 1 | 0 |
Out[]=
ctbotsp
Out[]//MatrixForm=
(
)
1 |
Out[]=
ksidj.etach/.{ksi3-1,ksi40,eta30,eta41,ksi1->0,ksi2->0,eta1->0,eta2->0}
Out[]=
0
Out[]=
atbotsp^2
Out[]=
4
Out[]=
btbotsp^2
Out[]=
0
Out[]=
ctbotsp^2
Out[]=
{{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}}
Out[]=
[atbotsp,gg,btbotsp],{{2,3},{4,5}}+I atbotsp]
Out[]=
0
Out[]=
btbotsp ctbotsp
Out[]=
-8
Out[]=
atbotsp ctbotsp
Out[]=

In[]:=
"top calc"uu={{0,uu1,uu2,uu3},{-uu1,0,Iuu3,-Iuu2},{-uu2,-Iuu3,0,Iuu1},{-uu3,Iuu2,-Iuu1,0}};MatrixForm[uu]"uu"ff={{0,-ee1,-ee2,-ee3},{ee1,0,-hh3,hh2},{ee2,hh3,0,-hh1},{ee3,-hh2,hh1,0}};MatrixForm[ff]"ff"ffuu=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][ff,gg,gg,uu],{{1,3},{2,5},{4,7},{6,8}}]]];MatrixForm[ffuu]"ffuu""bottom calc"uu={{0,uu1,uu2,uu3},{-uu1,0,-Iuu3,Iuu2},{-uu2,Iuu3,0,-Iuu1},{-uu3,-Iuu2,Iuu1,0}};MatrixForm[uu]"uu"ff={{0,-ee1,-ee2,-ee3},{ee1,0,-hh3,hh2},{ee2,hh3,0,-hh1},{ee3,-hh2,hh1,0}};MatrixForm[ff]"ff"ffuu=FullSimplify[Activate[TensorContract[Inactive[TensorProduct][ff,gg,gg,uu],{{1,3},{2,5},{4,7},{6,8}}]]];MatrixForm[ffuu]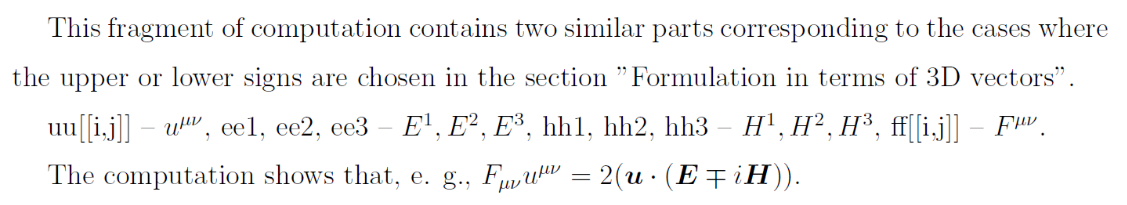
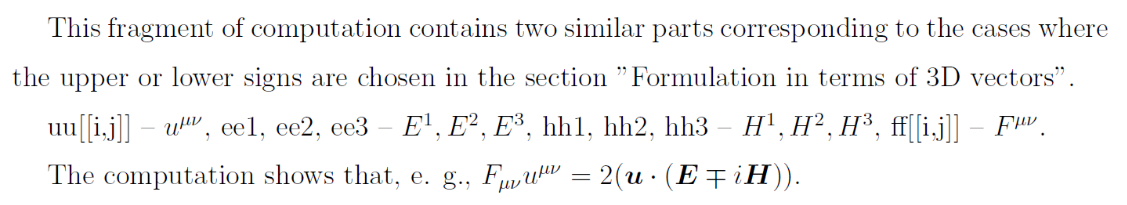
Out[]=
top calc
Out[]//MatrixForm=
0 | uu1 | uu2 | uu3 |
-uu1 | 0 | uu3 | -uu2 |
-uu2 | -uu3 | 0 | uu1 |
-uu3 | uu2 | -uu1 | 0 |
Out[]=
uu
Out[]//MatrixForm=
0 | -ee1 | -ee2 | -ee3 |
ee1 | 0 | -hh3 | hh2 |
ee2 | hh3 | 0 | -hh1 |
ee3 | -hh2 | hh1 | 0 |
Out[]=
ff
Out[]//MatrixForm=
2ee1uu1-2(hh1uu1+ee2uu2+hh2uu2+ee3uu3+hh3uu3)
Out[]=
ffuu
Out[]=
bottom calc
Out[]//MatrixForm=
0 | uu1 | uu2 | uu3 |
-uu1 | 0 | -uu3 | uu2 |
-uu2 | uu3 | 0 | -uu1 |
-uu3 | -uu2 | uu1 | 0 |
Out[]=
uu
Out[]//MatrixForm=
0 | -ee1 | -ee2 | -ee3 |
ee1 | 0 | -hh3 | hh2 |
ee2 | hh3 | 0 | -hh1 |
ee3 | -hh2 | hh1 | 0 |
Out[]=
ff
Out[]//MatrixForm=
2(ee1uu1+hh1uu1+ee2uu2+hh2uu2+ee3uu3+hh3uu3)
Out[]=

Cite this as: Andrey Akhmeteli, "The Dirac equation as a linear tensor equation for one component" from the Notebook Archive (2024), https://notebookarchive.org/2024-03-2sq7ma9
Download
