Morphological stability of electrostrictive thin films
Author
Jin Zhang
Title
Morphological stability of electrostrictive thin films
Description
Perturbed solution of the fully electromechanical coupled problem with electrostriction and lattice misfit
Category
Academic Articles & Supplements
Keywords
Morphological stability, electrostrictive films
URL
http://www.notebookarchive.org/2024-06-37t2w38/
DOI
https://notebookarchive.org/2024-06-37t2w38
Date Added
2024-06-07
Date Last Modified
2024-06-07
File Size
252.32 kilobytes
Supplements
Rights
CC BY-NC-SA 4.0

J. Zhang, P. W. Voorhees, “Morphological stability of electrostrictive thin films,” International Journal of Engineering Science, 199, (2024) 104073.
https://doi.org/10.1016/j.ijengsci.2024.104073
https://doi.org/10.1016/j.ijengsci.2024.104073
Preprint: https://arxiv.org/abs/2404.05093
Morphological stability of electrostrictive thin films
Morphological stability of electrostrictive thin films
Supplementary Material
Jin Zhang, Peter W . Voorhees
Department of Materials Science and Engineering, Northwestern University, Evanston, 60208, IL, United States
Description
Description
This notebook provides the analytical solution for the perturbed equations and an example of the dispersion curve.
General Setups
General Setups
Define symbols
Define symbols
Perturbed solution
Perturbed solution
Basic expressions
Basic expressions
Import the unknown constants determined from boundary conditions
Import the unknown constants determined from boundary conditions
Growth rate of the thin film
Growth rate of the thin film
Growth rate (Eq.38)
Growth rate (Eq.38)
In[]:=
σ=L-γ+k-λ+(2μ+3λ)-[]+-(2μ+λ)+(2μ+3λ)-(+)[]+(ϵ+(+)-(+3))[];
2
k
ε
33
*
ε
a
2
2
E
3
2
u
1
h
h
ε
33
*
ε
a
1
a
2
2
E
3
2
′
u
3
h
h
a
1
a
2
ε
33
a
1
a
2
*
ε
E
3
′
ϕ
h
h
Useful expressions
Useful expressions
Permittivity, electrostriction parameters (Eq. 16), and Lame constants for the oxide and metal substrate
In[]:=
BasicParameterRelations=ϵ,-,-(-1)(+2)+,λ,;
ϵ
r
ϵ
0
a
1
2
5
2
(-1)
ϵ
r
ϵ
0
a
2
1
3
ϵ
r
ϵ
r
2
15
2
(-1)
ϵ
r
ϵ
0
2μν
1-2ν
m
λ
2
m
μ
m
ν
1-2
m
ν
Electrostriction parameters (Eq. 27)
In[]:=
ElectrostrictionParameters=α2->1--1-3-3,β->-;
1-2ν
4μ(1-ν)
a
1
ϵ
a
2
ϵ
a
1
ϵ
a
2
ϵ
1-2ν
1-ν
ν
1-2ν
a
1
ϵ
a
2
ϵ
Planar solution of strain (Eq. 20)
In[]:=
solutionPlanarStrain33=++-ϵ;
ε
33
3λ+2μ
λ+2μ
*
ε
a
1
a
2
2(λ+2μ)
2
E
3
Equilibrium electric field (Eq. 30)
In[]:=
solutionEquilibriumElectricField=;
E
3
-(1+2β)+-4α2Δf+2μ
*
ε
2
(1+2β)
*
ε
3λ+2μ
λ+2μ
2
()
*
ε
α2ϵ
An example of the dispersion curve
An example of the dispersion curve
Materials parameters
λ, μ : Pa = kg / m s^2
ϵ : A^2 s^4 / m^3 kg
E : V / m = kg m /s^3 A
γ : J/m^2 = kg / s^2
Δf : J/m^3 = Pa = kg / m s^2
Use Unit : kg 1 nm 1 ms nA
λ, μ : Pa = kg / m s^2
ϵ : A^2 s^4 / m^3 kg
E : V / m = kg m /s^3 A
γ : J/m^2 = kg / s^2
Δf : J/m^3 = Pa = kg / m s^2
Use Unit : kg 1 nm 1 ms nA
In[]:=
scalingL=1×;scalingt=;scalingI=;(*dimesionlessscalingfactors*)MatPara=μ80.0*^9scalingL,ν0.25,0.01,50.0,80.0*^9scalingL,0.25,Δf-1.0*^8scalingL,8.854*^-12**;MatPara2=BasicParameterRelations/.MatPara;MatPara3=solutionEquilibriumElectricField/.ElectrostrictionParameters/.MatPara/.MatPara2;MatPara4=solutionPlanarStrain33/.MatPara/.MatPara2/.MatPara3;MatPara=Join[MatPara,MatPara2,MatPara3,MatPara4];Clear[MatPara2,MatPara3,MatPara4];MatParaP=2×*scalingL,γ0.1,L1*^7,0.01×*scalingL;bcConstN=bcConst/.MatPara/.MatParaP;ConstC={C1bcConstN[[1]],C2bcConstN[[2]],C30,C4bcConstN[[4]],C5bcConstN[[5]],C6bcConstN[[6]]};
9
10
3
10
9
10
2
scalingt
*
ε
ϵ
r
m
μ
2
scalingt
m
ν
2
scalingt
ϵ
0
2
scalingI
4
scalingt
3
scalingL
h
-9
10
2
scalingt
h
-9
10
Get the dimensionless growth rate
In[]:=
sigma=σ/.sol/.sold/.ConstC/.k/.MatPara/.MatParaP//Simplify;
2
h
Lγ
k
h
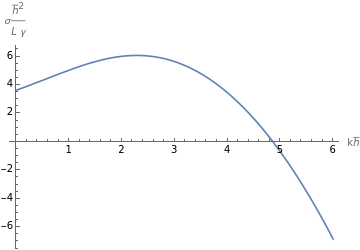
Plot the dispersion curve (Result in Fig. 5a)
In[]:=
PlotEvaluate[sigma],,0,6,AxesLabel"k","σ",ImageSizeMedium
k
h
2
h
Lγ
Out[]=
Cite this as: Jin Zhang, "Morphological stability of electrostrictive thin films" from the Notebook Archive (2024), https://notebookarchive.org/2024-06-37t2w38
Download
