Working Material

Algebraic Model of String Operations

Pavel Hajek

Author

Pavel Hajek

Title

Algebraic Model of String Operations

Description

The operations of joining and disjoining of strings have an algebraic model as a bi-Lie algebra

Algebraic Model of String Operations

Pavel Hajek

The operations of joining and disjoining of strings have an algebraic model as a bi-Lie algebra

Explanation And Example

The "interaction diagrams" below represent the operations of joining and disjoining of closed strings which are modeled as "bracelets of particles":

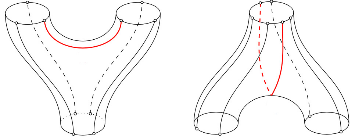
The direction of propagation is from the top to the bottom. Each red curve represents an "interaction" that amounts to a pairing that annihilates two particles and produces a scalar coefficient. There is precisely one pair of interacting particles in each diagram. The resulting strings are read off from the bottom boundary components of the depicted surfaces. If we denote the vector space generated by all strings as W, then the vector space generated by all pairs of strings is the tensor product W  W, and the diagrams correspond to a bracket μ: W  W ⟶ W and a co-bracket δ: W ⟶ W  W, respectively. In order to get independence of the choice of a particular diagram, we define the operations as sums over all permutations of input strings and all cyclic permutations of particles on each string. We can even do it in the "supersymmetric case", where each particle has an integer degree, by carefully employing a natural sign convention. In (CFL) it was shown that if the pairing is (graded) anti-symmetric and has degree d ∈ Z, then μ and δ satisfy the relations of an involutive bi-Lie algebra (IBL) of degree d. In particular, μ and δ are (graded) anti-symmetric with respect to the degree of a string computed as a sum of degrees of its particles plus d. The IBL relations can be schematically depicted as follows:

Each figure depicts a glued surface, which is interpreted as a composition of operations. The cylinder represents the identity. Algebraic relations are obtained by summing over all possible insertions of incoming strings in the top boundary components and all possible compositions of the operations that lead to the same surface.

We consider the following example of one "fermion" x and one "boson" y:

In[]:=

degrees=<|"x"->-1,"y"->0|>;pairing=<|{"x","y"}->1,{"y","x"}->-1,{"x","x"}->0,{"y","y"}->0|>;

The bracket and co-bracket of strings build from x and y can be computed in the following way:

In[]:=

{bracket["xy","yyyy"],cobracket["xyyyy"]}//Column

The anti-symmetry of δ allows us to write the result as a sum of wedge products. By sending a wedge product

⋀…⋀

to the sum

∑

δ(

)⋀

⋀…



…

⋀

, which can be seen as the sum of applications of δ to the numerators of the wedge product in all possible ways, we obtain a linear operation



on the exterior algebra ΛW of W. Likewise, using the anti-symmetry of μ, we obtain a linear operation



on ΛW by sending

⋀…⋀

∑

i,j

±μ(

)⋀

⋀…



…



… ⋀

. The notebook can evaluate arbitrary compositions of



, and ⋀:

In[]:=

bracket[wedge[cobracket["xyyyyyy"],wedge["x","y"]]]//Simplify

We can write



and



in the following succinct forms, respectively:

In[]:=

{bracket["xyyy","xyy","y"],cobracket["xyyyy","xyxyxyxx","yyyxxyyyy"]}//Column

The IBL relations can be probed as follows:

In[]:=

{jacobi["xy","xy","yyy"],cojacobi["xyxyxxxy"],drinfeld["xyxyx","yyyxxy"],involutivity["xyxxxyxxy"]}//Column

We can run automatic tests of the IBL relations on all strings of length ≤ n:

In[]:=

{testJacobi[3],testCojacobi[5],testDrinfeld[3],testInvolutivity[5]}

Here the test functions are written such that they would return wedge products of strings for which the respective relations would not hold.

Finally, let us remark that the IBL operations presented above play an important role in the formulation of string field theory (a quantum theory of strings). My plan is to extend this example to involve more aspects of string field theory, in particular the BV formalism and deformation theory.

Code

The initial data - the pairing and the degrees of particles - can be modified provided that the following requirements are satisfied:

A particle corresponds to a single letter, the pairing has a well-defined degree, and the pairing is graded anti-symmetric.

The pairing can be specified only partially as long as it is possible to deduce it for each pair of particles using the graded anti-symmetry.

In[]:=

Additional Information

Contributed By

Pavel Hajek

Keywords

◼

involutive bi-Lie algebra (IBL)

◼

graded algebra

◼

algebraic model of string operations

◼

string field theory

References

◼

The original blog post of this implementation:

◼

https://p135246.github.io/math/it/2023/04/07/canonical-IBL-algebra.html.

◼

The IBL relations were proven in the following paper:

◼

[CFL]: Cieliebak, Fukaya, Latschev: Homological algebra related to surfaces with boundary, 2015.

◼

The history of string operations and IBL relations goes back to the following seminal work:

◼

[CS]: Moira Chas, Dennis Sullivan: String Topology, 1999.

◼

My PhD thesis elaborates on this topic as well:

◼

[PH]: Pavel Hajek, IBL-Infinity Model of String Topology from Perturbative Chern-Simons Theory

Links

◼

A version of this code is also available in my Github repository.

Author Notes

◼

"Mixed inputs" like bracket[wedge[“x”,”y”],”y”] are currently not supported. Instead, wrap everything in wedge: bracket[wedge[wedge[“x”,”y”],”y"]].

Cite this as: Pavel Hajek, "Algebraic Model of String Operations" from the Notebook Archive (2024), https://notebookarchive.org/2024-07-6ij9go2