Metabolic overflow prevents ecological collapse in microbial populations
Author
Clemente Arias
Title
Metabolic overflow prevents ecological collapse in microbial populations
Description
Supplementary Material for "Metabolic overflow prevents ecological collapse in microbial populations"
Category
Academic Articles & Supplements
Keywords
URL
http://www.notebookarchive.org/2025-05-0h29lnh/
DOI
https://notebookarchive.org/2025-05-0h29lnh
Date Added
2025-05-01
Date Last Modified
2025-05-01
File Size
37.6 megabytes
Supplements
Rights
CC BY 4.0

Supplementary material to “Metabolic overflow prevents ecological collapse in microbial populations”
C . F . Arias, F . J . Acosta, F . Bertocchini, and C . Fernández - Arias (2025)
C . F . Arias, F . J . Acosta, F . Bertocchini, and C . Fernández - Arias (2025)
This notebook contains the code used to generate the figures in the main text.
This notebook contains the code used to generate the figures in the main text.
Figure 2. Delayed equations
Figure 2. Delayed equations
In[]:=
$HistoryLength=0;
In[]:=
model2=ParametricNDSolveP'[t]r1-P[t-τ]P[t],P[t/;t<0]P0,P,{t,0,40},{r,K,τ,P0};(*Model2*)
1
K
In[]:=
model3=ParametricNDSolveP'[t]r1-P[t-τ]P[t]-μP[t],P[t/;t<0]P0,P,{t,0,100},{r,K,τ,P0,μ};(*Model3*)
1
K
In[]:=
fig2=GraphicsGrid[{Map[Plot[Evaluate[P[.5,3,#,.1][t]/.model2],{t,0,40},PlotRange->All,Ticks->False]&,{2,4,8,12}],Map[Plot[Evaluate[P[.5,3,#,.1,.3][t]/.model3],{t,0,60},PlotRange->All,Ticks->False]&,{2,4,8,12}],Map[Plot[Evaluate[P[.5,3,#,.1,.4][t]/.model3],{t,0,100},PlotRange->All,Ticks->False]&,{2,4,8,12}]},ImageSize->900]
Out[]=

Figure 3. Second-order logistic model
Figure 3. Second-order logistic model
In[]:=
model4=ParametricNDSolveP''[t]r1-P[t]P[t]-μP'[t],P[0]P0,P'[0]==g0,WhenEvent[P[t]<=0,P[t]->0;P'[t]->0,"DetectionMethod"->"Interpolation"],P,{t,0,40},{r,K,P0,g0,μ},Method->{"ParametricSensitivity"->None};(*Model4*)
1
K
In[]:=
fig3B=GraphicsGrid[{Map[Plot[{3,Evaluate[P[.5,3,.1,.1,#][t]/.model4]},{t,0,40},PlotRange->All,Ticks->None]&,{0,.2,.6}]},ImageSize->900]
Out[]=

In[]:=
model1=ParametricNDSolveP'[t]r1-P[t]P[t],P[0]P0,P,{t,0,40},{r,K,P0},Method->{"ParametricSensitivity"->None};(*Model1*)
1
K
In[]:=
f3A1=Show[Map[Plot[Evaluate[P[.6#,10,.1,0,.5#][t]/.model4],{t,0,20},PlotRange->All,PlotStyle->GrayLevel[.5]]&,{.5,1,2,5,10,40}],Plot[Evaluate[P[.6/.5,10,.1][t]/.model1],{t,0,20},PlotRange->All,PlotStyle->{Orange,Thickness[.01]}],Ticks->False];
In[]:=
f3A2=Show[Map[Plot[Evaluate[P[.6#,10,.1,0.4,.5#][t]/.model4],{t,0,15},PlotRange->All,PlotStyle->GrayLevel[.5]]&,{.5,1,2,5,10,40}],Plot[Evaluate[P[.6/.5,10,.1][t]/.model1],{t,0,15},PlotRange->All,PlotStyle->{Orange,Thickness[.01]}],Ticks->False];
In[]:=
f3A3=Show[Map[Plot[Evaluate[P[.6#,10,.1,1.,.5#][t]/.model4],{t,0,15},PlotRange->All,PlotStyle->GrayLevel[.5]]&,{.5,1,2,5,10,40}],Plot[Evaluate[P[.6/.5,10,.1][t]/.model1],{t,0,15},PlotRange->All,PlotStyle->{Orange,Thickness[.01]}],Ticks->False];
In[]:=
fig3A=GraphicsGrid[{{f3A1,f3A2,f3A3}},ImageSize->1000]
Out[]=
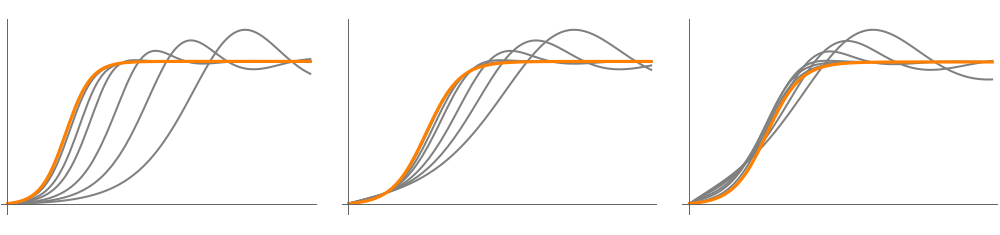
Figure 4. Second-order logistic model with resources
Figure 4. Second-order logistic model with resources
Figure 4 A
Figure 4 A
In[]:=
param4A={ρ->.2,δ->.5,τ->.5,λ->.4,α->.4,G->.5,β->.4,P0->.1,g0->0,r->10};(*Parametervalues*)
In[]:=
model6A=ParametricNDSolve[{P'[t]==g[t],g'[t]==rP[t](1-P[t]/(k1+λR[t]))-μP'[t],R'[t]==φ-δP[t]R[t],P[0]==P0,g[0]==g0,R[0]==R0,WhenEvent[P[t]<0,P[t]->0;g[t]->0]}/.param4A,{P,g,R},{t,0,1000},{R0,φ,k1,μ}];(*Model6*)
In[]:=
fig4A=Plotk1+δ+4λφ/.param4A/.{k1->5,φ->1},P[5,1,5,10][t]/.model6A,{t,0,10},Ticks->False,PlotRange->All
1
2
2
k1
δ
Out[]=

Figures 4 B-D
Figures 4 B-D
In[]:=
param4BD={ρ->.2,δ->.5,τ->.5,λ->.4,α->.4,G->.5,β->.4,P0->.1,r->.1};(*Parametervalues*)
In[]:=
model6B=ParametricNDSolve[{P'[t]==g[t],g'[t]==rP[t](1-P[t]/(k1+λR[t]))-μP'[t],R'[t]==φ-δP[t]R[t],P[0]==P0,g[0]==g0,R[0]==R0,WhenEvent[P[t]<0,P[t]->0;g[t]->0]}/.param4BD,{P,g,R},{t,0,1000},{R0,φ,k1,μ,g0}];(*Model6witharbiratyinitialvalues*)
In[]:=
fig4B=ShowMapPlotk1+δ+4λφ/.param4BD/.{k1->0,φ->9},P[#,9,0,.1,0][t]/.model6B,{t,0,33},PlotRange->{-.1,4.5},Ticks->False&,{10,400,900},PlotStyle->{Green,Orange,Red}
1
2
2
k1
δ
Out[]=

In[]:=
fig4C=ShowMapPlotk1+δ+4λφ/.param4BD/.{k1->1,φ->4},P[#,4,1,.1,0][t]/.model6B,{t,0,35},PlotRange->{-.1,5},Ticks->False&,{10,400,900},PlotStyle->{Green,Orange,Red}
1
2
2
k1
δ
Out[]=

In[]:=
model6D=ParametricNDSolveP'[t]==g[t],g'[t]==rP[t](1-P[t]/(k1+λR[t]))-μP'[t],R'[t]==φ-δP[t]R[t],P[0]==k1+δ+4λφ,g[0]==0,R[0]==+R0,WhenEvent[P[t]<0,P[t]->0;g[t]->0]/.param4BD,{P,g,R},{t,0,100},{R0,φ,k1,μ};(*Model6withinitialvaluescorrespondingtothesteadystate*)
1
2
2
k1
δ
-k1δ+δ+4λφ
δ
2
k1
2δλ
In[]:=
fig4D=ShowMapPlotk1+δ+4λφ/.param4BD/.{k1->1,φ->4},P[#,4,1,.1][t]/.model6D,{t,0,20},PlotRange->{-.1,4.5},Ticks->False&,{10,100,900},PlotStyle->{Green,Orange,Red}
1
2
2
k1
δ
Out[]=

Figures 4 E-H
Figures 4 E-H
In[]:=
param4EF={ρ->.2,δ->.5,τ->.5,λ->.4,α->.4,G->.5,β->.4,P0->.1,g0->0,r->.1};
In[]:=
Clear[model6Survival];model6Survival[R0_,φ_,k1_,μ_,g0_]:=(NDSolve[{P'[t]==g[t],g'[t]==rP[t](1-P[t]/(k1+λR[t]))-μP'[t],R'[t]==φ-δP[t]R[t],P[0]==.1,g[0]==g0,R[0]==R0,WhenEvent[P[t]<0,survival=0;"StopIntegration"],WhenEvent[Abs[P'[t]]<10^-6&&Abs[g'[t]]<10^-6,survival=1;"StopIntegration"]}/.param4EF,{P,g,R},{t,0,1000}];survival);(*Model6.Theseequationsevaluatethesurvivalofthepopulationfordifferentvaluesofinputparameters.0=extinction,1=survival*)
In[]:=
fig4E=ListDensityPlot[Flatten[Table[{φ,R0,model6Survival[R0,φ,1,.1,0]},{φ,0,20,.1},{R0,0,5000,20}],1],InterpolationOrder->0,ImageSize->250,AspectRatio->.6]
Out[]=

In[]:=
fig4F=ListDensityPlot[Flatten[Table[{φ,R0,model6Survival[R0,φ,1,.1,.5]},{φ,0,20,.1},{R0,0,5000,20}],1],InterpolationOrder->0,ImageSize->250,AspectRatio->.6]
Out[]=

In[]:=
param4GH={ρ->.2,δ->.5,τ->.5,λ->.4,α->.4,G->.5,β->.4,P0->.1,g0->0,r->.1};(*Parametervalues*)
In[]:=
Clear[model6SurvivalEq];model6SurvivalEq[R0_,φ_,k1_,μ_]:=NDSolveP'[t]==g[t],g'[t]==rP[t](1-P[t]/(k1+λR[t]))-μP'[t],R'[t]==φ-δP[t]R[t],P[0]==k1+δ+4λφ,g[0]==0,R[0]==+R0,WhenEvent[P[t]<0,survival=0;"StopIntegration"],WhenEvent[Abs[P'[t]]<10^-6&&Abs[g'[t]]<10^-6,survival=1;"StopIntegration"]/.param4GH,{P,g,R},{t,0,1000};survival;(*Model6.Theseequationsevaluatethesurvivalofthepopulationfordifferentvaluesofinputparameters.Theinitialvaluescorrespondtothesystem'ssteadystate.0=extinction,1=survival*)
1
2
2
k1
δ
-k1δ+δ+4λφ
δ
2
k1
2δλ
In[]:=
fig4G=ListDensityPlot[Flatten[Table[{φ,R0,model6SurvivalEq[R0,φ,1,.1]},{φ,0,20,.1},{R0,0,5000,20}],1],InterpolationOrder->0,ImageSize->250,AspectRatio->.6]
Out[]=

In[]:=
fig4H=ListDensityPlot[Flatten[Table[{φ,R0,model6SurvivalEq[R0,φ,2,.1]},{φ,0,20,.1},{R0,0,5000,20}],1],InterpolationOrder->0,ImageSize->250,AspectRatio->.6]
Out[]=

Figures 5.A-D. Acetate overflow
Figures 5.A-D. Acetate overflow
In[]:=
param5={δ->.5,λ->.4,G->.3,β->.1,P0->.1};(*Parametervalues*)
In[]:=
Clear[rr];rr[acetate_]:=Exp[-.01acetate](*Effectofacetateonthegrowthrate*)
In[]:=
Clear[model9];model9=ParametricNDSolve[{P'[t]==g[t],g'[t]==rrr[A[t]]P[t](1-P[t]/(k1+λR[t]))-μP'[t],R'[t]==φ-δP[t]R[t],A'[t]==α(Max[0.,g[t]-G])-βA[t]P[t],P[0]==P0,g[0]==g0,R[0]==R0,A[0]==0,WhenEvent[P[t]<0,P[t]->0;g[t]->0]}/.param5,{P,g,R,A},{t,0,1000},{R0,φ,k1,μ,g0,α,r}];(*Model9*)
In[]:=
fig5B=Plotk1+/.param5/.φ->10/.k1->1,P[600,10,1,0.3,0,0,.4][t]/.model9,P[600,10,1,.3,0,60,.4][t]/.model9,{t,0,40},AxesOrigin->{0,0},PlotRange->All
1
2
k1^2δ+4λφ
δ
Out[]=

In[]:=
Clear[model9Eq];model9Eq=ParametricNDSolveP'[t]==g[t],g'[t]==rrr[A[t]]P[t](1-P[t]/(k1+λR[t]))-μP'[t],R'[t]==φ-δP[t]R[t],A'[t]==α(Max[0.,g[t]-G])-βA[t]P[t],P[0]==k1+,g[0]==0,R[0]==+R0,A[0]==0,WhenEvent[P[t]<0,P[t]->0;g[t]->0]/.param5,{P,g,R,A},{t,0,1000},{R0,φ,k1,μ,g0,α,r};
1
2
k1^2δ+4λφ
δ
-k1δ+
δ
k1^2δ+4λφ
2δλ
In[]:=
fig5C=Plotk1+/.param5/.φ->10/.k1->1,P[300,10,1,0.3,0,0,.4][t]/.model9Eq,P[300,10,1,.3,0,100,.4][t]/.model9Eq,{t,0,40},AxesOrigin->{-1,0},PlotRange->All,PlotLegends->{"K","Without acetate","With acetate"}
1
2
k1^2δ+4λφ
δ
Out[]=
 |
|
In[]:=
fig5D=Plotk1+/.param5/.φ->.10/.k1->1,P[600,.10,1,0.3,0.5,0,.4][t]/.model9,P[600,.10,1,.2,0.5,100,.4][t]/.model9,{t,0,20},AxesOrigin->{0,0},PlotRange->All,PlotLegends->{"K","Without acetate","With acetate"}
1
2
k1^2δ+4λφ
δ
Out[]=
 |
|
Figure 5 A
Figure 5 A
In[]:=
overflow=Tabledynamics=P[10i,10,1,0.3,0,0,.4][t]/.model9Eq;i,100FindMaximum[dynamics,{t,0,.15i}][[1]]-k1+/.param5/.k1->1/.φ->10k1+/.param5/.k1->1/.φ->10,{i,.10,800,5};fig5A1=ListLinePlot[overflow,PlotRange->All];(*ThisfunctioncalculatesthevalueofoverflowusingModel9withinitialvaluescorrespondingtothesystem'ssteadystate*)
1
2
k1^2δ+4λφ
δ
1
2
k1^2δ+4λφ
δ
In[]:=
overflow=Tabledynamics=P[10i,10,1,0.3,0,100,.4][t]/.model9Eq;i,100FindMaximum[dynamics,{t,0,.15i}][[1]]-k1+/.param5/.k1->1/.φ->10k1+/.param5/.k1->1/.φ->10,{i,.1,800,5};fig5A2=ListLinePlot[overflow,PlotRange->All];
1
2
k1^2δ+4λφ
δ
1
2
k1^2δ+4λφ
δ
In[]:=
overflow=Tabledynamics=P[10i,10,1,0.3,0,200,.4][t]/.model9Eq;i,100FindMaximum[dynamics,{t,0,.15i}][[1]]-k1+/.param5/.k1->1/.φ->10k1+/.param5/.k1->1/.φ->10,{i,.1,800,5};fig5A3=ListLinePlot[overflow,PlotRange->All];
1
2
k1^2δ+4λφ
δ
1
2
k1^2δ+4λφ
δ
In[]:=
overflow=Tabledynamics=P[10i,10,1,0.3,0,400,.4][t]/.model9Eq;i,100FindMaximum[dynamics,{t,0,.15i}][[1]]-k1+/.param5/.k1->1/.φ->10k1+/.param5/.k1->1/.φ->10,{i,.1,800,5};fig5A4=ListLinePlot[overflow,PlotRange->All];
1
2
k1^2δ+4λφ
δ
1
2
k1^2δ+4λφ
δ
In[]:=
fig5A=Show[fig5A1,fig5A2,fig5A3,fig5A4,AxesOrigin->{0,0}]
Out[]=

Figures 5.E-I. Acetate overflow
Figures 5.E-I. Acetate overflow
Figures 5.E-I. Acetate overflow
Figures 5 E - G
Figures 5 E - G
In[]:=
param={δ->.5,λ->.4,G->.3,β->.1,P0->.1};(*Parametervalues*)
In[]:=
Clear[rr];rr[acetate_]:=Exp[-.01acetate](*Effectofacetateonthegrowthrate*)
In[]:=
Clear[model9Survival];model9Survival[R0_,φ_,k1_,μ_,g0_,α_,r_]:=(NDSolve[{P'[t]==g[t],g'[t]==rrr[A[t]]P[t](1-P[t]/(k1+λR[t]))-μP'[t],R'[t]==φ-δP[t]R[t],A'[t]==α(Max[0.,g[t]-G])-βA[t]P[t],P[0]==P0,g[0]==g0,R[0]==R0,A[0]==0,WhenEvent[P[t]<0,survival=0;"StopIntegration"],WhenEvent[Abs[P'[t]]<10^-6&&Abs[g'[t]]<10^-6,survival=1;"StopIntegration"]}/.param,{P,g,R,A},{t,0,1000}];survival)(*ThisfunctiondeterminesthesurvivalorextinctionofthepopulationaccordingtoModel9*)
In[]:=
fig5E=ListDensityPlot[Flatten[Table[{φ,R0,model9Survival[R0,φ,1,.2,0,0,.4]},{R0,0,5000,20},{φ,0,20,.5}],1]+Flatten[Table[{0,0,model9Survival[R0,φ,1,.2,0,100,.4]},{R0,0,5000,20},{φ,0,20,.5}],1],InterpolationOrder->0,ImageSize->250,PlotLegends->Automatic]
Out[]=
 |  |
In[]:=
fig5F=ListDensityPlot[Flatten[Table[{φ,R0,model9Survival[R0,φ,1,.2,0,0,.2]},{R0,0,5000,20},{φ,0,20,.5}],1]+Flatten[Table[{0,0,model9Survival[R0,φ,1,.2,0,100,.2]},{R0,0,5000,20},{φ,0,20,.5}],1],InterpolationOrder->0,ImageSize->250,PlotLegends->Automatic]
Out[]=
 |  |
In[]:=
fig5G=ListDensityPlot[Flatten[Table[{φ,R0,model9Survival[R0,φ,1,.2,0.5,0,.2]},{R0,0,5000,20},{φ,0,20,.5}],1]+Flatten[Table[{0,0,model9Survival[R0,φ,1,.2,0.5,100,.2]},{R0,0,5000,20},{φ,0,20,.5}],1],InterpolationOrder->0,ImageSize->250,PlotLegends->Automatic]
Out[]=
 |  |
Figures 5 H,I
Figures 5 H,I
In[]:=
param={ρ->.5,δ->.1,τ->.5,λ->4,G->1.4,β->.2};(*Parametervalues*)
In[]:=
Clear[model9SurvivalEq];model9SurvivalEq[R0_,φ_,k1_,μ_,g0_,α_,r_]:=survival=.;NDSolveP'[t]==g[t],g'[t]==rrr[M[t]]P[t](1-P[t]/(k1+λR[t]))-μP'[t],R'[t]==φ-δP[t]R[t],A'[t]==α(Max[0.,g[t]-G])-βA[t]P[t],M'[t]==.1A[t]P[t]-.1M[t],P[0]==k1+,g[0]==0,R[0]==+R0,A[0]==0,M[0]==0,WhenEvent[P[t]<0,survival=0;"StopIntegration"],WhenEvent[Abs[P'[t]]<10^-6&&Abs[g'[t]]<10^-6,survival=1;"StopIntegration"]/.param,{P,g,R,A,M},{t,0,1000};survival;(*Model9withinitialvaluescorrespondingtothesystem'ssteadystate*)
1
2
k1^2δ+4λφ
δ
-k1δ+
δ
k1^2δ+4λφ
2δλ
In[]:=
Off[NDSolve::evcvmit]
In[]:=
fig5H=ListDensityPlot[Flatten[Table[{φ,R0,model9SurvivalEq[R0,φ,1,.2,0,0,.4]},{R0,0,5000,20},{φ,0,20,.5}],1]+Flatten[Table[{0,0,model9SurvivalEq[R0,φ,1,.2,0,100,.4]},{R0,0,5000,20},{φ,0,20,.5}],1],InterpolationOrder->0,ImageSize->250,PlotLegends->Automatic]
Out[]=
 |  |
In[]:=
fig5I=ListDensityPlot[Flatten[Table[{φ,R0,model9SurvivalEq[R0,φ,1,.2,0,0,.2]},{R0,0,5000,20},{φ,0,20,.5}],1]+Flatten[Table[{0,0,model9SurvivalEq[R0,φ,1,.2,0,100,.2]},{R0,0,5000,20},{φ,0,20,.5}],1],InterpolationOrder->0,ImageSize->250,PlotLegends->Automatic]
Out[]=
 |  |
Figures 6 A-C. Two competing populations without acetate overflow
Figures 6 A-C. Two competing populations without acetate overflow
In[]:=
param6={δ1->.5,δ2->.5,G->.5,β->.4,P0->.1};(*Parametervalues*)
In[]:=
model10=ParametricNDSolve[{P1'[t]==g1[t],g1'[t]==r1P1[t](1-P1[t]/(k1+λ1R[t]))-μ1P1'[t],P2'[t]==g2[t],g2'[t]==r2P2[t](1-P2[t]/(k2+λ2R[t]))-μ2P2'[t],R'[t]==φ-δ1P1[t]R[t]-δ2P2[t]R[t],P1[0]==P0,g1[0]==0,P2[0]==P0,g2[0]==0,R[0]==R0,WhenEvent[P1[t]<0,P1[t]->0;g1[t]->0],WhenEvent[P2[t]<0,P2[t]->0;g2[t]->0]}/.param6,{P1,g1,P2,g2,R},{t,0,1000},{R0,φ,r1,μ1,λ1,r2,μ2,λ2,k1,k2}];(*Model10*)
In[]:=
fig6A=Plot[{P1[80,20,.15,.2,.3,.1,.2,.5,0,0][t]/.model10,P2[80,20,.15,.2,.3,.1,.2,.5,0,0][t]/.model10},{t,0,70},PlotRange->All,ImageSize->300,AxesOrigin->{0,0},Ticks->False]
Out[]=

In[]:=
fig6B=Plot[{P1[100,1,.15,.2,.3,.1,.2,.5,0,0][t]/.model10,P2[100,1,.15,.2,.3,.1,.2,.5,0,0][t]/.model10},{t,0,80},PlotRange->All,ImageSize->300,AxesOrigin->{0,0},Ticks->False]
Out[]=

In[]:=
fig6C=Plot[{P1[200,.5,.15,.2,.3,.1,.2,.5,0,0][t]/.model10,P2[200,.5,.15,.2,.3,.1,.2,.5,0,0][t]/.model10},{t,0,40},PlotRange->All,ImageSize->300,AxesOrigin->{0,0},Ticks->False]
Out[]=

In[]:=
fig6D=Plot[{P1[800,2,.2,.2,.6,.5,.2,.5,2,3][t]/.model10,P2[800,2,.2,.2,.6,.5,.2,.5,2,3][t]/.model10},{t,0,40},PlotRange->All,ImageSize->300,AxesOrigin->{0,0},Ticks->False]
Out[]=
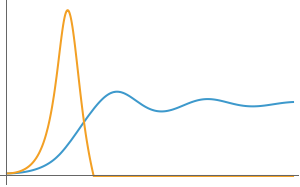
In[]:=
GraphicsGrid[{{fig6A,fig6B,fig6C,fig6D}},ImageSize->900]
Out[]=

In[]:=
model10Eq=ParametricNDSolveP1'[t]==g1[t],g1'[t]==r1P1[t](1-P1[t]/(k1+λ1R[t]))-μ1P1'[t],P2'[t]==g2[t],g2'[t]==r2P2[t](1-P2[t]/(k2+λ2R[t]))-μ2P2'[t],R'[t]==φ-δ1P1[t]R[t]-δ2P2[t]R[t],P1[0]==k1--+,g1[0]==0,P2[0]==k2--+,g2[0]==0,R[0]==+R0,WhenEvent[P1[t]<0,P1[t]->0;g1[t]->0],WhenEvent[P2[t]<0,P2[t]->0;g2[t]->0]/.param6,{P1,g1,P2,g2,R},{t,0,1000},{R0,φ,r1,μ1,λ1,r2,μ2,λ2,k1,k2};(*Model10withiniticalconditionscorrespondingtothesystem'ssteadystate*)
k1δ1λ1
2(δ1λ1+δ2λ2)
k2δ2λ1
2(δ1λ1+δ2λ2)
λ1-4(-δ1λ1-δ2λ2)φ
2
(-k1δ1-k2δ2)
2(δ1λ1+δ2λ2)
k1δ1λ2
2(δ1λ1+δ2λ2)
k2δ2λ2
2(δ1λ1+δ2λ2)
λ2-4(-δ1λ1-δ2λ2)φ
2
(-k1δ1-k2δ2)
2(δ1λ1+δ2λ2)
-k1δ1-k2δ2+-4(-δ1λ1-δ2λ2)φ
2
(-k1δ1-k2δ2)
2(δ1λ1+δ2λ2)
In[]:=
fig6E=Show[Plot[{P1[80,20,.15,.2,.3,.1,.2,.5,0,0][0]/.model10Eq,P2[80,20,.15,.2,.3,.1,.2,.5,0,0][0]/.model10Eq},{t,-5,0},PlotRange->All,ImageSize->300,AxesOrigin->{-5,0},Ticks->False],Plot[{P1[80,20,.15,.2,.3,.1,.2,.5,0,0][t]/.model10Eq,P2[80,20,.15,.2,.3,.1,.2,.5,0,0][t]/.model10Eq},{t,0,60}]]
Out[]=

In[]:=
Plot[{P1[100,1,.15,.2,.3,.1,.2,.5,0,0][t]/.model10Eq,P2[100,1,.15,.2,.3,.1,.2,.5,0,0][t]/.model10Eq},{t,0,80},PlotRange->All,ImageSize->300,AxesOrigin->{0,0},Ticks->False]
Out[]=

In[]:=
fig6F=Show[Plot[{P1[300,5,.15,.2,.3,.1,.2,.5,0,0][0]/.model10Eq,P2[300,5,.15,.2,.3,.1,.2,.5,0,0][0]/.model10Eq},{t,-5,0},PlotRange->All,ImageSize->300,AxesOrigin->{-5,0},Ticks->False],Plot[{P1[300,5,.15,.2,.3,.1,.2,.5,0,0][t]/.model10Eq,P2[300,5,.15,.2,.3,.1,.2,.5,0,0][t]/.model10Eq},{t,0,40}]]
Out[]=

In[]:=
fig6G=Show[Plot[{P1[100,1,.15,.2,.3,.1,.2,.5,0,0][0]/.model10Eq,P2[100,1,.15,.2,.3,.1,.2,.5,0,0][0]/.model10Eq},{t,-5,0},PlotRange->All,ImageSize->300,AxesOrigin->{-5,0},Ticks->False],Plot[{P1[100,1,.15,.2,.3,.1,.2,.5,0,0][t]/.model10Eq,P2[100,1,.15,.2,.3,.1,.2,.5,0,0][t]/.model10Eq},{t,0,20}]]
Out[]=
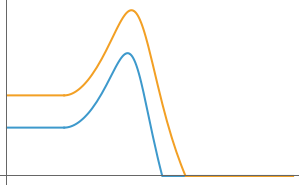
In[]:=
fig6H=Show[Plot[{P1[1000,1,.25,.2,.3,.3,.2,.5,2,1][0]/.model10Eq,P2[1000,1,.25,.2,.3,.3,.2,.5,2,1][0]/.model10Eq},{t,-5,0},PlotRange->All,ImageSize->300,AxesOrigin->{-5,0},Ticks->False],Plot[{P1[1000,1,.25,.2,.3,.3,.2,.5,2,1][t]/.model10Eq,P2[1000,1,.25,.2,.3,.3,.2,.5,2,1][t]/.model10Eq},{t,0,15}]]
Out[]=

In[]:=
GraphicsGrid[{{fig6A,fig6B,fig6C,fig6D},{fig6E,fig6F,fig6G,fig6H}},ImageSize->900]
Out[]=

Figures 6 D,H and 7. Two competing populations with acetate overflow
Figures 6 D,H and 7. Two competing populations with acetate overflow
In[]:=
Clear[rr];rr[acetate_]:=Exp[-.01acetate](*Effectofacetateonthegrowthrate*)
In[]:=
Clear[model10AO];model10AO[P0_,R0_,φ_,δ_,k1_,r1_,μ1_,λ1_,g01_,α1_,G1_,k2_,r2_,μ2_,λ2_,g02_,α2_,G2_,β_]:=(survival1=1;survival2=1;dynamics=NDSolve[{P1'[t]==a1[t]g1[t],g1'[t]==a1[t](r1rr[A[t]]P1[t](1-P1[t]/(k1+λ1R[t]))-μ1P1'[t]),P2'[t]==a2[t]g2[t],g2'[t]==a2[t](r2rr[A[t]]P2[t](1-P2[t]/(k2+λ2R[t]))-μ2P2'[t]),A'[t]==α1(Max[0.,g1[t]-G1])+α2(Max[0.,g2[t]-G2])-βA[t]P1[t]-βA[t]P2[t],R'[t]==φ-δP1[t]R[t]-δP2[t]R[t],P1[0]==P0,g1[0]==g01,P2[0]==P0,g2[0]==g02,A[0]==0,R[0]==R0,a1[0]==1,a2[0]==1,s1[0]==-1,s2[0]==-1,WhenEvent[P1[t]<0,survival1=0;s1[t]->0;a1[t]->0],WhenEvent[P2[t]<0,survival2=0;s2[t]->0;a2[t]->0]},{P1,g1,P2,g2,A,R,s1,s2,a1,a2},{t,0,500},DiscreteVariables->{a1,a2,s1,s2}];{survival1,survival2})(*Model10withacetateoverflow.ItisusedtogenerateFigures6D,HandFigure7*)
In[]:=
Clear[model10AOEq];model10AOEq[P0_,R0_,φ_,δ_,k1_,r1_,μ1_,λ1_,α1_,G1_,k2_,r2_,μ2_,λ2_,α2_,G2_,β_]:=survival1=1;survival2=1;dynamics=NDSolveP1'[t]==a1[t]g1[t],g1'[t]==a1[t](r1rr[A[t]]P1[t](1-P1[t]/(k1+λ1R[t]))-μ1P1'[t]),P2'[t]==a2[t]g2[t],g2'[t]==a2[t](r2rr[A[t]]P2[t](1-P2[t]/(k2+λ2R[t]))-μ2P2'[t]),A'[t]==α1(Max[0.,g1[t]-G1])+α2(Max[0.,g2[t]-G2])-βA[t]P1[t]-βA[t]P2[t],R'[t]==φ-δP1[t]R[t]-δP2[t]R[t],P1[0]==2k1--+δ+2k1k2δ+δ+4λ1φ+4λ2φ,g1[0]==0,P2[0]==2k2--+δ+2k1k2δ+δ+4λ1φ+4λ2φ,g2[0]==0,A[0]==0,R[0]==+R0,a1[0]==1,a2[0]==1,s1[0]==-1,s2[0]==-1,WhenEvent[P1[t]<0,survival1=0;s1[t]->0;a1[t]->0],WhenEvent[P2[t]<0,survival2=0;s2[t]->0;a2[t]->0],{P1,g1,P2,g2,A,R,s1,s2,a1,a2},{t,0,500},DiscreteVariables->{a1,a2,s1,s2};{survival1,survival2};(*Model10withacetateoverflowwithinitialconditionscorrespondingtothesteadystate.ItisusedtogenerateFigures6D,HandFigure7*)
1
2
k1δλ1
δλ1+δλ2
k2δλ1
δλ1+δλ2
δ
λ12
k1
2
k2
δλ1+δλ2
1
2
k1δλ2
δλ1+δλ2
k2δλ2
δλ1+δλ2
δ
λ22
k1
2
k2
δλ1+δλ2
-k1δ-k2δ+δ+2k1k2δ+δ+4λ1φ+4λ2φ
δ
2
k1
2
k2
2(δλ1+δλ2)
In[]:=
solution[P0_,R0_,φ_,r1_,μ1_,λ1_,r2_,μ2_,λ2_,k1_,k2_,α_,G_,β_]:=(model10AO[P0,R0,φ,.5,k1,r1,μ1,λ1,0,0,0,k2,r2,μ2,λ2,0,0,0,β];dyn1=dynamics;model10AO[P0,R0,φ,.5,k1,r1,μ1,λ1,0,α,G,k2,r2,μ2,λ2,0,α,G,β];dyn2=dynamics;model10AOEq[P0,R0,φ,.5,k1,r1,μ1,λ1,0,0,k2,r2,μ2,λ2,0,0,β];dyn1eq=dynamics;model10AOEq[P0,R0,φ,.5,k1,r1,μ1,λ1,α,G,k2,r2,μ2,λ2,α,G,β];dyn2eq=dynamics;)(*ThisfunctiongeneratesthedynamicsofModel10withandwithoutacetateoverflow,bothforarbitraryinitialconditionsandstartingfromthesteadystate.ItisusedtogenerateFigs.6Dand6H*)
In[]:=
solution[.1,80,20,.15,.2,.3,.1,.2,.5,0,0,5000,0.1,.1];
In[]:=
GraphicsGrid[{{fig6A=Plot[{P1[t]/.dyn1,P2[t]/.dyn1},{t,0,60},Ticks->False],fig6E=Show[Plot[{P1[t]/.dyn1eq,P2[t]/.dyn1eq},{t,0,40},PlotRange->All,ImageSize->300,AxesOrigin->{-5,0},Ticks->False],Plot[{P1[0]/.dyn1eq,P2[0]/.dyn1eq},{t,-5,0}]]}}]
Out[]=

In[]:=
solution[.1,200,5,.15,.2,.3,.1,.2,.5,0,0,500,.1,.1]
In[]:=
GraphicsGrid[{{fig6B=Plot[{P1[t]/.dyn1,P2[t]/.dyn1},{t,0,60},Ticks->False,PlotRange->All],fig6F=Show[Plot[{P1[t]/.dyn1eq,P2[t]/.dyn1eq},{t,0,50},PlotRange->All,ImageSize->300,AxesOrigin->{-5,0},Ticks->False],Plot[{P1[0]/.dyn1eq,P2[0]/.dyn1eq},{t,-5,0}]]}}]
Out[]=

In[]:=
solution[.1,200,.5,.15,.2,.3,.1,.2,.5,0,0,500,.1,.1]
In[]:=
GraphicsGrid[{{fig6C=Plot[{P1[t]/.dyn1,P2[t]/.dyn1},{t,0,30},Ticks->False,PlotRange->All],fig6G=Show[Plot[{P1[t]/.dyn1eq,P2[t]/.dyn1eq},{t,0,20},PlotRange->All,ImageSize->300,AxesOrigin->{-5,0},Ticks->False],Plot[{P1[0]/.dyn1eq,P2[0]/.dyn1eq},{t,-5,0}]]}}]
Out[]=

In[]:=
solution[.1,500,.2,.15,.2,.3,.1,.2,.5,1,1,200,.1,.1]
In[]:=
fig6D=Show[Plot[{P1[t]/.dyn2,P2[t]/.dyn2},{t,0,60},PlotRange->All],Plot[{P1[t]/.dyn1,P2[t]/.dyn1},{t,0,60},PlotStyle->Dashed,PlotRange->All],PlotRange->All,AxesOrigin->{0,0},PlotRange->All,Ticks->False]
Out[]=

In[]:=
solution[.1,500,10,.2,.2,.3,.2,.2,.5,0,0,200,.1,.1]
In[]:=
fig6H=Show[Plot[{P1[0]/.dyn2eq,P2[0]/.dyn2eq},{t,-5,0},PlotRange->All],Plot[{P1[t]/.dyn2eq,P2[t]/.dyn2eq},{t,0,30},PlotRange->All],Plot[{P1[t]/.dyn1eq,P2[t]/.dyn1eq},{t,0,30},PlotStyle->Dashed,PlotRange->All],PlotRange->All,AxesOrigin->{-5,0},PlotRange->All,Ticks->False]
Out[]=

In[]:=
GraphicsGrid[{{fig6A,fig6B,fig6C,fig6D},{fig6E,fig6F,fig6G,fig6H}},ImageSize->900]
Out[]=

Cite this as: Clemente Arias, "Metabolic overflow prevents ecological collapse in microbial populations" from the Notebook Archive (2025), https://notebookarchive.org/2025-05-0h29lnh
Download
