RTNI - A symbolic integrator for Haar-random tensor networks
Author
Motohisa Fukuda, Robert König, Ion Nechita
Title
RTNI - A symbolic integrator for Haar-random tensor networks
Description
RTNI allows to compute averages of tensor networks containing multiple Haar-distributed random unitary matrices and deterministic symbolic tensors
Category
Working Material
Keywords
tensor networks, random tensors, random unitary matrices, symbolic integration, Weingarten calculus
URL
http://www.notebookarchive.org/2020-01-a42211b/
DOI
https://notebookarchive.org/2020-01-a42211b
Date Added
2020-01-22
Date Last Modified
2020-01-22
File Size
126.15 kilobytes
Supplements
Rights
CC BY 4.0

Examples for the use of RTNI discussed in the paper
Examples for the use of RTNI discussed in the paper
In[]:=
SetDirectory[NotebookDirectory[]];<<RTNI`
Package RTNI (Random Tensor Network Integrator) version 1.0.5 (last modification: 26/01/2019).
Loading precomputed Weingarten Functions from /precomputedWG/functions1.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions2.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions3.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions4.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions5.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions6.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions7.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions8.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions9.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions10.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions11.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions12.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions13.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions14.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions15.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions16.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions17.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions18.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions19.txt
Loading precomputed Weingarten Functions from /precomputedWG/functions20.txt
Example: Creation of Figure 3 in main paper
Example: Creation of Figure 3 in main paper
In[]:=
e1={{"U",1,"out",1},{"U",2,"out",1}}e2={{"U",1,"in",1},{"A",1,"out",1}}e3={{"U",2,"in",1},{"A",1,"out",2}}g={e1,e2,e3};visualizeTN[g]Export["visualizeTNnoedgelabels.pdf",%]visualizeTN[g,{EdgeLabelingTrue}]Export["visualizeTNedgelabels.pdf",%]
Out[]=
{{U,1,out,1},{U,2,out,1}}
Out[]=
{{U,1,in,1},{A,1,out,1}}
Out[]=
{{U,2,in,1},{A,1,out,2}}
Out[]=

Out[]=
visualizeTNnoedgelabels.pdf
Out[]=

Out[]=
visualizeTNedgelabels.pdf
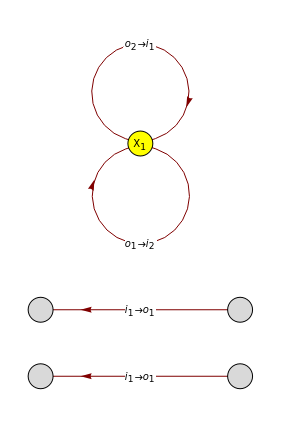
Example 6.1: Twirling a matrix
Example 6.1: Twirling a matrix
In[]:=
e1={{"U",1,"out",1},{"X",1,"in",1}};e2={{"Y",1,"out",1},{"U",1,"in",1}};e3={{"U*",1,"out",1},{"Y",1,"in",1}};e4={{"X",1,"out",1},{"U*",1,"in",1}};g={e1,e2,e3,e4}visualizeTN[g](*alternative:visualizeTN[{{g,1}},{EdgeLabelingTrue}]*)Export["TrXUYUstar.pdf",%]Eg=integrateHaarUnitary[g,"U",{d},{d},d];visualizeTN[Eg]Export["ETrXUYUstar.pdf",%]
Out[]=
{{{U,1,out,1},{X,1,in,1}},{{Y,1,out,1},{U,1,in,1}},{{U*,1,out,1},{Y,1,in,1}},{{X,1,out,1},{U*,1,in,1}}}
Out[]=

Out[]=
TrXUYUstar.pdf
Out[]=
 ,
,

1
d
Out[]=
ETrXUYUstar.pdf
In[]:=
e1={{"U",1,"out",1},{"X",1,"in",1}};e2={{"Y",1,"out",1},{"U",1,"in",1}};e3={{"U*",1,"out",1},{"Y",1,"in",1}};g={e1,e2,e3}Eg=integrateHaarUnitary[g,"U",{d},{d},d]visualizeTN[g]Export["XUYUstar.pdf",%]visualizeTN[Eg]Export["EXUYUstar.pdf",%]
Out[]=
{{{U,1,out,1},{X,1,in,1}},{{Y,1,out,1},{U,1,in,1}},{{U*,1,out,1},{Y,1,in,1}}}
Out[]=
{{{Y,1,out,1},{Y,1,in,1}},{{X,1,in,1},{dummy-U*-IN-1-1,1,out,1}}},
1
d
Out[]=

Out[]=
XUYUstar.pdf
Out[]=
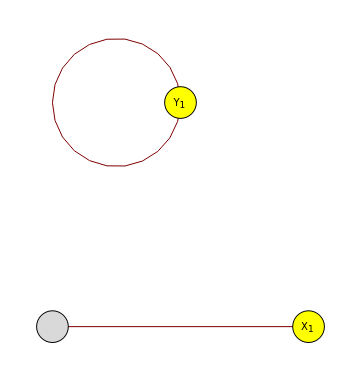 ,
,

1
d
Out[]=
EXUYUstar.pdf
Example 6.2: Several tensor factors
Example 6.2: Several tensor factors
In[]:=
e1={{"A",1,"out",1},{"U",1,"in",1}};e2={{"A",1,"out",2},{"U",1,"in",2}};e3={{"U*",1,"out",1},{"A",1,"in",1}};e4={{"U*",1,"out",2},{"A",1,"in",2}};e5={{"U",1,"out",2},{"U*",1,"in",2}};g={e1,e2,e3,e4,e5}Eg=integrateHaarUnitary[g,"U",{n,k},{n,k},nk]visualizeTN[g]Export["id-Tr-UU-A-UstarUstar.pdf",%]visualizeTN[Eg]Export["E-id-Tr-UU-A-UstarUstar.pdf",%]
Out[]=
{{{A,1,out,1},{U,1,in,1}},{{A,1,out,2},{U,1,in,2}},{{U*,1,out,1},{A,1,in,1}},{{U*,1,out,2},{A,1,in,2}},{{U,1,out,2},{U*,1,in,2}}}
Out[]=
{{{A,1,out,1},{A,1,in,1}},{{A,1,out,2},{A,1,in,2}},{{dummy-U-OUT-1-1,1,in,1},{dummy-U*-IN-1-1,1,out,1}}},
1
n
Out[]=

Out[]=
id-Tr-UU-A-UstarUstar.pdf
Out[]=
 ,
,

1
n
Out[]=
E-id-Tr-UU-A-UstarUstar.pdf
Example 6.3: Bi-partite twirling
Example 6.3: Bi-partite twirling
In[]:=
e1={{"X",1,"out",1},{"U",1,"in",1}};e2={{"U*",1,"out",1},{"X",1,"in",1}};e3={{"X",1,"out",2},{"U",2,"in",1}};e4={{"U*",2,"out",1},{"X",1,"in",2}};g={e1,e2,e3,e4}visualizeTN[g]Export["twirl.pdf",%]integrateHaarUnitary[g,"U",{d},{d},d]visualizeTN[%,EdgeLabelingTrue]Export["E-twirl.pdf",%]
Out[]=
{{{X,1,out,1},{U,1,in,1}},{{U*,1,out,1},{X,1,in,1}},{{X,1,out,2},{U,2,in,1}},{{U*,2,out,1},{X,1,in,2}}}
Out[]=
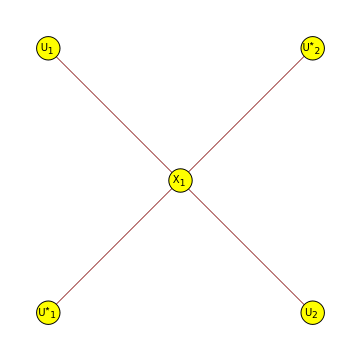
Out[]=
twirl.pdf
Out[]=
{{{X,1,out,1},{X,1,in,1}},{{X,1,out,2},{X,1,in,2}},{{dummy-U-OUT-1-1,1,in,1},{dummy-U*-IN-1-1,1,out,1}},{{dummy-U-OUT-2-1,1,in,1},{dummy-U*-IN-2-1,1,out,1}}},,{{{X,1,out,1},{X,1,in,1}},{{X,1,out,2},{X,1,in,2}},{{dummy-U-OUT-1-1,1,in,1},{dummy-U*-IN-2-1,1,out,1}},{{dummy-U-OUT-2-1,1,in,1},{dummy-U*-IN-1-1,1,out,1}}},,{{{X,1,out,1},{X,1,in,2}},{{X,1,out,2},{X,1,in,1}},{{dummy-U-OUT-1-1,1,in,1},{dummy-U*-IN-1-1,1,out,1}},{{dummy-U-OUT-2-1,1,in,1},{dummy-U*-IN-2-1,1,out,1}}},,{{{X,1,out,1},{X,1,in,2}},{{X,1,out,2},{X,1,in,1}},{{dummy-U-OUT-1-1,1,in,1},{dummy-U*-IN-2-1,1,out,1}},{{dummy-U-OUT-2-1,1,in,1},{dummy-U*-IN-1-1,1,out,1}}},
1
-1+
2
d
1
d-
3
d
1
d-
3
d
1
-1+
2
d
Out[]=
 ,,
,, ,,
,, ,,
,, ,
,

1
-1+
2
d

1
d-
3
d

1
d-
3
d

1
-1+
2
d
Out[]=
E-twirl.pdf
Example 6.4: Bell state as input in conjugate random quantum channels
Example 6.4: Bell state as input in conjugate random quantum channels
In[]:=
e1={{"U*",2,"out",1},{"U",1,"in",1}};e2={{"U*",1,"out",1},{"U",2,"in",1}};e3={{"U",1,"out",1},{"U*",1,"in",1}};e4={{"U",2,"out",1},{"U*",2,"in",1}};e5={{"U",1,"out",2},{"U*",2,"in",2}};e6={{"U",2,"out",2},{"U*",1,"in",2}};g={e1,e2,e3,e4,e5,e6};listg={{g,1/(dk)}};Eg=integrateHaarUnitary[listg,"U",{d},{n,k},nk]overlap=Eg[[1,2]];overlapt=overlap/.{dtnk};Assuming[t>0&&k>1,Limit[overlapt,nInfinity]]//Simplify
Out[]=
{},-n-++k
2
d
2
k
dk-d
3
k
2
n
dk
2
n
dk-d
3
k
2
n
dn
2
k
dn-d
2
k
4
k
3
n
2
d
2
n
dn-d
2
k
4
k
3
n
Out[]=
1-t
2
k
Example 6.5: Random tensor networks for holographic duality
Example 6.5: Random tensor networks for holographic duality
In[]:=
(*seeseparatefileexamples_holographictensornetworks*)
In[]:=
Example 6.6: Computation of expectation values of matrix products
Example 6.6: Computation of expectation values of matrix products
In[]:=
MultinomialexpectationvalueHaar[d,{1,2},{X,Y},True]
Out[]=
Tr[X]Tr[Y]
d
In[]:=
MultinomialexpectationvalueHaar[d,{1,3},{X,Y},False]
Out[]=
0
In[]:=
MultinomialexpectationvalueHaar[d,{2,3},{X,Y},False]
Out[]=
X.Transpose[Y]
d
In[]:=
MultinomialexpectationvalueHaar[d,{1,4},{X,Y},True]
Out[]=
Tr[X.Transpose[Y]]
d
In[]:=
MultinomialexpectationvalueHaar[d,{1,2,3,4},{V,W,X,Y},False]
Out[]=
V.Transpose[Y].X.Transpose[W]
-1+
2
d
V.Transpose[Y].XTr[W]
d-
3
d
V.X.Transpose[W]Tr[Y]
d-
3
d
V.XTr[W]Tr[Y]
-1+
2
d
In[]:=
(*foradditionalexamplesfortheuseofMultinomialexpectationvalueHaar,seefileexamples_momentcalculator.nb*)
Cite this as: Motohisa Fukuda, Robert König, Ion Nechita, "RTNI - A symbolic integrator for Haar-random tensor networks" from the Notebook Archive (2019), https://notebookarchive.org/2020-01-a42211b
Download
